关于一个半离散非齐次核的逆向Hilbert型不等式＊

谢子填，孙宇锋

（1.韶关学院，广东韶关 512005；2.广东肇庆学院数学与信息科学学院，广东肇庆 526061）

关于一个半离散非齐次核的逆向Hilbert型不等式＊

谢子填1，2，孙宇锋1

（1.韶关学院，广东韶关 512005；2.广东肇庆学院数学与信息科学学院，广东肇庆 526061）

应用权函数方法及实分析技巧，给出一个新的带有最佳常数因子的半离散非齐次核的逆向Hilbert型不等式，同时给出它的带有最佳常数因子的等价式.

半离散；Hilbert不等式；Holder不等式；等价式

近年来，人们陆续对不等式（1）和（2）作了大量推广［2－15］.笔者应用权函数，将给出一个带有最佳常数因子的半离散非齐次核的逆向Hilbert型不等式，同时给出它的等价式.

引理1 定义权系数及权函数

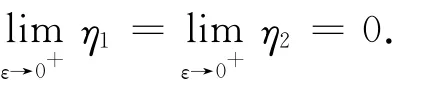
由（13）和（14）式，有K＋η1＋η2≥H（ε＋1.令ε→0＋，有K≥H与假设K＜H矛盾.可知K确为（8）式最佳值.

注意到（8），（9）和（10）式等价，易知式（9）和（10）式的常数因子也必为最佳值.

［1］ HARDY G H.Note on a Theorem of Hilbert Concerning Series of Positive Term［J］.Proc.London Math.Soc.，1925，23（2）：XLV－XLVI.

［2］ 杨必成.一个半离散的Hilbert不等式［J］.广东第二师范学院学报，2011，31（3）：1－7.

［3］ 杨必成.一个推广的非齐次核的Hilbert型积分不等式［J］.吉林大学学报：理学版，2010，48（5）：719－722.

［4］ XUE Zi-tian，ZENG Zheng.A Hilbert-Type Integral Inequality Whose Kernel is a Homogeneous Form of Degree-3［J］.J.Math.Anal.Appl.，2008，339：324－331.

［5］ 曾 峥，谢子填.一个新的有最佳常数因子的Hilbert型积分不等式［J］.华南师范大学学报：自然科学版，2010（3）：31－33.

［6］ ZENG Zheng，XIE Zi-tian.A Hilbert’s Inequality with a Best Constant Factor［J］.Journal of Inequalities and Applications，2009，Article ID 820176，8Pages，doi：10.1155／2009／820176.

［7］ ZENG Zheng，XIE Zi-tian.On a New Hilbert-Type Integral Inequality with the Integral in Whole Plane［J］.Journal of Inequalities and Applications，2010，Article ID 256796，8Pages，2010.doi：10.1155／2010／256796.

［8］ XIE Zi-tian，ZENG Zheng.A New Hilbert-Type Inequality with the Integral in Whole Plane［J］.Kyungpook Mathematical Journal，2012，52：291－298.

［9］ XIE Zi-tian.A New Reverse Hilbert-Type Inequality with a Best Constant Factor［J］.J.Math.Anal.Appl.，2008，343：1 154－1 160.

［10］ 谢子填，杨必成，曾 峥.一个新的实齐次核的Hilbert型积分不等式［J］.吉林大学学报：理学版，2010，48（6）：941－945.

［11］ 谢子填，曾 峥.一个实齐次核的Hilbert型积分不等式及其等价形式［J］.浙江大学学报：理学版，2011，38（3）：266－270.

［12］ 谢子填.一个实数齐次核的Hilbert型积分不等式［J］.吉首大学学报：自然科学版，2011，32（4）：26－30.

［13］ 谢子填，曾 峥.一个新的－4μ齐次半离散Hilbert型不等式［J］.吉首大学学报：自然科学版，2012，33（3）：15－19.

［14］ XIE Zi-tian，ZENG Zheng.On a Hilbert-Type Integral Inequality with the Homogeneous Kernel of Real Number-Degree and Its Operator Form［J］.Advances and Applications in Mathematical Sciens，2011，10（5）：481－490.

［15］ XIE Zi-tian，ZENG Zheng.A New Hilbert-Type Inequality in Whole Plane with the Homogeneous Kernel of Degree 0［J］.i-Manager’s Journal on Mathematics，2013，2（1）：13－19.

［16］ 匡继昌.常用不等式［M］.第3版.济南：山东科技出版社，2004.

（责任编辑 向阳洁）

On a Half-Discrete Reverse Hilbert-Type Inequality with a Non-Homogeneous Kernel

XIE Zi-tian1，2，SUN Yu-feng1
（1.Shaoguan University，Shaoguan 512005，Guangdong China；2.School Mathematics and Information Sciences，Zhaoqing University，Zhaoqing 526061，Guangdong China）

By using the way of weight functions，a new half-discrete reverse Hilbert-type inequality is giver，with a non-homogeneous kernel and with a best constant factor.An equivalent form with a best constant factor is presented.

half-discrete；Hilbert-type inequality；Hölder’s inequality；equality form

O178

A

10.3969／j.issn.1007－2985.2013.05.004

1007－2985（2013）05－0011－05

2013－02－09

广东省自然科学基金资助项目（S2012010010069）

谢子填（1948－），男，广东肇庆人，广东肇庆学院数学与信息科学学院教授，主要从事解析不等式研究.