无损链码技术的分析与比较
李灵华,刘勇奎
(大连民族学院 计算机科学与工程学院,辽宁 大连116600)
0 引 言
链码由于其使用简单方便,占用存储空间少而被广泛应用于图像处理、模式识别、形状分析等各领域。随着图形图像处理各领域对链码越来越多的应用,链码技术也得到了快速的发展,许多不同的链码新方法被提了出来。根据在描述的过程中对形状信息的丢失与否,链码可分为有损压缩、准无损压缩和无损压缩。本文选取典型的无损压缩链码方法,进行深入的分析和比较,并通过实验给出对各链码方法的评价,针对各链码技术的特点,剖析了其形成的原因。
1 无损链码技术研究
可以从两个方面来讨论链码技术,分别是:基于像素的链码技术和基于边界的链码技术。对于基于像素的链码技术,本文主要介绍典型的Freeman链码技术;对于基于边界的链码技术,本文主要介绍顶点链码技术。
1.1 Freeman链码
一些典型的Freeman链码包括:8方向Freeman、4方向Freeman链码、角度差Freeman链码、直角变化3方向Freeman链码、改进的相对8方向Freeman链码、以及应用计算编码的直角变化3方向Freeman链码,等等。
1.1.1 8方向Freeman链码和4方向Freeman链码
1961年,Freeman提出的8方向Freeman链码D8FCC(8-direction Freeman chain code)是所有链码技术研究的基础。另一种较为常用的是4方向Freeman链码D4FCC(4-direction Freeman chain code)。
D8FCC和D4FCC的链码编码简单,但二者都不独立于旋转操作,即在旋转操作下链码改变。
1.1.2 角度差 Freeman链码
2005年,刘勇奎等提出角度差Freeman链码ADFCC(angle differences Freeman chain code)[1]。在 ADFCC 中,第一个码值仍然采用D8FCC链码,其余每个码值则采用它与其前一个码值的相对角度差进行编码。ADFCC基于最常用的D8FCC和霍夫曼 (Huffman)编码思想,编码时考虑到各码值出现的不同概率。
ADFCC的码值有8个,即ADFCC∈ {C0,C1,C2,C3,C4,C5,C6,C7}。D8FCC、D4FCC和 ADFCC编码实验结果表明ADFCC的总码长与D8FCC相同,为最短码长。并且,ADFCC的平均码长最短,存储所需二进制位数最少,相对比率最小。同时,ADFCC独立于旋转操作,即在旋转操作下链码不变。
1.1.3 直角变化3方向Freeman链码
2005年,H.Sánchez-Cruz等人提出了直角3方向Freeman 链 码 3OT (orthogonal three-direction Freeman chain code)[2]。3OT中有3个码:0、1、2,其基于3种相对变化的直角方向。码0表示没有方向变化,即沿着前一个码前进的方向 “直行”;码1表示参照之前行走的方向的变化趋势是 “向前行进”;码2表示参照之前行走的方向的变化趋势是 “向后回转”。为了将码值0、1、2进行数字化表示,采用Huffman编码方法编码为二进制码。
3OT的码值有3个,即3OT∈ {0,1,2},其平均码长为1.51位/码,3OT 独立于旋转操作[2]。在文献 [2]中,作者还给出了基于35幅图像的D8FCC、D4FCC、ADFCC及3OT编码实验结果对比,实验结果表明在参与比较的所有链码中,D8FCC和ADFCC的总码长最短,且D8FCC的效率最低,ADFCC的效率最高。
1.1.4 改进的相对8方向Freeman链码
2007年,S.Zahir等人基于8方向Freeman链码和角度差Freeman链码提出了改进的相对8方向Freeman链码ERD8FCC (enhanced relative 8-direction Freeman chain code)[3]。
ERD8FCC在D8FCC的基础上,变绝对的8方向运动为相对的8方向变化,同时引入了 (n10,5)规则以提高压缩率,同时也采用Huffman编码方法实现不等长编码。
ERD8FCC的码值共有10个,分别是F(前方)、FR(右前方)、FL (左前方)、R (右方)、L (左方)、BR (右后方)、BL(左后方)、B (后方)、Y (5个连续的前方)以及X (10个连续的前方)。
由于文献 [3]中并未给出每个码值的Huffman编码的二进制位码形式,因此,在后面的实验比较中,我们将基于10幅实验图像的统计给出Huffman编码结果。
ERD8FCC的码值有10个,即ERD8FCC∈ {F,FR,FL,R,L,BR,BL,B,Y,X},ERD8FCC独立于旋转操作。在文献 [3]中,ERD8FCC被用于形状及二值图像的压缩与复原中,该文作者对46幅二值图像的D8FCC、D4FCC、ADFCC及ERD8FCC编码实验结果对比,实验结果表明在参与比较的所有链码中,ERD8FCC效率最高[3]。
1.1.5 应用计算编码的直角变化3方向Freeman链码
2009年,H.Sánchez-Cruz等人在3OT的基础上加入了计算编码,提出了基于计算编码的直角变化3方向Freeman链 码 Arith_3OT (arithmetic coding applied to 3OT chain code)[4]。除了3OT中的3个码值0、1、2外,Arith_3OT中增加了3个码值3、4、5。码值0、1、2所表示的含义与3OT中的定义相同。码值3表示每5个连续的符号0的情况,码值4表示每5个连续的符号1的情况,码值5表示符号组合0110的情况。
由于文献 [4]中同样并未给出每个码值的Huffman编码的二进制位码形式,因此,在后面的实验比较中,我们也将基于10幅实验图像的统计给出Arith_3OT的Huffman编码结果。
Arith_3OT的码值有6个,即Arith_3OT∈ {0,1,2,3,4,5},Arith_3OT独立于旋转操作。在文献 [4]中,Arith_3OT被应用于二值图像的轮廓形状编码中,该文作者对16幅二值图像的ADFCC及Arith_3OT编码实验结果对比,实验结果表明Arith_3OT的效率最高[4]。
1.2 顶点链码
一些典型的顶点链码包括:原始顶点链码、扩展顶点链码、变长顶点链码,变长压缩顶点链码、动态顶点链码、以及等长压缩顶点链码,等等。
1.2.1 原始顶点链码
1999年,E.Bribiesca首先介绍了顶点链码的概念,此为原始顶点链码VCC(vertex chain code)。顶点链码是基于形状边界的顶点像素的数目进行编码的。
在顶点链码中,任意形状的边界或轮廓是由规律排列的单元组成的。因此,顶点链码描述的是封闭的边界。最小的封闭边界只包含一个像素。VCC中的每个码的码值表示该顶点是几个边界像素的顶点,对应用3个码值0、1、2分别表示该顶点是0、1、2这3个边界像素的顶点。
VCC的码值有3个,即VCC∈ {1,2,3},其平均码长为2位/码。VCC独立于旋转操作。
在文献 [5]中,VCC被用于表示图像区域,在文献[6]和文献 [7]中,顶点链码被用于曲线长度估计,在文献 [8]中,其被用于提取目标图像的最小外接矩形。
1.2.2 扩展顶点链码
2007年,文献 [9]基于原始顶点链码提出了一种改进的顶点链码,称为扩展顶点链码E_VCC(extended vertex chain code)。
VCC是等长编码,码长为二位二进制数,用来表示码值1、2和3。但是,二位二进制数是可以对四个码值进行编码表示的。E_VCC在不增加码长的情况下,增加一个码值0,用来表示在图像边界上最经常出现的角点相邻的情况,即码值1和3组合的情况。
E_VCC比VCC所用的数据少。E_VCC的码值有4个,即VCC∈ {0,1,2,3},其平均码长为2位/码。E_VCC独立于旋转操作[9]。
1.2.3 变长顶点链码
在文献 [9]中,作者还基于原始顶点链码提出了第二种改进的顶点链码,称为变长顶点链码V_VCC(variablelength vertex chain code)。
V_VCC仍采用VCC的3个码值1、2和3。所不同的是,V_VCC考虑到这三种码值的出现概率。统计结果表明,码值2的出现概率远大于另两个码值。因此,V_VCC用1位二进制位0编码码值2,码值1和码值3则分别用2位二进制位10和11进行编码。
V_VCC的功能与VCC相同,但其长度要远远小于VC的长度。V_VCC的码值有3个,即VCC∈ {1,2,3},其平均码长为1.49位/码,V_VCC独立于旋转操作[9]。
1.2.4 变长压缩顶点链码
文献 [9]中,作者还基于原始顶点链码及Huffman编码思想提出了第三种改进的顶点链码,称为变长压缩顶点链 码 VC _VCC (variable-length compressed vertex chain code)。
VC_VCC考虑到各码值的出现概率,将E_VCC与V_VCC相结合而成。它包括5个码值,分别是码值1、码值2、码值3、码值4和码值5。新增加的两个码值分别用于表示两种组合情况,即 “1和3组合”和 “3和1组合”。5个码值按出现概率采用Huffman编码为二进制码。
当轮廓边界越长时,采用VC_VCC的节省数据位数的优势越明显。VC_VCC的码值有5个,即VC_VCC∈{c1,c2,c3,c4,c5},其平均码长为1.62位/码,VC_VCC独立于旋转操作[9]。
文献 [10]在VC_VCC的基础上提出了分段编码的思想,从而得到更高的数据压缩率。
1.2.5 动态顶点链码
2010年,于国防等人基于原始顶点链码提出了一种改进的顶点链码,称为动态顶点链码D_VCC(dynamic vertex chain code)[11]。
D_VCC的思想是改变VCC中各码值直观表示顶点像素的数目的含义,对链码组成元素重新分配码值。即以十进制数值0(或9)表示原码值1,以十进制数值9(或0)表示原码值3,而以十进制数值18动态且直观地表示原码值2及码值2连续出现的个数。
从文献 [11]的描述中可以看出,D_VCC码值有10个,即D_VCC∈ {0,1,2,3,4,5,6,7,8,9},平均码长则为4位/码,其在减少链码总码数的同时却增加了码值的二进制位数。D_VCC主要追求的是在总码数方面的高压缩率而未考虑链码占用的存储空间 (总二进制位数)的大小。
1.2.6 等长压缩顶点链码
文献 [11]中,作者还基于上述的VCC和E_VCC提出了一种新的压缩顶点链码,称为等长压缩顶点链码EC_VCC (equivalent-length compressed vertex chain code)。
EC_VCC改变以往链码以位 (bit)为最小单位的存储方式,而采用以字节 (byte)为最小单位的存储方式。EC_VCC的基本思想是将一个字节 (8位二进制数)拆分为高2位和低6位两部分。高2位的编码用于表示EC_VCC的码值,第6位的编码用于表示高2位指定的码值连续出现的个数。2位二进制编码最多可表示4种码值,6位二进制编码最多可表示码值连续出现的个数是64个。如果码值连续出现的个数超过64个,则开始一个新的字节编码。
EC_VCC同样追求的是在总码数方面的高压缩率而未考虑链码占用的存储空间 (总二进制位数)的大小。EC_VCC采用等长编码,其码值最多可有256个,码长为8位/码。文献 [11]对3幅图像的D8FCC、D4FCC、VCC、VC_VCC、D_VCC以及EC_VCC编码实验结果进行对比,实验结果表明在参与比较的所有链码中,VC_VCC具有稳定高效的编码压缩比,而D_VCC和EC_VCC的压缩比随图像形状的变化而变化,图像中包含的连续同向走线越多,压缩比就越高[11]。
2 比较与评价
2.1 链码的评价方法
文献 [9]中给出了评价链码效率的公式如下

式中:E——链码的效率,C——码值平 均表达能力,L——平均码长。也就是说,一种链码的效率与其码值平均表达能力成正比,与其平均码长成反比,其含义是每个二进制位平均所表示的边界的长度。
链码的码值平均表达能力C指的是该链码的各码值所能表示的区域边界 (或数字曲线)的长度的平均值,以像素单位作为计量单位。例如,当一个码值表示的是边相邻像素间的接续关系时,如D8FCC的码值0、2、4和6,则C为1;当它表示的是角点相邻像素间的接续关系时,如D8FCC的码值1、3、5和7,则C为2。
2.2 链码的比较
我们分别从两个方面对文中提到的链码方法进行比较:实验结果和理论分析。
2.2.1 实验结果比较
我们选取实际图像中10个景物的轮廓进行实验,如图1所示。轮廓图像的尺寸列于表1中。

图1 实验图像
针对图1中10幅实验图像的轮廓,我们分别采用文中提到的6种Freeman链码及6种顶点链码进行编码,分别统计每幅图像轮廓链码的总长度,即链码的总码数如表2所示。
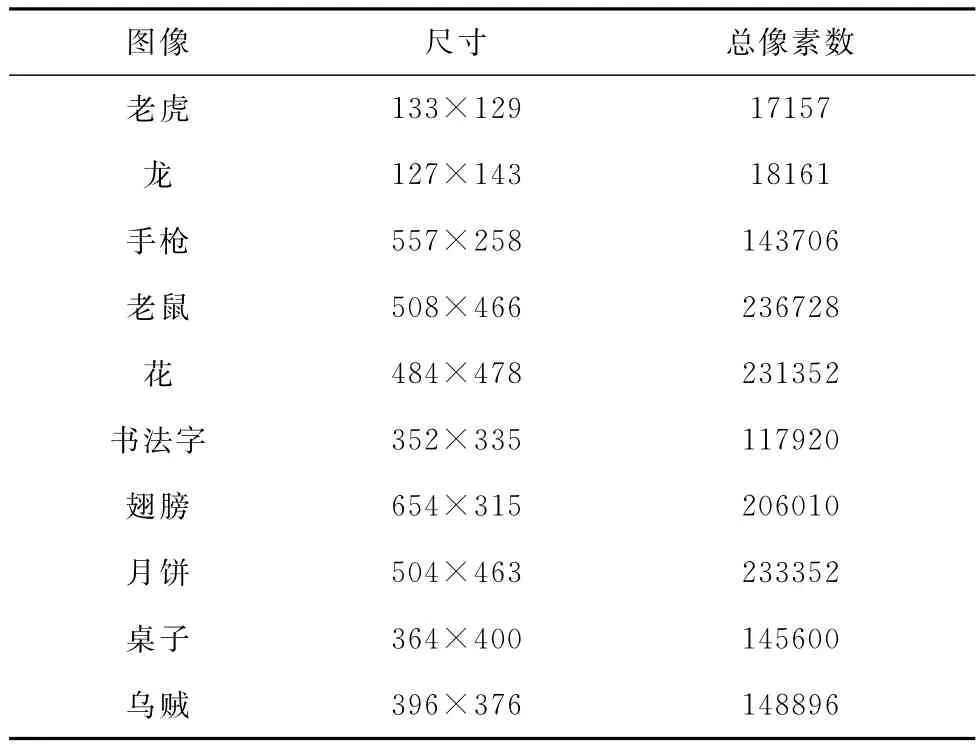
表1 实验图像尺寸列表

表2 实验图像采用不同链码方法得到的链码总长度 (链码总码数)

表3 不同链码的码值数及每位编码需要的二进制位数 (位/码)
文中提到的6种Freeman链码及6种顶点链码的码值数及每码编码需要的二进制位数 (位/码)列于表3中。
在12种链码中,有6种链码采用不等长编码。其中ADFCC、3OT、V_VCC和VC_VCC链码的每个码值对应的二进制编码分别见文献 [1]、文献 [2]以及文献 [9],ERD8FCC和Arith_3OT链码的每个码值对应的二进制编码我们通过对表2中10幅实验图像的ERD8FCC和Arith_3OT各码值出现的概率分别进行统计,并进行Huffman编码,得到的编码结果分别见表4和表5。

表4 ERD8FCC各码值的出现概率及二进制编码

表5 Arith_3OT各码值的出现概率及二进制编码
这样,我们通过计算得到文中提到的6种Freeman链码及6种顶点链码对10幅实验图像分别进行编码所占用的存储空间大小,用所需二进制总位数进行衡量,见表6。
通过对表2中得到的针对10幅实验图像的12种链码的总码数和表6中的二进制总位数的计算,得到12种链码的平均码长列于表7中。

表6 实验图像采用不同链码方法编码所占存储空间大小 (二进制总位数)

表7 文中提及的12种链码的平均码长 (位/码)
分析文中提到的12种链码,对于D4FCC、3OT、VCC、V_VCC这4种链码,由于每个码值表示的都为边相邻像素间的接续关系,每个码值的表达能力都为1,因此,码值的平均表达能力为1。
对于D8FCC、ADFCC、E_VCC、VC_VCC这4种链码,分别有表示边相邻像素和角点相邻像素间的接续关系的码值,D8FCC和ADFCC中的两种情况的码值出现概率是相同的。基于上述10幅实验图像,分别统计码值表达能力为1和2的码值出现概率,从而计算出该4种链码的码值平均表达能力。
对于ERD8FCC、Arith_3OT、D_VCC、EC_VCC这4种链码,分别有表示边相邻像素和角点相邻像素间的接续关系的码值,同时,因为链码中采用了计算编码,所以,有些码值描述的是多个像素。如ERD8FCC中的码值Y的表达能力为5,码值X的表达能力为10;Arith_3OT中的码值3和4的表达能力为5,码值5的表达能力为4;D_VCC中码值28的表达能力分别为28;EC_VCC中码值的表达能力最多可达到64。基于上述10幅实验图像,分别统计4种链码中不同码值表达能力的码值的出现概率,从而计算出该4种链码的码值平均表达能力。
12种链码的码值数、码值、码值表达能力、不同表达能力码值出现的概率、以及平均表达能力的计算结果列于表8中。
考虑到EC_VCC链码的码值较多,并且对应的每个码的码值表达能力各不相同,因此,表8中没有分别列出EC_VCC的所有码值、各个码值的表达能力以及出现的概率统计,在出现概率统计一栏中给出的数字1.000指的是将所有码值放在一起。最后给出了平均表达能力的计算结果值,这一结果同样是基于10幅实验图像,采用与其他链码相同的统计方法获得,只不过这个计算量要比其他的大很多。
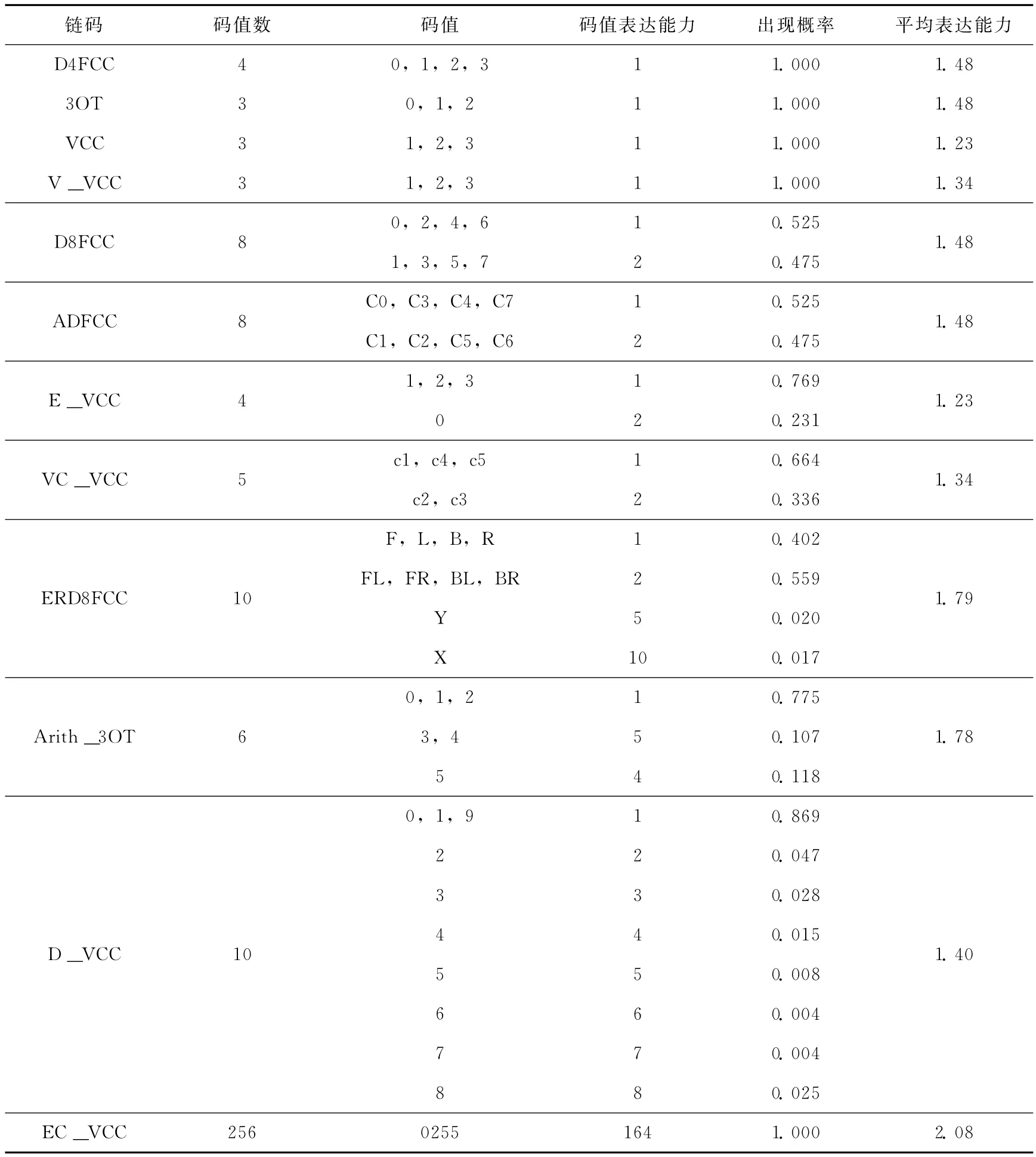
表8 文中12种链码的码值数、码值、码值表达能力、出现概率及平均表达能力
综合上述分析及得到的数据,我们通过计算得到12种链码效率的相关结果,见表9。
2.2.2 理论分析比较
由表2可以看出,12种链码中链码总长度最短的是EC_VCC,为14241个码,接下来的是Arith_3OT,为16828个码,以及ERD8FCC,为17701个码。12种链码中链码总长度最长的是VCC和V_VCC,都为29600个码,接下来的是D4FCC和3OT,都为29560个码,其他链码的链码总长度处于中等。
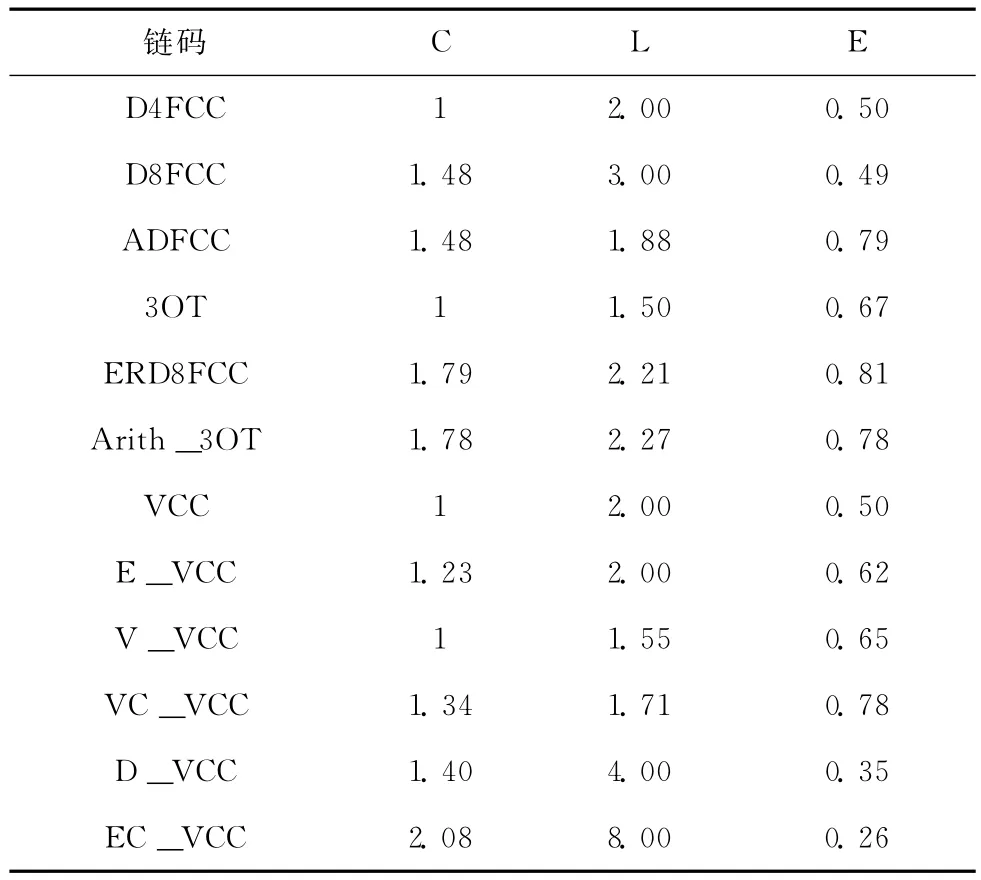
表9 文中提及的12种链码的效率
可见,EC_VCC实现了其所追求的目标,即链码总长度最短。其采用的方法是变按位为最小存储单位为按字节为最小存储单位,并采用等长编码及行程编码,该方法对于目标的实现是有效的。同时,由表3可见,EC_VCC使用的码值最多,而VCC和V_VCC使用的码值最少。因此,要想缩短链码总长度,就要增加链码的码值数。
由表6可以看出,12种链码中链码编码所占存储空间最小的是VC_VCC,为38000位二进制码,接下来的是Arith_3OT,为38293位二进制码,以及ERD8FCC,为39121位二进制码。12种链码中链码编码所占存储空间最大的是EC_VCC,为113928位二进制码,接下来的是D_VCC,为89240位二进制码,其他链码编码所占存储空间处于中等。
分析这一结果形成的原因,VC_VCC、Arith_3OT和ERD8FCC都采用变长编码,编码时考虑码值出现的概率,应用了Huffman编码思想。所占存储空间最小的VC_VCC还采用的组合编码的码值,这也是进一步减少链码编码存储空间的有效措施。反之,所占存储空间最大的EC_VCC和次大的D_VCC都采用等长编码,编码时未考虑码值出现的概率。
由表7可以看出,12种链码中平均码长最短的是3OT,为1.50位/码,接下来的是V_VCC,为1.55位/码,以及VC_VCC,为1.71位/码。12种链码中平均码长最长的是EC_VCC,为8位/码,接下来的是D_VCC,为4位/码,其他链码平均码长处于中等。
由表8可以看出,12种链码中码值平均表达能力最强的是EC_VCC,为2.08像素单位,接下来的是ERD8FCC,为1.79像素单位,以及Arith_3OT,为1.78像素单位。12种链码中平均表达能力最弱的是VCC和E_VCC,都为1.23像素单位,接下来的是V_VCC和VC_VCC,都为1.34像素单位,其他链码码值平均表达能力处于中等。
由表9可以看出,12种链码中效率最高的是ERD8FCC,为0.81,接下来的是ADFCC,为0.79,Arith_3OT和VC_VCC的效率都为0.78,此4种链码的效率较为相当。12种链码中效率最低的是EC_VCC,仅为0.26,接下来的是D_VCC,为0.35,其他效率处于中等。
可见,虽然EC_VCC的链码表达能力最强,但其平均码长最长,因此,其效率反而最低。ERD8FCC的链码表达能力较强,其平均码长为中等,其效率却为最高。VC_VCC的链码表达能力较弱,其平均码长较短,其效率却为较高。可见,链码效率受平均码长影响的程度要大于受链码表达能力影响的程度。因此,要提高链码的效率,可考虑提高链码的表达能力,但不能以牺牲链码平均码长为代价。
进一步分析这一结果形成的原因,效率高的4种链码均采用了Huffman不等长编码,因而形成了最佳编码。效率最高的ERD8FCC链码不仅采用Huffman编码,还采用了计算编码,虽然在ADFCC的基础上增加了2个码值,但仍得到了最高的链码效率。而效率低的2种链码EC_VCC和D_VCC都采用等长编码,并且在编码的过程中都有冗余。如D_VCC用4位二进制位编码10个码值,冗余了6个编码;EC_VCC则分别采用64个码值编码顶点链码的码值1(二进制编码01b5b4b3b2b1b0)和码值3(二进制编码11b5b4b3b2b1b0),而很显然,码值1和码值3最多只能连续出现2个,因此,各自最多需要的码值是2个,由此产生了2个62个码 (即124个码)的冗余。这样导致了链码EC_VCC和D_VCC的低效率。
链码所占存储空间的大小表明了链码的压缩率,存储空间越小,其压缩率越高。从上述比较结果可见,压缩率高的VC_VCC、Arith_3OT以及ERD8FCC的效率也高,而压缩率低的EC_VCC和D_VCC的效率也低。这也说明了链码的效率是链码压缩率的有力体现。
3 链码技术展望
从文中前面部分的叙述可以看出,链码技术在图像处理以及模式识别领域得到了快速的发展,出现了许多链码的应用及新方法。然而,链码技术的发展最多的都是基于Freeman链码以及顶点链码方法。为了提高链码的压缩率,可以考虑采取不等长编码、计算编码、组合码值编码等措施,将不同链码技术采用的方法结合应用到现有的某一链码中,从而形成新的链码方法。
上述介绍的链码方法都是应用到二维坐标系统描述的图像中,从而将其转化为一维的形式。新的发展趋势则是研究将三维坐标系统描述的图像转化为一维形式的链码技术。另一方面,目前的链码技术都是用于描述简单图像,进一步的发展可以考虑如何将链码技术应用于复杂图像的描述的新方法。
4 结束语
应该指出,介绍的12种链码并不是链码方法的全部。介绍了6种基于像素的链码方法和6种基于边界的链码方法。基于像素的链码方法介绍了Freeman链码,基于边界的链码方法介绍了顶点链码。当然,除了这两类技术外,还有其他基于像素的链码和基于边界的链码技术。
链码之所以成为近年来研究的热点,主要原因在于其高压缩率以及节省存储空间。文中分别从各链码的产生、实现的主要思想、各链码的主要特性及一些典型的应用进行了详细的论述,并结合链码的评价方法对各链码进行了实验结果的比较与理论比较分析,希望本文的研究能为链码的应用者与研究者提供便利与参考。进一步的研究将着眼于选取和确定新的链码码值,将Huffman编码和计算编码相结合,探讨有利于提高链码效率的新方法,这将是我们下一步研究工作的重点。
:
[1]LIU Y K,Zalik B,WANG P J,et al.Directional difference chain codes with quasi-lossless compression and run-length encoding[J].Signal Processing:Image Communication,2012,27(9):973-984.
[2]Sánchez Cruz H,Bribiesca E,Rodríguez Díaz M A.Efficiency of chain codes to represent binary objects[J].Pattern Recognition,2007,40 (6):1660-1674.
[3]Zahir S,Dhou K.A new chain coding based method for binary image compression and reconstruction[J].Picture Coding Symposium,Lisbon,Portugal,2007:1321-1324.
[4]Sánchez Cruz H,Rodríguez Díaz M A.Coding long contour shapes of binary objects[G].LNCS 5856:Progress in Pattern Recognition,Image Analysis,Computer Vision,and Applications,2009:45-52.
[5]YU Youyang,CHEN Youguang,GU Guoqing.Filling algorithm for vertex chain code image[J].Computer Engineering,2008,34 (12):265-267 (in Chinese). [于游洋,陈优广,顾国庆.顶点链编码图像的填充算法 [J].计算机工程,2008,34(12):265-267.]
[6]Dianat O,Haron H.Algorithm for length estimation based on the vertex chain code [C]//Singapore:International Conference on Signal Processing Systems,2009:951-954.
[7]Haron H,Rehman A,Wulandhari L A,et al.Improved vertex chain code based mapping algorithm for curve length estimation[J].Journal of Computer Science,2011,7 (5):736-743.
[8]LU Rong,FAN Yong,CHEN Niannian,et al.Fast algorithm for extracting minimum enclosing rectangle of target image[J].Computer Engineering,2010,36 (21):178-180 (in Chinese).[卢蓉,范勇,陈念年,等.一种提取目标图像最小外接矩形的快速算法 [J].计算机工程,2010,36 (21):178-180.]
[9]LIU Y K,WEI W,WANG P J,et al.Compressed vertex chain codes[J].Pattern Recognition,2007,40 (11):2908-2913.
[10]CHEN P Y,CHANG C P.The segmented vertex chain code[J].Journal of the Chinese Institute of Engineers,2011,34(6):40-44.
[11]YU Goufang,WANG Li.Research on compression-type vertex chain code[J].Journal of Image and Graphics,2010,15(10):1465-1470 (in Chinese). [于国防,王莉.压缩型顶点链码的研究 [J].中国图象图形学 报,2010,15 (10):1465-1470.]

