基于曲线拟合的SINS/GPS紧密组合导航系统

肖业伟，唐辛冰

（湘潭大学 信息工程学院，湖南 湘潭 411105）

惯性导航系统具有自主性和实时性好，导航参数全等优点，但导航定位误差随时间增长，难以长期独立工作；GPS导航定位具有高精度，但其抗干扰能力差，信号受可见星的限制。SINS/GPS组合导航，克服了各自缺点，优势互补，成为当前各类飞机普遍采用的主要导航设备[1]。根据惯性导航系统和GPS系统的组合深度，可分为松散组合、紧密组合两类。松散组合通常指位置、速度组合，即将惯导与GPS接收机输出的位置、速度之差作为量测值，经过卡尔曼滤波，对惯导系统的误差进行估计和校正。而紧密组合的基本模式是伪距、伪距率组合，以及在伪距、伪距率组合基础上用惯导位置和速度对GPS接收机跟踪环路进行辅助。

SINS/GPS紧密组合导航在进行信息融合时，GPS钟差会造成量测信息值的突变，这种突变如不处理会造成滤波器的发散，且量测数据的时间同步问题也是该系统需要解决的关键问题之一。基于以上分析可知，组合导航卡尔曼滤波器的量测信息都存在一定的滞后延迟，特别是在高动态环境下导航系统的输出滞后将给量测值带来很大的误差，若直接采用这样的量测数据进行卡尔曼滤波计算必然给导航结果带来很大的误差。文献[2]对紧密组合的SINS/GPS复合导航系统在高速、高机动弹道导弹上的可行性进行了分析研究，实现了基于伪1距、伪距率的SINS/GPS紧密组合导航系统的仿真，但未考虑GPS接收机的时间同步问题。文献[3]提出了一种利用GPS接收机中1PPS（Pulse Per Second）信号作为同步标签的时间同步方法，将IMU中的数据加上精确的时间标签，从而达到时间同步的目的，但是在松散组合的前提下进行的滤波。对于量测滞后问题，文献[4-5]提出将滞后量测值与其对应过去时刻的惯导输出值进行组合导航卡尔曼滤波，然后再根据惯导其他时刻的输出值将滤波结果递推到当前时刻。然而，这种方法导致在一次滤波计算中需要进行一次量测更新和多次时间更新，因此算法比较复杂，而且精度也不高，很难适应高动态环境和高精度要求。针对此，文中提出了基于曲线拟合的SINS/GPS紧密组合导航系统，分析研究了设计该系统时遇到的问题，进而通过曲线拟合的方法来解决导航系统量测滞后的问题，最后对改进后的系统进行了仿真验证，结果达到了所要求的精度，验证了该方法的有效性。

1 SINS/GPS紧密组合导航的原理

紧密组合是组合程度较深的组合方式，其主要特点是GPS接收机和惯导系统相互辅助。为了更好地实现相互辅助的作用，通常是把GPS和惯导系统按组合的要求进行一体化设计。紧密组合的基本模式是伪距、伪距率的组合，以及在伪距、伪距率组合基础上再加上用惯导位置和速度对GPS接收机跟踪环进行辅助，也可以再增加对GPS接收机导航功能的辅助。用在高动态飞行器上的GPS／惯性组合系统通常都是采用紧密组合模式。

伪距、伪距率组合原理：惯导系统输出的位置和速度信息结合GPS给出的星历数据，可以求出相应的伪距、伪距率。将计算得到的伪距、伪距率与GPS测量得到伪距、伪距率的之差作为量测值，通过卡尔曼滤波器估计惯导系统和GPS的误差量，然后对两个系统进行反馈校正。

与位置、速度组合相比，基于伪距、伪距率的组合导航系统具有如下优点：1）直接采用了的原始观测量伪距、伪距率，无量测相关问题，并考虑了GPS接收机误差模型，可以获得更高的组合精度[6]。2）当GPS有效星数小于4时，仍可提供优于纯惯性的导航精度，具有一定的可靠性和容错性；当有效星数大于4时，通过数据冗余可以进一步提高精度。3）惯性导航系统具有较高的短期位置精度和速度精度，利用这些信息辅助GPS的接收和跟踪过程，可以提高GPS的定位精度、动态性能和抗干扰能力。

2 卡尔曼滤波器的设计

2.1 状态方程

卡尔曼滤波器的设计是SINS/GPS紧密组合导航的关键，卡尔曼滤波器的状态模型主要依据系统的误差模型，包含惯导误差模型和接收机误差模型，由于为解决钟差突跳问题采用了量测双差方式，去掉了接收机钟差对量测值的影响。故状态方程中不包含接收机钟差项，仅含惯导误差模型，SINS误差模型参考文[7]，包括速度误差、姿态和航向误差、位置误差、陀螺漂移和加速度计零偏15个状态变量：

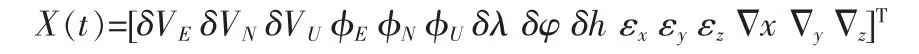
根据状态变量X（t）和系统误差模型可以得到伪距、伪距率组合的状态方程：

式中

2.2 伪距量测值构成

量测模型采用伪距组合方式。已知惯导系统解算的地理位置信息λ、φ、h，可求得地球坐标系下的位置：

根据星历给出的GPS卫星轨道信息，可确定卫星在地球坐标系中的瞬时位置xsi、ysi、zsi，从而计算出惯导位置相对于卫星i的伪距：

由此可得到相对卫星i的伪距差值

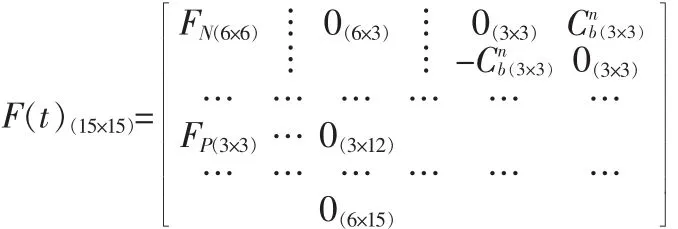
上式中δρi可直接作为量测值进行滤波计算。由于GPS接收机时钟误差引起的等效距离每秒递增，当GPS接收机长时间工作后，时钟误差累积到一定值，此时接收机将时钟误差清零，组合导航系统接收到的GPS测量伪距ρ0发生很大的跳变，进而产生了奇异值。该奇异值引起卡尔曼滤波器错误修正，导致滤波发散。

为解决这种现象，改用伪距量测差分方法。即从可见星中选择仰角最大的卫星m作为基准星，惯导相对该卫星m的伪距差值δρm=ρIm-ρGm为基准值，进一步构成量测值为：

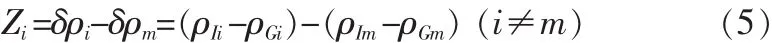
综上所述，单个伪距量测值的量测方程为：

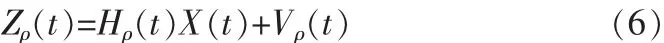
式中 Hρ（t）（1×15）=[0（1×6）…Hρ（1×3）…0（1×6）]

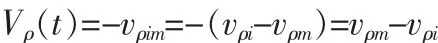
考虑噪声 vρi和 vρm不相关，则由量测噪声 Vρ（t）值的构成可知

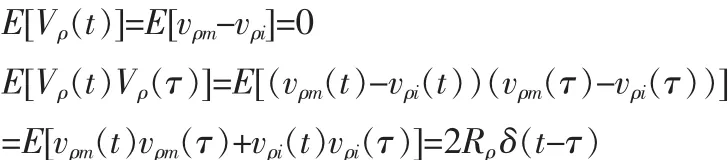
2.3 基于曲线拟合的量测预测算法

在高动态环境下，由于载体运动参数的变化十分复杂，所以不可能用某一确定的函数来精确描述载体运动参数，但是在很短的时间段内可以用简单曲线来分段拟合近似描述之。而每段的拟合曲线可以用导航系统输出的当前时刻、之前时刻的量测值以及量测更新周期T和延迟时间Δt来表示，一旦拟合曲线确定，就可以计算求得tk+Δt时刻导航系统的量测预测值 Zk+Δt。

假设在某个时刻tk+Δt获得导航系统输出的量测值Zk，该量测值带有延迟量Δt，其所对应的时刻是tk，意即Zk并不是tk+Δt时刻的量测值，而是tk时刻的量测值。并设导航系统在tk-1时刻的量测值为Zk-1，在tk-2时刻的量测值为Zk-2，其量测更新周期为T。为了便于说明，此处不妨采用抛物线来拟合预测导航系统的量测值。

在[tk-2，tk]时间段内，对导航系统输出的量测值 Z（t）作以下拟合：

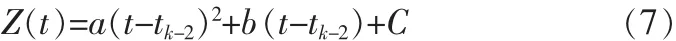
于是，每个量测更新时刻点所对应的量测值之间的时序关系如图1所示。

图1 量测更新时刻点所对应量测值之间的时序关系Fig.1 Timing relationship of measurement updates and measure value

对于 tk-2、tk-1、tk时刻，它们所对应的量测值 Z（t）分别为 Zk-2、Zk-1、Zk，即

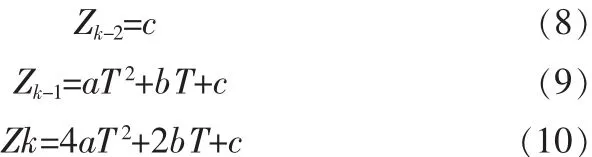
联立式（8）、（9）和（10），可以求得

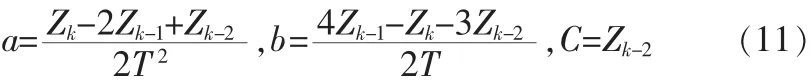
于是，根据式（7）和（11）可计算出 tk+Δt时刻导航系统的量测预测值 Zk+Δt为

从而，根据导航系统输出的当前时刻量测Zk、前两个时刻量测Zk-1和Zk-2、量测更新周期T和延迟时间Δt，就可以递推计算求得tk+Δt时刻导航系统的量测预测值Zk+Δt。然后，利用该量测预测值与tk+Δt时刻惯导系统的输出参数进行组合导航卡尔曼滤波计算，从而获得当前时刻系统误差状态的最优估计值。

上述基于曲线拟合的量测预测算法采用的是抛物线来拟合预测导航系统的量测值，根据不同的载体飞行动态和精度要求，还可以选取其他曲线来拟合预测导航系统的量测值，如直线、三次抛物线等，抛物线的阶次越高，拟合的精度越高，但计算量也越大。

3 仿真验证

为了验证前面所提出的基于曲线拟合的量测预测算法，以SINS/GPS组合导航系统为对象，分别对直接采用滞后量测的组合导航和采用量测预测的组合导航进行了仿真研究。

其中，GPS输出更新周期为1 s，输出延迟时间为100 ms。卡尔曼滤波周期为1s，仿真时间仍为1 500 s。基于上述仿真条件，首先对直接采用滞后量测的SINS/GPS组合导航进行计算机仿真，仿真结果如图2、图3所示。

根据图2～3可以看出，在完全相同的导航系统精度条件下，GPS量测输出滞后严重影响了SINS/GPS组合导航的结果：在直接采用滞后量测进行组合导航时，载体东向速度误差最大达到1.32 m/s，北向速度误差最大达到1.58 m/s，天向速度误差最大达到3.92 m/s；而纬度误差最大达到93 m，经度误差最大达到115 m，高度误差最大达到118 m。显然，量测滞后时的SINS/GPS组合导航精度很不理想，说明GPS量测输出滞后给组合导航结果带来了很大的误差。

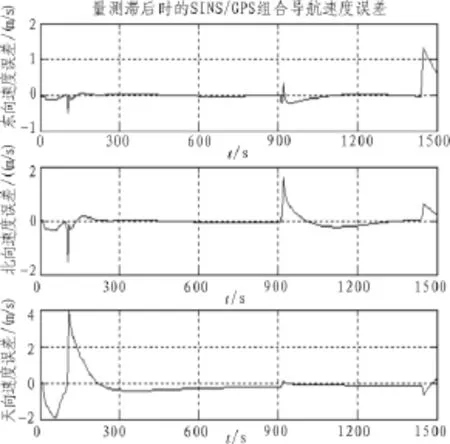
图2 量测滞后时的SINS/GPS组合导航速度误差Fig.2 Velocity error of SINS/GPS integrated navigation system based on measurement delay

图3 量测滞后时的SINS/GPS组合导航位置误差Fig.3 Position error of SINS/GPS integrated navigation system based on measurement delay

接着，在与上面相同的仿真条件下，采用文中提出的基于曲线拟合的量测预测算法对SINS/GPS组合导航进行计算机仿真，仿真结果如图4、图5所示。

根据图4～5可以看出，在相同的仿真条件下，采用量测预测后的SINS/GPS组合导航获得了较为满意的结果：经过1 500 s的仿真时间，东向、北向、天向速度误差最终稳定在0.05 m/s以内；纬度误差控制在8 m以内，经度误差控制在6 m以内，高度误差则控制在8.5 m以内。

4 结 论

本文针对工程实践中SINS/GPS紧密组合导航系统在进行信息融合时，因为接收机输出的导航信息的延时，直接影响导航系统滤波效果的问题，提出了基于曲线拟合的SINS/GPS紧密组合导航系统解决这一问题。通过采用本文所提出的基于曲线拟合的量测预测算法能够有效地解决导航系统量测滞后的问题，而且该算法计算相对简单、独立，只利用到导航系统当前时刻和之前两个时刻的量测信息，不仅计算量小，还能够较好地适应高动态环境和高精度要求，特别适用于解决诸如GPS和北斗这种量测更新频率高、量测滞后时间短的导航系统的量测滞后问题。

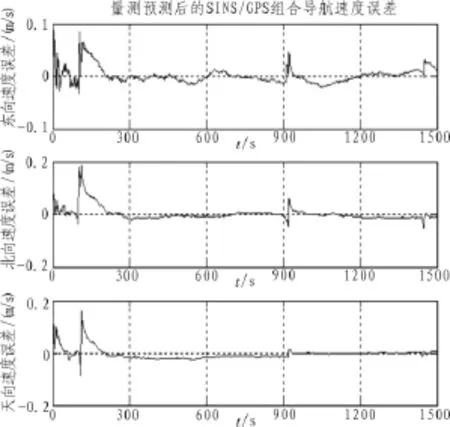
图4 量测预测后的SINS/GPS组合导航速度误差Fig.4 Velocity error of SINS/GPS integrated navigation system after measurement forecast

[1]秦永远，张洪，王淑华.卡尔曼滤波与组合导航原理[M].西安：西北工业大学出版社，1998.

[2]于洁，王新龙.SINS/GPS紧密组合导航系统仿真研究[J].航空兵器，2008（6）：8-13.

YU Jie，WANG Xin-long.Simulation of SINS/GPS tightly coupled integrated navigation system[J].Aero Weaponry，2008（6）：8-13.

[3]李倩，占星群，王立端，等.GPS/INS组合导航系统时间同步系统设计[J].传感技术学报，2009，22（12）：1752-1756.

LI Qian，ZHAN Xing-qun，WANG Li-rui，et al.Time synchronizer design in integrated GPS/INS system[J].Chinese Journal of Sensors and Actuators，2009，22（12）：1752-1756.

[4]刘建业，熊智，段方.考虑量测滞后的INS/SAR组合导航非等间隔滤波算法研究 [J].宇航学报，2004，25（6）:626-631.

LIU Jian-ye，XIONG Zhi，DUAN Fang.Processing the measurementdelay INS/SAR integrated navigation incoordinate interval filtering algorithm study[J].Journal of Astronautics，2004，25（6）:626-631.

[5]Lee Hyung Keun，Lee Jang Gyu，Jee Gyu-In.Effect of GPS measurement delay on SDINS[C]//In:IEEE Position Location and Navigation Symposium， San Diego， CA，2000：464-471.

[6]QI Hong-hui，Moore J B.Direct kalman filtering approach for GPS/INS integration[J].IEEE Trans on AES，2002，38（2）:687-693.

[7]袁信，俞济祥，陈哲.导航系统[M].北京：航空工业出版社，1993.