基于DSP的实数序列FFT算法探讨

郭建涛，范春凤

(信阳师范学院物理电子工程学院，河南信阳 464000）

“数字信号处理”是电气信息类学生的一门专业基础课程，该课程以算法为核心，其特点是理论性强，抽象概念多，对数学基础要求高，传统的以教师“单纯授课”、学生死记公式的教育模式不仅教学效果差，而且使得学生学习兴趣下降，以致今后不愿从事该领域的工作。而“DSP技术及应用”课程重点偏重数字信号处理的实现，学生尽管有浓厚的兴趣，但是由于前期的理论基础有所欠缺，学习“DSP技术及应用”课程时比较吃力，在理论深度、算法设计思想上不能融会贯通，难以达到培养创新能力、实践能力的根本要求。

傅里叶变换是一种将信号从时域转变为频域表示的变换手段，它在信号的频谱成分分析中起着基础性的作用。由于快速傅里叶变换（FFT）算法的出现，使得傅里叶变换在信号分析和系统设计中得到了广泛的应用。DSP技术由于其快速处理大数据量的能力在现代语音、图像以及视频应用中得到了快速发展，基于DSP芯片实现FFT算法显得日益重要。

本文从基本FFT算法理论出发，基于实际应用中信号多为实数数据，给出了实数序列的FFT快速算法，并结合当前通用的TITMS320C54系列DSP芯片，汇编编程实现FFT算法。经过理论分析和实验仿真，更加有助于加强对FFT算法内容的掌握和理解，大大提高了数字信号处理技术的教学效果。

1 FFT算法基本原理

1.1 N点复数序列的FFT

给定N点复数序列d（n），0≤n≤N-1。为计算方便起见，这里设N=2M，M为正整数。

d（n）的DFT为[1-2]：

将d（n）按照n的奇偶分为两组，即按n=2r及n=2r+1分为两组：

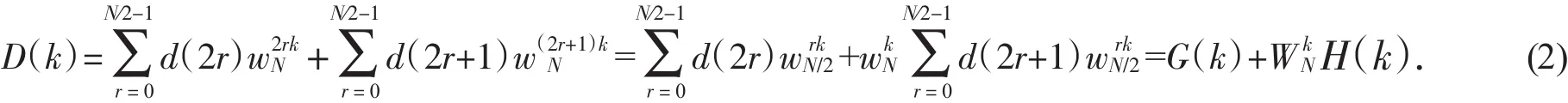
1.2 2N点实数序列的FFT

对于2N 点实数序列 a（n），n=0，1，…，2N-1，按照如下方式构成一N 点复数序列 d（n），n=0,1,…，N-1，a(2n)表示其实部，a(2n+1)是其虚部：

根据DFT的共轭对称性，知道d（n）的实部的DFT对应于D（k）的共轭偶对称分量，d（n）的虚部的DFT对应于D（k）的共轭奇对称分量：

从而得到a（n）的DFT为：

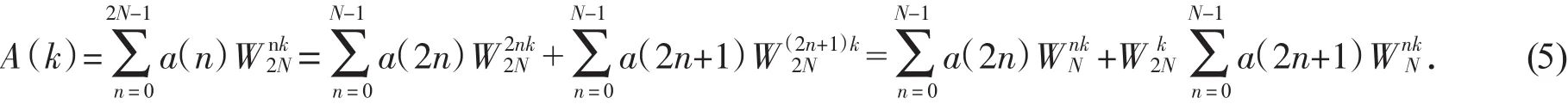
将式（4）代入式（5），得到

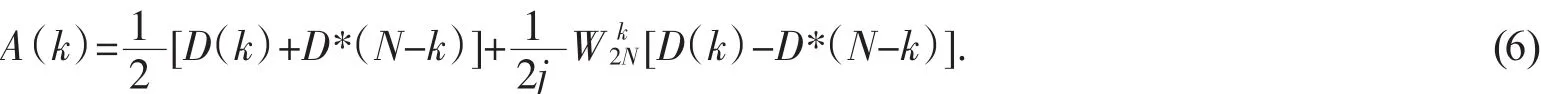
从而，一个2N点的实数序列的傅里叶变换可以通过一个N点复数序列的FFT获取。

2 FFT的DSP程序实现

下面以2N=256点的实数序列为例说明FFT的DSP实现过程。

2.1 实数FFT运算序列的存储分配

程序代码安排在0x3000h开始的存储器中，其中0x3000h～0x3080h存放中断向量表，FFT程序使用的正弦表和余弦表数据(.data段)安排在0xc00h开始的地方，长度为0x1400h（分别有256个值），变量(.bss段定义)存放在0x80h开始的地址中。设置256点实数FFT程序的数据缓冲区位于0x2300h～0x23ffh,FFT变换后功率谱的计算结果存放在0x2200h～0x22ffh中[3-4]。

2.2 基2实数FFT运算的算法

该算法主要分为以下2个步骤进行。

第一，输入数据的组合和位排序。首先，原始输入的2N=256个点的实数序列复制放到0x2300h开始的相邻单元，当成N=128点的复数序列d[n]，其中奇数地址是d[n]实部，偶数地址是d[n]的虚部。然后，依据图1输入数据的排列，把复数序列位倒序后，存储在以0x2200h开始的数据处理缓冲区中。

程序设计中，使用位倒序寻址方式可以大大提高程序执行的速度和使用存储器的效率。在这种寻址方式中，AR0存放的整数是实数数据点数的一半（此处仅仅完成位倒序），即128。输入缓冲指针AR3进行加1减1、位倒序缓冲指针AR2连续加2次，完成一个复数数据倒序。然后按照位倒序寻址方式修改AR3，即，指令：MAR AR3+0B，就可以得到下一数据地址。重复上述过程128次，即可完成输入数据位的排序工作；这一点通过设置块重复计数器BRC由RPTB块重复指令完成[5]。

第二，N点复数FFT运算。在数据处理器里进行N点复数FFT运算。由于在FFT运算中要用到旋转因子WN，它是一个复数。我们把它分为正弦和余弦部分，用Q15格式将它们存储在两个分离的表中。FFT变换关键运算主要包括蝶形结个数和单个蝶形结计算两个部分。

(1)级、组和蝶形结的个数变量及其调整

N点复数序列FFT运算的分成M级，每一级分别进行2，22，…，2M点的FFT运算，此时每一级的组数分别为2M-1，2M-2，…，1，每一级各组中的蝶形结的数目相同，不同级的蝶形结数目分布为20，21，…，2M-1（FFT运算点数的一半）。因此，算法首先制定级、组和蝶形结三个计数器，通过三层循环分别完成各级、各组合单个蝶形结的运算。

计算时，由2个数据指针PX、QX分别指向参加蝶形运算的第一个数据和第二个数据。其中，第二个数据需要乘以旋转因子（通过指向正余弦表的指针AR4、AR5完成定位）。

(2)蝶形结运算

设定参加蝶形结运算的两个输入数据分别为P、Q，包括数据的实部和虚部，用（PR、PI）和（QR、QI）表示；输出分别 P′，Q′，旋转因子用 W 表示，相应的实部和虚部表示用其后添加R和I加以明示，见图1。

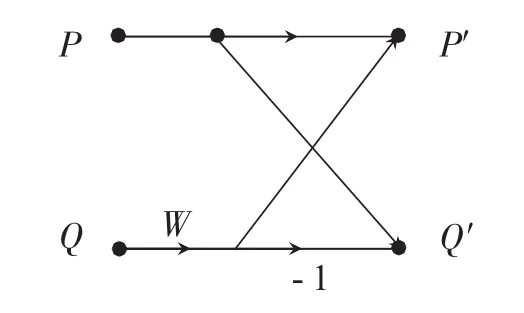
图1 单个蝶形运算

对于旋转因子W，正余弦表格给出的仅仅是正余弦值，用Q15格式将它们存储在两个分离的表中。每个表中有128项，对应0°~180°。因为采用循环寻址地址来对表寻址，128=27<28，因此每张表排队的开始地址就必须是8个LSB位为0的地址。按照系统的存储器配置，把正弦表第一项“sine_table”放在0x0C00的位置，余弦表第一项“cos-table”放在0x0D00的位置。

在计算蝶形输出时相应的实部是用减法，虚部用加法，即

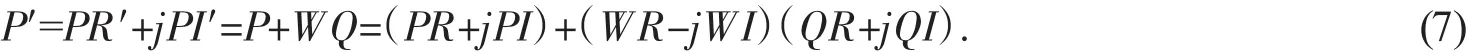
因此，蝶形结第一个输出数据的实部表示为PR′＝PR＋QR×WR+QI×WI，第一个输出数据的虚部表示为PI′=PI+QI×WR-QR×WI。同样可得到蝶形结第二个输出数据的表示形式，这里不再给出[6]。相应的关键汇编指令如下：

其中，第二个数据与系数相乘后，所得结果是32位数，与第一个数据的实部相加时，需要将该实部数据左移16位后执行；并行指令可以在一个指令周期内，将B高端移位ASM，存于AR2所指定的存储单元中，并执行将AR2所指的单元中的值左移16位后减去累加器B的值；在实际编程时，为了避免溢出，对每一步的输出右移一位（相当于将结果除以2，相当于把的比例因子分散到各级运算之中，可以在保持输出信号方差不变、输出信号最大幅度等于输入值N倍的情况下，减小输出噪声电平，增加输入信号幅度）。应该指出，在FFT的各级运算过程中，相应的中间结果、FFT输出和整理后的结果都存储在该缓冲区中，从而实现原位计算。

第三，产生输出结果。这里将D（k）重新表示为实部和虚部的形式[7]：

代入式(6)可以得到2N点实数序列的DFT表示式：

A（k）=AR（k）+jAI（k）

从而有

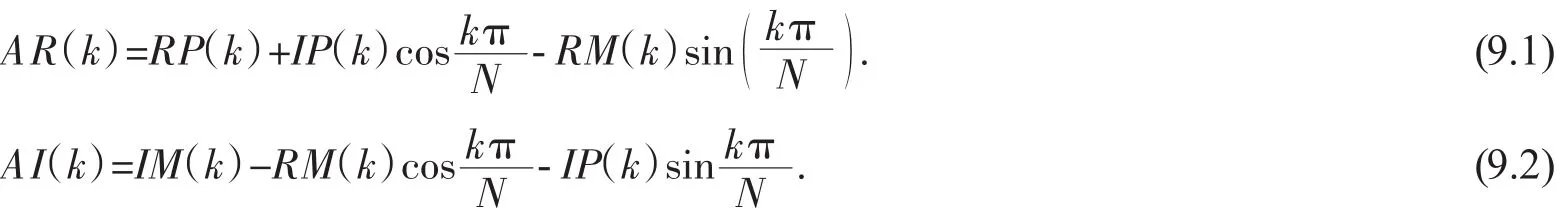
其中，RP（k）和 IP（k）分别表示 D（k）的偶对称部分的实部和虚部，RM（k）和 IM（k）分别表示 D（k）的奇对称部分的实部和虚部，即

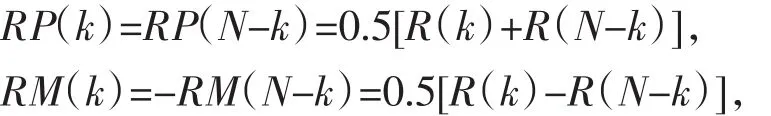
编程时首先实现输出复数序列的奇偶分解，求解RP(k)、IP(k)、RM(k)和IM(k)。这一点通过4个指针分别指向R(k)、R(N-k)、I(k)和I(N-k)，然后完成式(10)的计算。程序最后按照原始序列的DFT对上述结果按照式(9)计算，并以自然顺序存储在整个4N长的数据缓冲区内。

3 实验结果与分析

给定包含两个频率分别为5Hz、10Hz正弦信号，采样频率200Hz，取数据长度为256。将Matlab生成的信号源文件转换为CCS能够识别的.dat格式，这里命名为input.dat文件。在CCS中，首先设置探针断点Toggle Probe point，从File菜单项中选择File I/O，在出现的窗口中选择输入文件input.dat。单击Add Probe Point，出现探针断点窗口下，将输入文件与设置的探测点连接起来。根据公式(3)将a(n)组合为复数序列d(n)，经过128点的FFT后得到其傅里叶变换D(k)，并顺序存放在0x2200h-0x23ffh的缓冲区中，前半部分为d(n)、后半部分为D(k)，如图2。由于复数的实部和虚部分开存放，因此一共占用512个字长。图3是256点实数序列a(n)的傅里叶变换A(k)，频谱关于零频对称，相应的功率谱显示在图4中，与A(k)不同的是，功率谱仅有256点。为了比较起见，图5给出了利用Matlab软件计算得到的实数序列a(n)的功率谱结果，与图4相比较，可知DSP算法汇编程序给出了信号正确的傅里叶变换结果。

图2 D(k)和输入信号

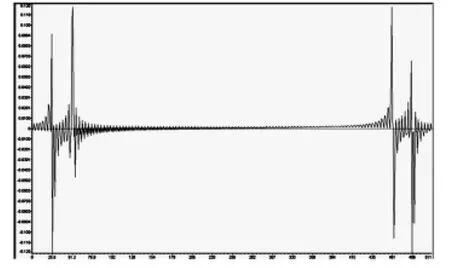
图3 实数序列的FFT

图4 信号功率谱（ccs）

图5 信号功率谱（Matlab）

4 结论

2N点实数序列可以用N点FFT算法实现，实验证明，在TMS320VC5416定点DSP中运行结果正确。同样该程序经过简单的参数修改可以适用于其它点数的信号傅里叶变换，并应用于实际系统中。这种从理论到实现的流程教学方法，不仅增强了实际的教学效果，也有助于培养学生的工程实践和创新能力。

[1]吴镇扬.数字信号处理[M].北京:高等教育出版社,2004.

[2]陈佩青.数字信号处理教程[M].北京:清华大学出版社,2007.

[3]赵宏怡.DSP技术与应用实例[M].北京:电子工业出版社,2008.

[4]陈金鹰.DSP技术及应用[M].北京:机械工业出版社,2011.

[5]刘和平.TMS320C240xDSP C语言开发应用[M].北京:北京航空航天大学出版社,2003.

[6]邱立存,闻武,刘海英.TMS320C54X系列DSP上FFT运算的实现[J].微计算机信息,2005(7):136-137.

[7]肖宛昂.嵌入式系统中FFT算法研究[J].单片机与嵌入式系统应用,2003(4):68-69.