铁路客运站旅客聚集分布仿真模型与算法研究

王爱丽,董宝田,高春霞

(北京交通大学交通运输学院,北京100044)

铁路客运站旅客聚集分布仿真模型与算法研究

王爱丽,董宝田*,高春霞

(北京交通大学交通运输学院,北京100044)

将计算机仿真技术应用于铁路客运站客流到站分布和聚集人数获取与处理,为枢纽设施的合理布局和运营管理方案编制提供依据.对北京南站进行实地调查,分析旅客在候车室的到达规律,采用拟合工具提出旅客提前到站时间分布密度函数,建立旅客到达规律模型;基于旅客到达规律模型,提出旅客到达仿真算法,仿真旅客到站乘车的过程;设计车站客流变化仿真系统,提出仿真计算车站聚集人数的方法;根据北京南站客流时空分布特征,基于列车时刻表,模拟车站客流变化,以观察枢纽旅客到站聚集波动情况,验证本文所提模型的合理性和有效性.

铁路运输;聚集人数;客流到达分布;计算机仿真;北京南站

1 引 言

枢纽设施的合理布局、设计和运营管理方案编制,需要了解车站旅客聚集分布情况[1],这样才能制定合理的措施,完成车站运营管理以及其他相关工作.客流到站聚集[2-4]分布主要由客流随时间到达规律、客流空间分布规律、列车时刻表和交通分担率等因素决定.客流的聚集情况具有概率分布特征,为了清晰、直观地反映枢纽内客流聚集波动状况,可采用计算机仿真的方法,建立客流动态仿真系统[5],模拟不同客流在复杂车站环境中的集散效率和车站设施利用等方面实用可靠的结果,从而为合理安排车站设施,科学制定客流组织方案和应急疏散方案提供可靠的技术手段和决策支持.

车站客流到站分布和旅客最高聚集人数是研究铁路客运站设施利用率、服务水平、站舍能力与规模的核心[6].根据目前计算机的广泛应用的现状及将来铁路客运站设计的需要,本文将计算机仿真技术应用于铁路客运站客流到达分布和聚集人数获取与处理.分析了旅客在候车室的到达规律,采用拟合工具提出旅客到达规律分布函数,结合列车时刻表仿真旅客到达车站的时间过程;并设计开发了客流仿真系统,仿真旅客到站聚集过程,统计每一时刻旅客在各区域的聚集量,计算车站的最高聚集人数.研究结果表明,系统是对实际情况模拟,它的应用能够提高效率,结果精确,并能够记录最高聚集人数产生的时间,对车站客流组织工作更加有利.

2 铁路客运站旅客聚集规律模型与算法的建立

2.1 旅客到达规律模型建立

本文通过对北京南站的旅客提前到达车站的时间进行统计,对数据进行频数统计和归一化处理后,运用拟合优度检验方法[7],采用matlab对旅客提前到站时间进行曲线拟合,发现旅客提前到达时间分布大致服从复合负指数分布[8].

复合负指数分布函数形式如下:

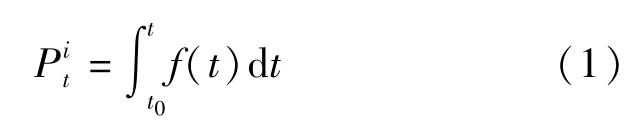
式中 Pit——在计算时刻t时准备乘坐第i列车并已经到达车站的旅客占列车定员的比例,单位为%;

t——计算时间,单位为min;

i——列车序号;

t0——乘坐第i列车的旅客第一个进入候车室的计算时间,本文取t0=0(min);

f(t)——旅客到达分布密度函数,分布形式为

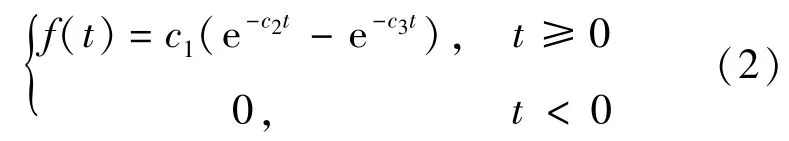
考虑所有旅客应该在列车出发前全部到达候车室,故有:

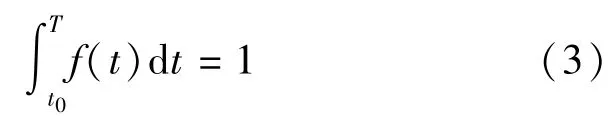
式中 T——乘坐第i列车的乘客最后一个进入候车室的计算时刻,单位为min.对于T的取值各文献有所不同,根据调查结果,本文建议T=100min,即行人提前到达时间t在区间[0,100]内产生行人的概率接近100%.建议在实际计算时可根据车站所在城市的具体情况对T值进行灵活确定.

项目组对北京南站做了一些问卷调查和实地调查,根据所得数据对参数c1,c2和c3的取值进行研究.该次调研活动共取得旅客数据1 268条,其中有效数据为 1 194条,主要来自于 C2021、C2049、C2051、C2277、D31、D35、D385等11个车次的旅客候车时间信息.根据实地调查结果绘制出乘客提前到达时间分布图,如图1所示.

根据对北京南站旅客提前到达车站时间的调查结果进行复合负指数分布拟合,经过多次计算,在 T=100 min时最终选取 c1=3.139 7, c2=0.020 3,c3=0.066 5,拟合的结果如图2所示,可以看出两者的拟合程度较好.当T值发生改变时,对c1,c2和c3的取值要重新考虑.需要说明的是,拟合结果存在一定的误差,为了减小误差,本文引入一个误差系数γ来调整误差.因此,在某站第i列车定员已知条件下,通过上述分布可以计算时刻t时由该类车引起的候车人数,其分布密度公式如下:

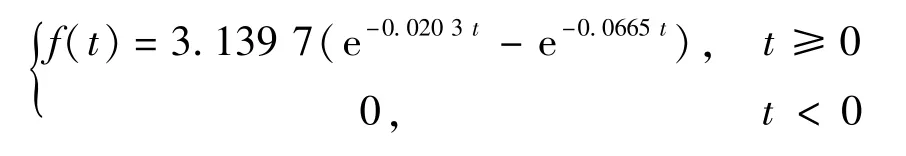
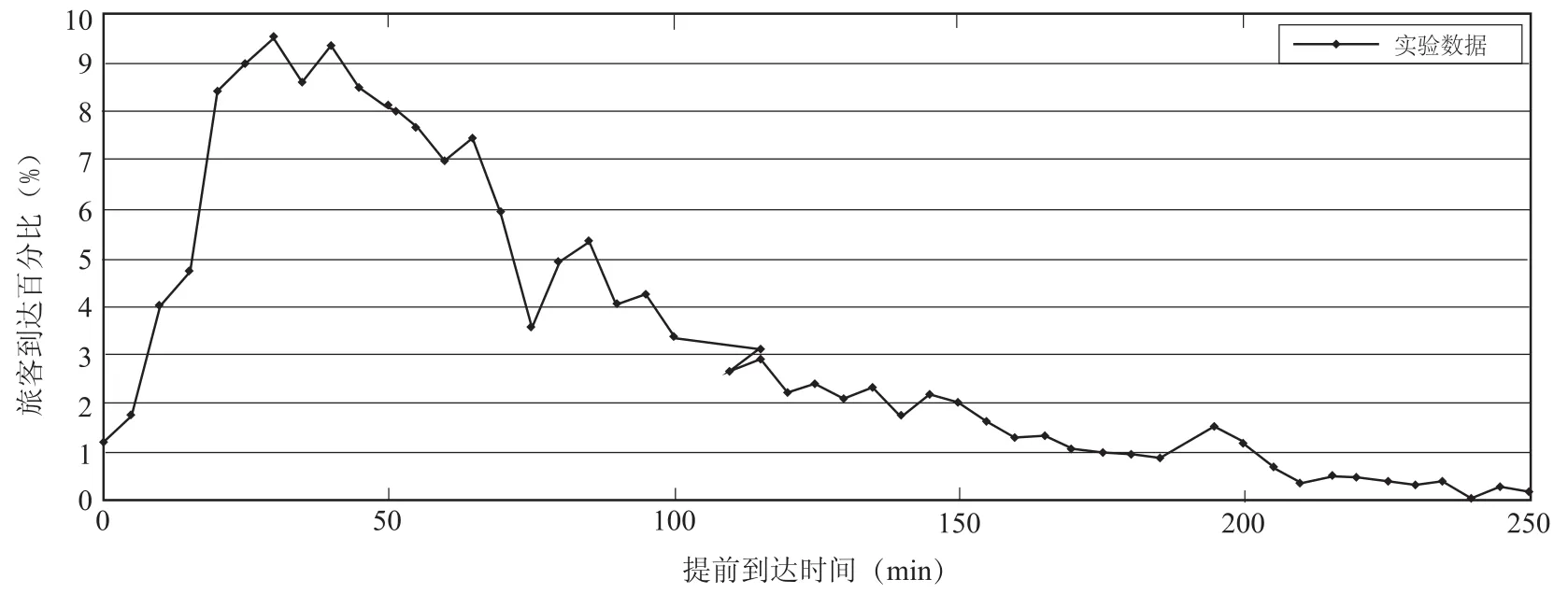
图1 北京南站旅客候车时间调研数据Fig.1 The research data of passenger waiting time at Beijing south station

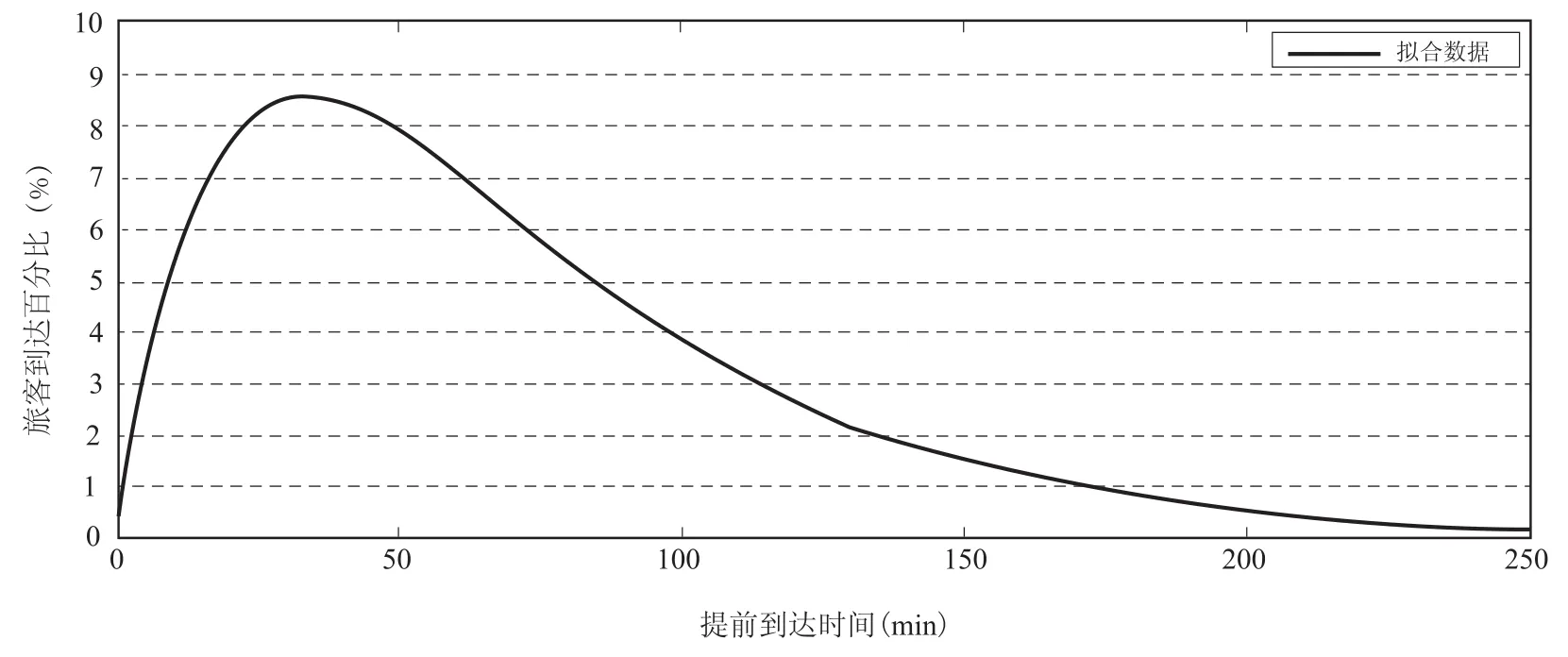
图2 复合负指数分布拟合图Fig.2 Composite negative exponential distribution fitting chart

2.2 到达车站的旅客聚集人数计算模型

根据乘客提前到达车站的时间分布数据,结合列车时刻表,计算车站各次列车到达车站的旅客人数,从而得到任意时刻(精确到分钟)到达车站的旅客聚集人数.计算模型如下:人数;

n——产生旅客的列车数.

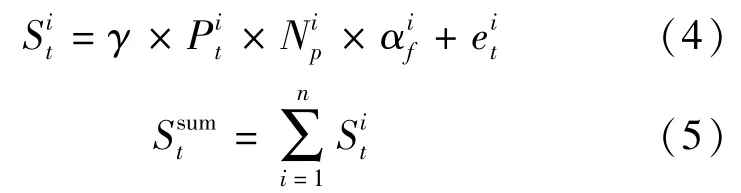
式中 Sit——计算时刻t时第i列车到达车站的乘车人数;

γ——误差系数;

Ni——第i列车在该站的定员;p

αi———第i列车满座率,一般在区间[0.7,f1.2]之间;

ei———计算时刻t时第i列车带来的送站t人员,可取列车发送旅客人数的1.5%～3%; Ssum——计算时刻t时到达车站的总聚集t

2.3 仿真旅客到达算法的建立

确定每列旅客列车的发车时间和旅客发送量,根据复合负指数分布计算在不同的提前时间到达车站的旅客数量,然后把这些数值根据相对应的列车加载到连续的时间序列中,产生旅客到站时间分布,仿真车站客流的到达过程.

假设枢纽的第一趟车的发车时间leave_time为7:30(如表1所示),那么产生行人的最早时间就是在这个时间上向前推移100 min,即仿真开始时间start_time=5:50,从5:50以后就有旅客依次到达乘车.为了降低计算复杂度,本文采用逆推法,根据复合负指数分布计算某个时间段的单列车旅客到达量.随着统计产生行人时钟T的推进,当0＜= span_time[i]-T＜=100时,乘坐列车i且其提前到达时间t在[span_time[i]-T,100]区间内的到站聚集人数people[i]和总的到站聚集人数Ssum为

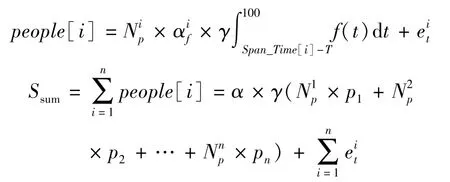
式中 span_time[i]——仿真开始时间start_time与列车i发车时间leave_time[i]之差;

T——统计产生行人时钟的推进时间,其初始值等于0,最大值不能超过span_time[N].

采用此方法计算表1中列车的到达规律分布(如图3所示),时钟T=30的到站聚集人数P1sum、 T=40的到站聚集人数P2sum和当前时间段到达的人数p[j]分别为

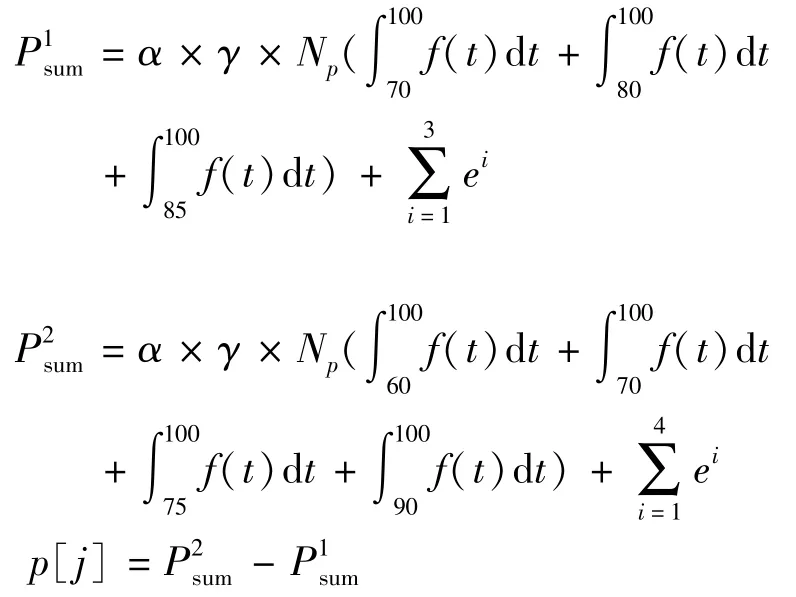
表1 列车时刻表Table 1 Train schedules

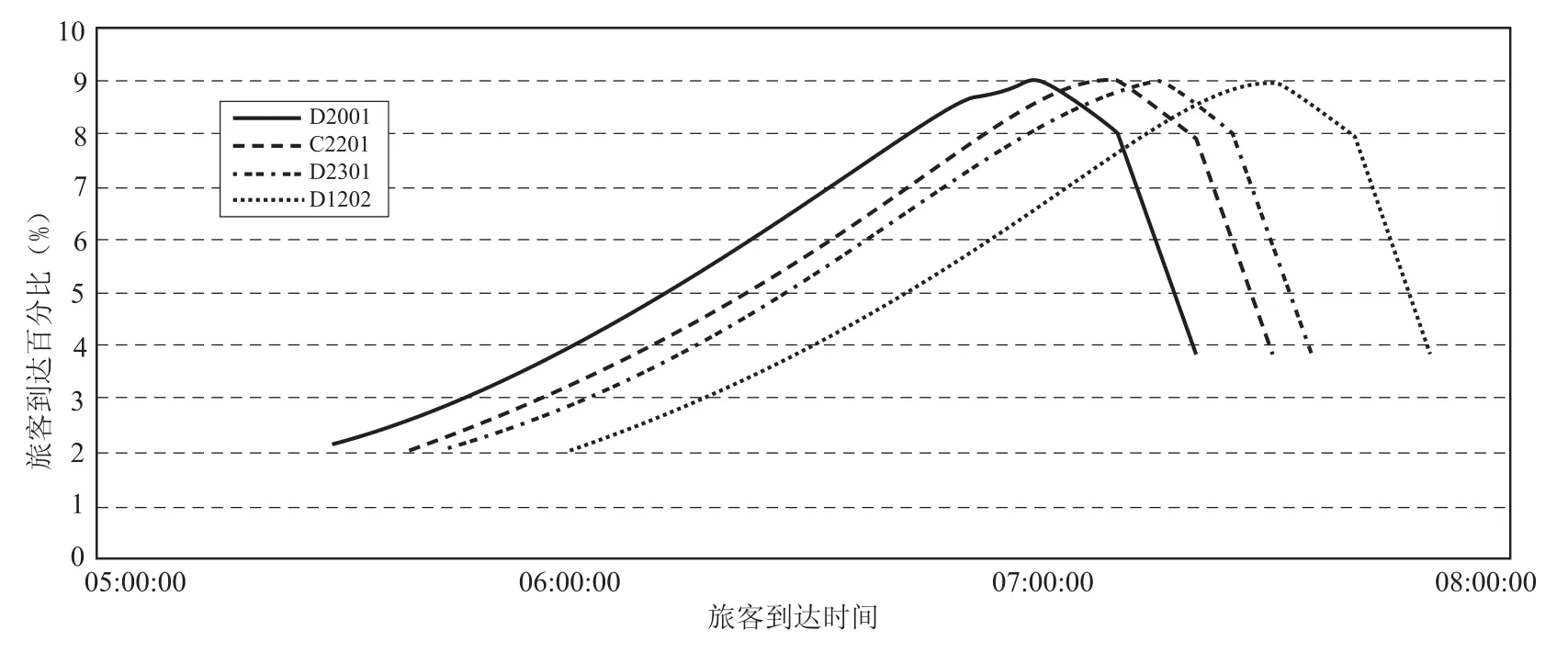
图3 多列车旅客到达时间分布曲线Fig.3 Curve of passengers'arrival time of several trains

整个算法的基本步骤如下:

步骤0初始化:读取发车列车时刻表和列车定员,根据第一趟列车的发车时间leave_time[1],算 出 产 生 乘 客 的 最 早 时 间 start_time =leave_time[1]-100,并定义仿真推进时间T= 0、推进时间间隔Interval和时间间隔次数j=1;

步骤1根据列车时刻表计算每趟车的时间间隔span_time[i],即第一个乘客到达车站候车的时间与列车 i发车时间之差:span_time[i]=leave_time[i]-start_time;

步骤2while:判断仿真推进时间T是否小于span_time[N],若小于转到步骤3,否则转到步骤5;

步骤3搜索产生乘客的列车,for:i=1;i＜= N;i++,if:乘坐列车 i且其提前到达时间span_time[i]-T在[0,100]区间内,则计算列车i产生的乘客people[i]和到站的总聚集人数Sjsum= Sj+people[i],变量 i加1,重复步骤3;else:

sumi++,重复步骤3;

步骤4仿真时钟 T推进一步:T=T+ Interval,并记录这段时间间隔内要到达的人数p[j]=Sj-Sj-1,然后变量j加1,转至步骤2;

sumsum

步骤5计算结束.

计算出每个时间间隔Interval内将要产生的人数后,将这些人数在这段时间内均匀分布,然后调用Produce()函数生成乘客.在产生乘客时,乘客的编号、质量、占用空间、期望速度、车次等属性(如表2所示)依次按一定规则产生.

表2 乘客信息表Table 2 Pedestrian information table

3 仿真系统的设计与实现

通过客流仿真系统实现旅客在枢纽内行为的动态仿真,自动统计每一时刻旅客在各区域的聚集量,计算车站的最高聚集人数.客流仿真系统利用旅客提前到达时间分布生成旅客到达量,根据到站客流的城市交通分担率,将客流分担到各种交通方式,然后进行动态仿真.

3.1 系统设计

该系统主要包括客流产生、仿真控制、客流显示和客流统计四大模块.客流产生模块用来模拟旅客到达分布数据、列车时刻表以及每列车的发送人数或列车定员和满座率等文件;仿真控制模块通过建立行人运动模型,以及客流设施服务模型,在碰撞检测及规避和路径选择的规则之下对到达枢纽的客流进行仿真;客流显示模块将枢纽内客流运动状态由动画演示形式给出;客流统计模块用来统计每一时刻旅客在各区域的聚集量、速度、密度等数据,以图形或表格的形式输出.

3.2 系统算法和流程

整个系统的基本步骤如下(如图4所示):

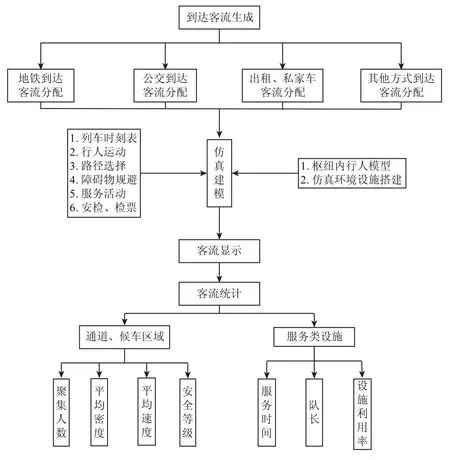
图4 系统流程图Fig.4 System flow chart

步骤1输入列车时刻表、定员Np、交通分担率和乘客属性等参数,利用复合负指数分布密度函数f(t),以Interval为客流生成间隔,生成枢纽的旅客到达时间分布;

步骤2搭建枢纽仿真环境,将乘客移动枢纽环境抽象为一平面坐标系;

步骤3依据枢纽设计方案和乘客交通行为特性进行客流组织仿真建模;

步骤4读取客流到达信息和仿真环境设施信息,通过建立乘客交通仿真模型对到达枢纽的客流进行动态仿真,得到客流在不同设施内的时空分布数据,并将数据写入数据库;

步骤5对仿真数据进行分析和处理,得到车站各个区域的聚集人数、平均密度、平均速度等数据,并将相关数据输出到用户界面,结束.

4 算例分析与讨论

在Visual Studio2008软件平台下,应用C#语言和SQL server数据库,开发了模拟客流到站分布的仿真系统.变更列车开行方案,应用该系统对北京南站高架候车层的不同客流强度进行动态仿真,观察枢纽客流到站聚集波动情况,对其聚集人数进行计算.

4.1 基础数据及仿真方案设计

(1)仿真方案1.

具体试验场景设计为:全日共发送列车98列,其中京津城际动车组74列(定员610),其它方向动车组24列(定员1 230).在21:00-22:00时段内共发送11个车次的列车,是全日发车数最大小时.旅客到达车站规律符合复合负指数分布,满载率αf=100%;京津城际动车组旅客提前15 min检票,其它方向动车组旅客提前20 min检票.交通方式承担比例:地铁50%,公交20%,出租车18%,私家车10%,其他方式2%;系统仿真初始时间为4:30,结束时间为23:00,仿真时钟取0.5s.

(2)仿真方案2.

具体试验场景设计为:全日共发送列车149列,其中京津城际动车组75列(定员610),京沪高铁46列(定员1 230),其它方向动车组28列(定员1 230);在7:30-8:30时段内共发送14个车次的列车,在10:30-11:30时段内共发送13个车次的列车,在13:30-14:30和15:30-16:30时段内共发送12个车次的列车.其它参数与仿真方案1相同.

4.2 仿真结果分析

通过仿真获得各方案全日客流聚集波动情况,从仿真结果可以看出,不同的组织方案导致车站发送能力和最高聚集人数不同.经过分析可以得到以下结论:

(1)仿真方案1结论.

全日客流聚集波动情况如图5(a)所示,从图中可以看出日客流形态呈现全峰型,全日内的客运需求总体维持在一个较为均衡的水平,全站绝大多时间内服务水平较高,高峰时间段内服务水平有所下降,分别在08:00、14:00和21:00时产生3个小高峰,在21:10全站客流聚集达到最高峰,为6 017人.全站聚集人数峰值出现的时间与列车发车高峰时段毗邻.

(2)仿真方案2结论.

最高聚集人数计算的结果和仿真过程如图5 (b)所示,从图中可以看出日客流形态同仿真方案1相同,也呈现全峰型.由于列车开行方案的变化,导致车站候车室的服务水平下降,聚集人数明显增加,全日内的客运需求总体维持在一个较为紧张的状态,分别在08:00、10:00、14:00和16:00时产生4个小高峰.在10:10时,达到全日最高聚集时段,聚集人数为10 020人.同样,全站聚集人数峰值出现的时间与列车发车高峰时段毗邻,反映了旅客聚集受列车时刻表驱动的关系.

5 研究结论

铁路客运站日客流聚集波动情况形成机理复杂,与列车开行方案、车站旅客组织等诸多因素有关.本文将计算机仿真技术应用于铁路客运站聚集人数获取与处理,为车站方案设计、运营管理方案编制提供参考.对北京南站进行了实地调查,分析了旅客在候车室的到达规律,对数据进行频数统计和归一化处理后,采用拟合工具提出旅客提前到站时间分布密度函数,建立模拟旅客到站算法;在此基础上,提出仿真计算车站聚集人数的方法,并采用北京南站数据进行校核检验,验证了本文所提模型具有一定的理论和使用价值,为配备车站设施和确定乘客疏散方案等提供数据依据.

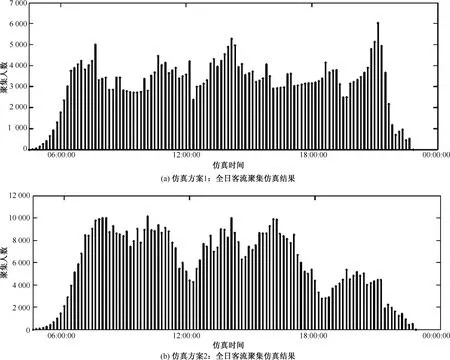
图5 不同列车开行方案客流到站聚集波动情况Fig.5 Passenger gathered fluctuations of different train operation plan

[1]张知青,吴强,徐瑞华.城市轨道交通系统故障时的客流动态分布仿真研究[J].城市轨道交通,2006, 4:52-55.[ZHANG Z Q,WU Q,XU R H.Simulation on the dynamic distribution of passenger flow in urban rail transit[J].Urban Mass Transit,2006,4:52-55.]

[2]刘启钢,朱克非,杜旭升.大型客运站最高聚集人数仿真计算方法研究[J].铁道学报,2011,33(8):1-6.[LIU Q G,ZHU K F,DU X S.Research on calculation method of the maxim um number of gathering passengers in large stations[J].Journal of Railway, 2011,33(8):1-6.]

[3]李建斌.客运专线旅客最高聚集人数计算方法初探[J].交通运输工程与信息学报,2007,5(1):9-10. [LI J B.Research on the method of calculating the maximum assembly at passenger railway line station [J].Journal of Transportation Engineering and Information,2007,5(1):9-10.]

[4]张天伟.铁路客运站旅客聚集规律研究[J].铁道学报,2009,31(1):31-34.[ZHANG T W.Research on the assembling rule of passengers at railway passenger stations[J].Journal of Railway,2009,31(1): 31-34.]

[5]何宇强,毛保华,丁勇,等.铁路客运站最高聚集人数模拟计算研究[J].系统仿真学报,2006,18(1): 213-216.[HE Y Q,MAO B H,DING Y,et al. Research on simulative calculation of maximum assembling of railway passenger station[J].Journal of System Simulation,2006,18(1):213-216.]

[6]何宇强,毛保华,陈绍宽.铁路客运站旅客最高聚集人数计算方法研究[J].铁道学报,2006,28(1):6-11.[HE Y Q,MAO B H,CHEN S K.Research on the methods of calculating the maximum assembling at railway passenger stations[J].Journal of Railway, 2006,28(1):6-11.]

[7]唐家德.基于MATLAB的非线性曲线拟合[J].计算机与现代化,2008,6:15-19.[TANG J D.Non linear curve fitting based on MATLAB[J].Computer and Modernization,2008,6:15-19.]

[8]高春霞,董宝田,李乾.北京南站客流分析[J].物流技术,2010,12(230):18-19.[GAO C X,DONG B T,LI Q.Analysis of passenger flow of Beijing south station[J].Logistics Technology,2010,12(230): 18-19.]

Assembling Model and Algorithm of Railway Passengers Distribution

WANG Ai-li,DONG Bao-tian,GAO Chun-xia
(School of Traffic and Transportation,Beijing Jiaotong University,Beijing 100044,China)

Computer simulation technology is applied to acquire and process passenger flow distribution and assembling.It also provides reference for layout of station facilities and complication of station operation and management plan.On the basis of the investigations on Beijing South Station and analysis of the rule of arrival passenger in the waiting room,the distribution density function is proposed and the passengers arrival simulation model is developed.Then,the paper presents the passenger regularity arrival algorithm for simulating the arrival waiting process of passengers.The passenger flow simulation system is designed and the assembling calculation method is presented with simulation.According to the time and space distribution characteristics of passenger flow at Beijing South Station,the simulation experiment is conducted to observe the passenger flow dynamic distribution based on the train schedules.The rationality and effectiveness of the proposed model is thus verified.

railway transportation;assembling;arrival distribution of passenger flow;computer simulation;Beijing south station

TP391.9

A

TP391.9

A

1009-6744(2013)01-0142-07

2012-09-07

2012-10-26录用日期:2012-11-06

国家863高技术研究发展计划(2009AA11Z207);北京交通大学基金资助项目(2012YJS065).

王爱丽(1987-),女,甘肃白银人,博士生.

*通讯作者:btdong@bjtu.edu.cn