突发事件应急血液调剂问题的两阶段决策方法

王恪铭,马祖军,周愉峰

(西南交通大学a.交通运输与物流学院;b.经济管理学院物流与应急管理研究所,成都610031)

突发事件应急血液调剂问题的两阶段决策方法

王恪铭a,马祖军*b,周愉峰a

(西南交通大学a.交通运输与物流学院;b.经济管理学院物流与应急管理研究所,成都610031)

基于血液的生理特性及应急保障特性,以应急血液最晚运达时间最小、接收时的最低新鲜度最大、运输总费用最小为目标,建立考虑多品种、多式联运的应急血液调剂出救点选择,即运输路线安排问题两阶段决策优化模型,并设计了一种包含局部邻域优化的遗传,即禁忌混合算法进行求解.以“5.12”汶川大地震应急血液保障为背景构建算例,分析验证了两阶段决策方法在最晚抵达时间、新鲜度均值、运输总费用、血液积压量等指标上的优越性.

物流工程;血液调剂;两阶段决策;出救点选择;运输路线安排

1 引 言

血液在突发事件伤员救治中起着至关重要的作用.由于需求量大,事发地血站的库存与采集量往往难以满足临床需求,需要从非灾区血站紧急调剂,根据实际情况可能需要进行多次调剂,并涉及多种运输方式.因此,需要解决出救血站选择与多式联运线路安排的集成优化问题.

目前已有不少学者研究了应急出救点选择问题[1-3]和应急物资多式联运问题[4-7].但应急血液保障具有区别于一般应急物资调运的显著特性:

(1)灾后初期无法准确预测用血需求量,因而往往过高估计血液需求,对灾区血站紧急补充大量血液,由此可能造成应急保障期结束后的大量血液积压、过期(如“9.11”事件后有高达30多万单位的血液过期报废[8]);

(2)血液有多种不同的血型和成分制品;血液有保质期限制(全血与红细胞制品一般只可保存35天),且随着储存时间的延长质量下降,但失血性伤员的救治需使用新鲜度较高的血液[9];

(3)运输过程会对血液的质量造成影响,随着运输时间增加,其变质过程加速[10].

因此,调剂决策时应考虑出救血站所提供血液的新鲜程度,以及运输过程对血液质量的影响.但上述文献均以应急物资的运输费用或未满足率为目标,未考虑调运时间、运输方式对所运物资质量的影响,均假设需求是确定的或服从某种已知的不确定分布.此外,出救点选择与救援物资运输路线安排之间并非相互独立,有必要对其进行集成优化管理.

鉴于血液的生理特性及应急保障特性,为提高调剂血液抵达各灾区血站的及时性、质量与效率,文中以应急血液最晚运达时间最小、各受灾血站接收血液新鲜度的最小值最大、运输总费用最小为目标,建立了考虑多品种、多式联运的应急血液调剂出救点选择—运输路线安排问题的两阶段决策优化模型.之后,设计了一种结合运输组合邻域优化方法的遗传—禁忌混合算法进行求解.最后,以“5.12”汶川大地震应急血液保障为背景构建算例进行分析.

2 问题描述

设突发事件应急血液调剂过程中,出救血站、灾区血站相互之间存在多种运输方式可以选择(如图1所示,各血站之间不同线状的弧线表示不同的运输连接方式).在应急血液需求不确定的情况下,需要做出适当的应急血液调剂决策,以合理选择出救血站,并优化多式联运路线安排,以提高调剂的及时性与效率,保证运抵血液的质量,并减少应急救援期结束后灾区血站的血液库存积压量.

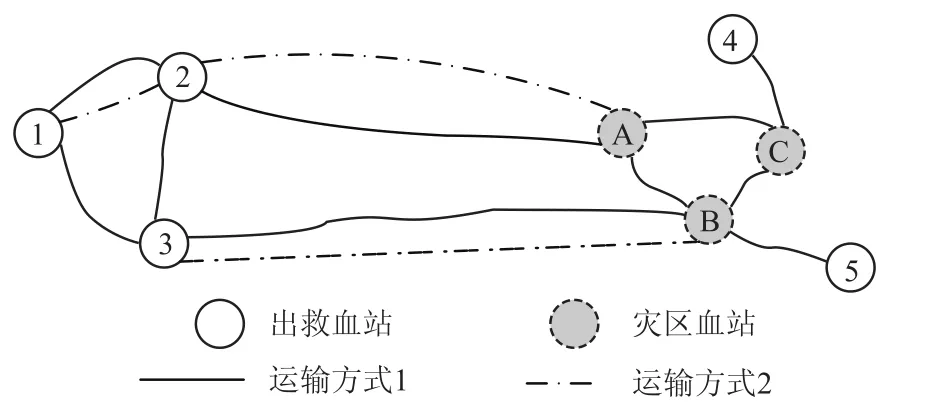
图1 血液调剂多式联运示意图Fig.1 Multi-modal transportation network for emergency blood transferring

设突发事件应急救援分为初期响应和紧急救援两个阶段进行应急血液调剂决策:在初期响应阶段,根据血液需求量的粗略预测及时进行血液调剂;在紧急救援阶段,用血需求主要来源于伤员的生理功能恢复性手术,此时需救治的伤员人数、伤情程度等与血液需求相关的信息基本明确,可较准确估计出用血需求.

建模之前,作如下假设:

(1)鉴于血液质量随着运输时间增长而下降的特性,借鉴易腐品呈指数性变质的假设[11],设s阶段血液从 g地运抵 e地之后的新鲜度为 fges= exp(-θτge)fgs.fgs(0≤fgs≤1)为s阶段g地待调剂血液的新鲜度,用该地各待调剂血制品剩余使用期与保质期之比的均值表示;θ(θ＞0)为变质率; τge为g地至e地的运输时间.

(2)在第二阶段中,血液调剂来源可以是原出救血站,也可以是某类血液制品有多余库存的灾区血站.

(3)考虑空运和汽运这两种应急血液保障中常用的运输方式,灾区血站之间采用汽运,并设血液调剂过程中运力都能满足运输要求.

3 应急血液调剂两阶段决策优化模型

3.1 符号说明

(1)参数.

T——应急救援期划分成周期的集合,T={t| t=1,2,…,tend};

S——应急血液调剂决策阶段的集合S={s|s =1,2};

ts——第s阶段的开始周期,ts∈T;

O——初始候选出救血站的集合,o∈O;

E——灾区血站的集合,e,h∈E;

N——所有血站的集合,N=O∪ E,i, j,g∈N;

M——运输方式的集合,且M={m|m=pl, ca},其中pl、ca分别表示空运和汽运;

P——血制品种类的集合,且P={p|p=wb, bp,rc},其中wb、bp、rc分别表示全血、血浆、红细胞悬液;

K——血型的集合,K={k|k=A,B,O,AB};

γk——k血型血液所占比例;

λp——p类血制品所占比例;

TUs——s阶段血制品运抵灾区的时间限制;

τm——i地至 j地运输方式 m所需的运输

ij时间;

capm——运输方式m的装载容量;

C——每单位制品运输中转所需的费用;

Cm——在i-j区间采用运输方式m的运输

ij费用;

ep(t)=λpγke(t),e(t)为e地t周期各类血液制品的预测需求总量;

dkp——e地s阶段k血型p制品的实际用量,

es

3.2 模型建立有dkesp=λpγkDes,Des为e地s阶段的血液总用量.

(2)中间变量.

τge——g地供应的血制品运抵e地总共所需时间,包括启动准备时间、运输时间及中转时间.例如,若只在 j地中转,则 τge=max(τdm+ τmgj+τ,τdm′)+τm′je,其中,τ为运输中转所需的固定时间,τdm、τdm′为运输方式m、m′的启动准备时间;

fres——e地s阶段接收血液的新鲜度;

Ikp——e地s阶段结束时k血型p制品的库

es存量;

Bkesp——e地s阶段k血型p制品需要调剂的数量;

BUkgps——g地s阶段k血型p制品的供应量.

(3)决策变量.

bkgpeijs——s阶段由血站g调剂往灾区血站e并经过i→j区间的k血型p制品的运输数量;

qkispmm′——s阶段在i地由运输方式m转换成m′的k血型p制品的数量;

vhmijs——s阶段i-j区间所需运输方式为m的运输工具数量;

xgs——0-1变量,s阶段g地血站被选择为出救血站时为1,否则为0;

xm——0-1变量,s阶段i-j区间选择运输方

ijs式m时为1,否则为0.

式(1)是使s阶段参与出救的血站所供血液运抵灾区所需最长时间最小化;式(2)是最大化s阶段灾区血站接收血液的最低新鲜度;式(3)是最小化s阶段的运输费用.式(4)为s阶段血站的供应能力约束;式(5)为s阶段的血液调剂量约束;式(6)为i地的血液运入量与运出量平衡约束,i地运输方式m的运出量由在i地运输方式m′转换为m的运量、i地出救的且运输方式为m的运量、途经i地运输方式仍为m的运量三部分组成;式(7)为s阶段i-j区间采用运输方式m时所需运输工具数量的表达式;式(8)为s阶段对运输到达时间的限制;式(9)为第二阶段血站供应量的表达式;式(10)为各阶段灾区血站所需调剂量的表达式;式(11)为s阶段末的库存表达式;式(12)为s阶段e地血站接收血液新鲜度的表达式;式(13)为决策变量的值域约束.

3.3 需求量预测

灾害发生后,通过基本灾情信息估计伤亡人数[12],结合输血比例、人均输血量可以预测出应急救援期间的血液需求总量.在总量确定后,血制品的每日需求量可用 Logistic函数[13]预测,如式(14).在初始周期,参数φ、η通过经验数据得出,之后可以通过每日实际需求数据拟合修正模型参数.

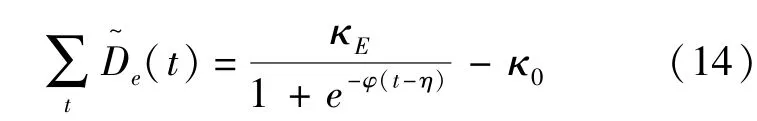
式中 φ——紧迫参数,其值越大,用血量的增长速度越快,取值区间为[0.1,1];

η——平衡参数,当t=η时单位周期的用血量增长到最大值;

κE、κ0——总量系数、初始量系数.

4 模型求解

4.1 多目标转化

上述模型是一个多目标优化问题,引进目标值权重系数ω1、ω2、ω3,且ω1+ω2+ω3=1,转化成单目标问题

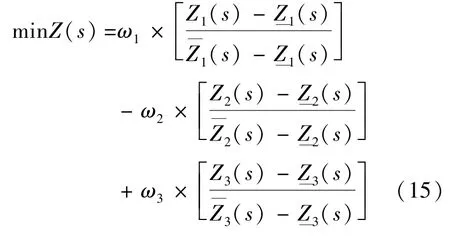
4.2 遗传—禁忌混合算法

在此设计了一种遗传—禁忌混合算法:禁忌搜索算法用来求解出救血站的选择问题;遗传算法用来解决多式运输路线优化问题,并加入局部邻域搜索操作,以加快求解的过程.

4.2.1 编码规则

为减少出救血站选择时的随机性,引入禁忌搜索策略,利用禁忌表中的信息有选择性地搜寻候选出救血站序列,以实现全局最优.选择出救候选序列X后,根据调剂需求量确定出救血站编码X′,并按运输时间约束分为:出救血站只有汽运条件集合Φ1,出救制品必须先运达其他出救血站中转成空运方式加快抵到灾区;有空运条件且必须以空运抵达灾区的出救集合Φ2;可以空运、汽运任意方式到达灾区的出救集合Φ3;只有汽运方式的出救集合Φ4.以图2为例,集合Φ1-Φ4分别为{8}、{2,3}、{4}、{6,7},设有4个受灾血站,以编号1-4表示汽运到达,其中第1、2个受灾血站有空运接收条件,以1′、2′表示空运到达.

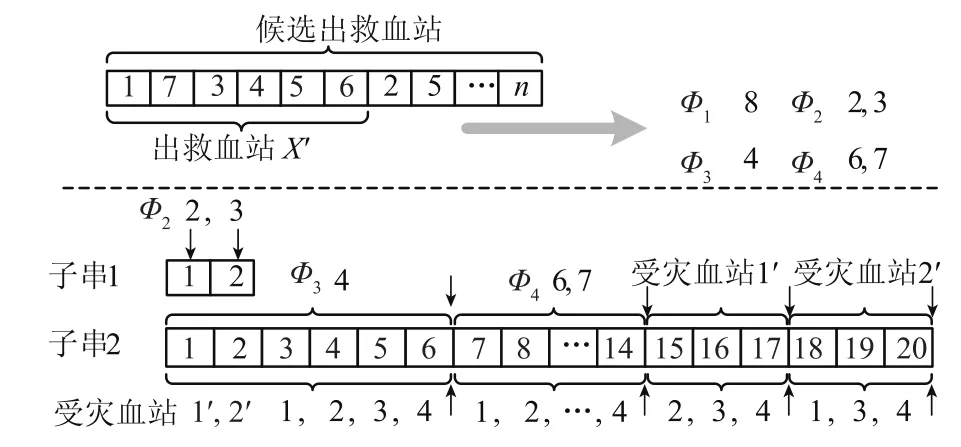
图2 编码示意图Fig.2 Schematic diagram of coding

遗传算法中的每条染色体由子串1和子串2组成.集合Φ1中血站的出救制品以汽车运达集合Φ2中的一个血站(按最近距离选取)进行中转,这一操作不需在编码中体现.子串1的长度与Φ2相同,各基因位随机取值为有空运条件的受灾血站编号.子串2中每一位编码用来表示运输出发点与接收点的对应关系.

以图2为例,Φ3中的每个血站都有6个可行接收点编码位,对应以空运到达受灾血站1、2,以汽运到达受灾血站1-4;同理,Φ4中的每个血站对应有4个可行接收点编码位.由于有血制品通过受灾血站1、2进行转运,使其也成为了出发点,分别分配给3个可行接收点编码位(第二阶段时有出救能力的血站都应分配给可行接收点编码位).通过随机方式生成一个子串2序列,从左边的第一个基因位开始,根据其值确定出发点、到达点、运输方式,当到达方式为空运时,则运输量为从该出发点应空运出的所有制品的剩余总量;当到达方式为汽运时,若出发点k血型p制品的剩余供应量与到达点此制品的缺口量(需求量与接收量之差)均大于0,剩余供应量小于缺口量时,此制品运输量在数值等于出发点的剩余供应量,否则应等于到达点的缺口数量;按此规则遍历|K|个血型|P|个制品,从而可以得出两地之间的运输总量.从左到右遍历子串2的剩余基因位并重复上述求解过程,结合子串1中的运输信息,建立起所有出救点与受灾点之间的运输路线安排,得出一个完整的调剂运输方案.

4.2.2 邻域搜索优化

在遗传进化过程中,同时进行运输合并的局部搜索操作.通过合并运输任务的方式,构造过程解的邻域空间,使调剂方案在邻域内得到进一步优化.以图3为例说明一种运输合并的构造方式,假设运输方式1为汽运,方式2为空运,初始运输安排为:出救血站①、②、③分别通过空运为受灾血站④、⑤、⑥提供救援.合并后的运输路线为:血站①、③出救的血液首先经汽运抵达血站②,与血站②的出救血液经空运一并运达血站⑤,然后通过汽运转运给血站④、⑥.若不同运输路线的运输任务合并后,目标函数值有所减小,调剂运输安排将相应修改.

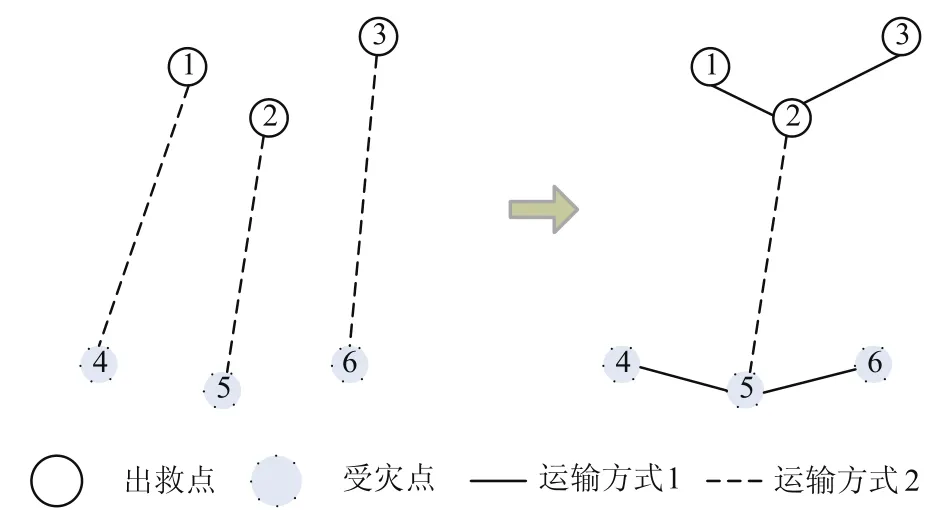
图3 合并运输示意图Fig.3 Schematic diagram of combined transportation

4.2.3 算法步骤

Step 1 确定当前阶段各个出救血站(灾区血站)的各血型各血液制品的供应量(需求量).

Step 2 初始化禁忌表G、禁忌长度tl、最大迭代次数 MaxIter,禁忌搜索邻域中候选解的个数num.并令当前最优目标值Z*=∞,iter=0.

Step 3 随机生成候选出救血站初始编码X,令X*=X.

Step 4 如果iter=MaxIter,算法停止,输出最优解编码 X*,Y*,最优值 Z*,最优调剂方案φ*;否则iter+1,转Step5.

Step 5 对X执行num次2-opt邻域操作,加入邻域N(X)中作为X的候选解集,Xi∈N(X), i=1,2,…,num.

Step 6 对N(X)中的Xi均执行以下操作.

①令gen=0,设置最大进化代数Maxgen.

②按调剂总量确定出救血站X′,根据编码规则,随机生成由子串1、2组成的染色体,重复生成pop次组成初始种群,令l=1,2,…,pop.

③以运输任务合并的方式构建染色体l的邻域解空间,进行局部搜索,得到出救点选择——运输路线安排方案φl.

④计算适应度函数值Fit(l)=Con/Z(l),其中Con为常数,Z(l)为染色体l的目标值.

⑤使用轮盘赌选择策略,按交叉率Pc对单个染色体的子串1(2)进行单点交叉、两染色体的子串1(2)进行部分匹配交叉;按变异率Pm对单个染色体的子串1(2)进行逆转变异,生成临时种群;结合精英保留策略生成新的种群.

⑥若gen＜Maxgen,gen+1,转至步骤③;否则以进化过程中求到的具有最大适应度的染色体l*对应的φl*为局部最优φi,同理Yi=l*.

Step 7 令 j=argmin(Zi),Z_now=Zj, X_now=Xj,Y_now=Yj,φ_now=φj.

Step 8 若Z_now＜Z*,Z*=Z_now,X*= X_now,Y*=X_now,φ*=φ_now,并将G中对应交换位置禁忌(赋值为tl),其它的非0项值均减1;否则根据藐视准则,释放T中值为0项的对应序列Xi,X =Xi,并将T中此项禁忌,其它的非0项值均减1,转Step4.

5 算例分析

5.1 算例构建

以“5.12”汶川大地震为背景构建算例,广州、北京等13地为当时实际出救点(编号为1-13),成都、德阳、绵阳、广元为事发地(编号为14-17).表1为各出救点的血液供应量、所供血液的新鲜度,其中λwb：λbp：λrc=1：4：5,为平时临床各制品的使用比例,各血型所占比例与所在地区人口的血型比例一致.表2为“5.12”地震后各灾区每日各血制品的实际用量,各血型制品的数量按该省人口的血型比例确定(γA：γB：γO：γAB= 0.32：0.24：0.36：0.08)[14].出救血站与灾区血站之间的运输时间与成本如表3所示.

震后72小时内为救援黄金期,绝大部分的伤员在这段时期得到搜救,医院收治伤员人数逐渐增多,临床用血量也随之增加达到高峰,设η=3、φ=0.25.假设第4天末可以确定剩余应急救援期内的用血需求量,因此第二阶段开始周期t2= 5,用式(14)可确定各情景第一阶段的调剂总量,第二阶段需求量取值为表2中的实际值.

算例其它参数设置如下:capca=1 000 U,cappl=20 000 U,θ=0.01,TU1=16 h,TU2=24 h,τ= 1 h,τdpl=3 h,τdca=1 h,C=4元,tend=15天[15].此外,算法参数设置如下:MaxIter=200,tl=50,num= 150,Maxgen=100,Pc=0.7,Pm=0.7,pop=80.

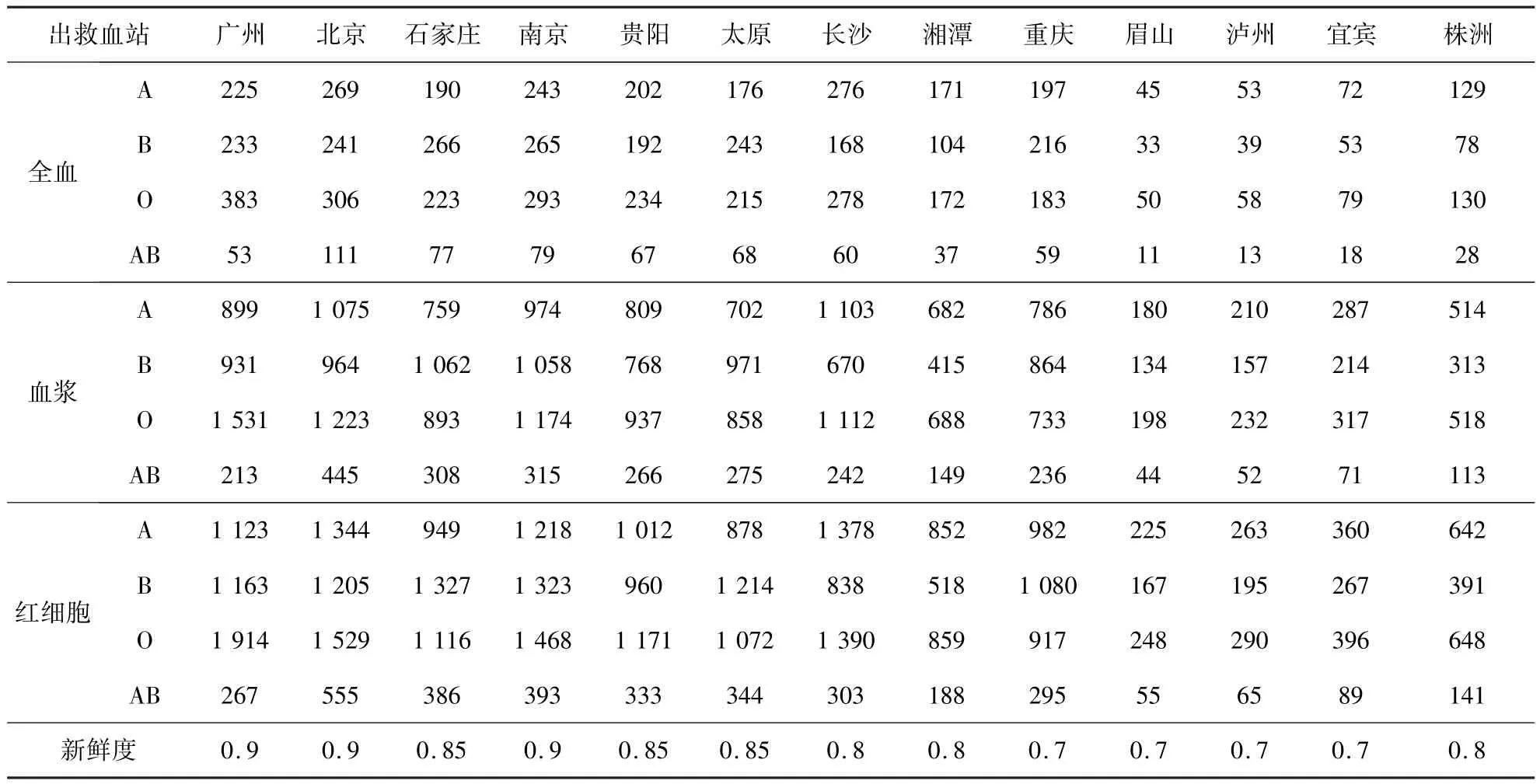
表1 出救血站血液供应量Table 1 Supply datum of retrieval blood banks (U)

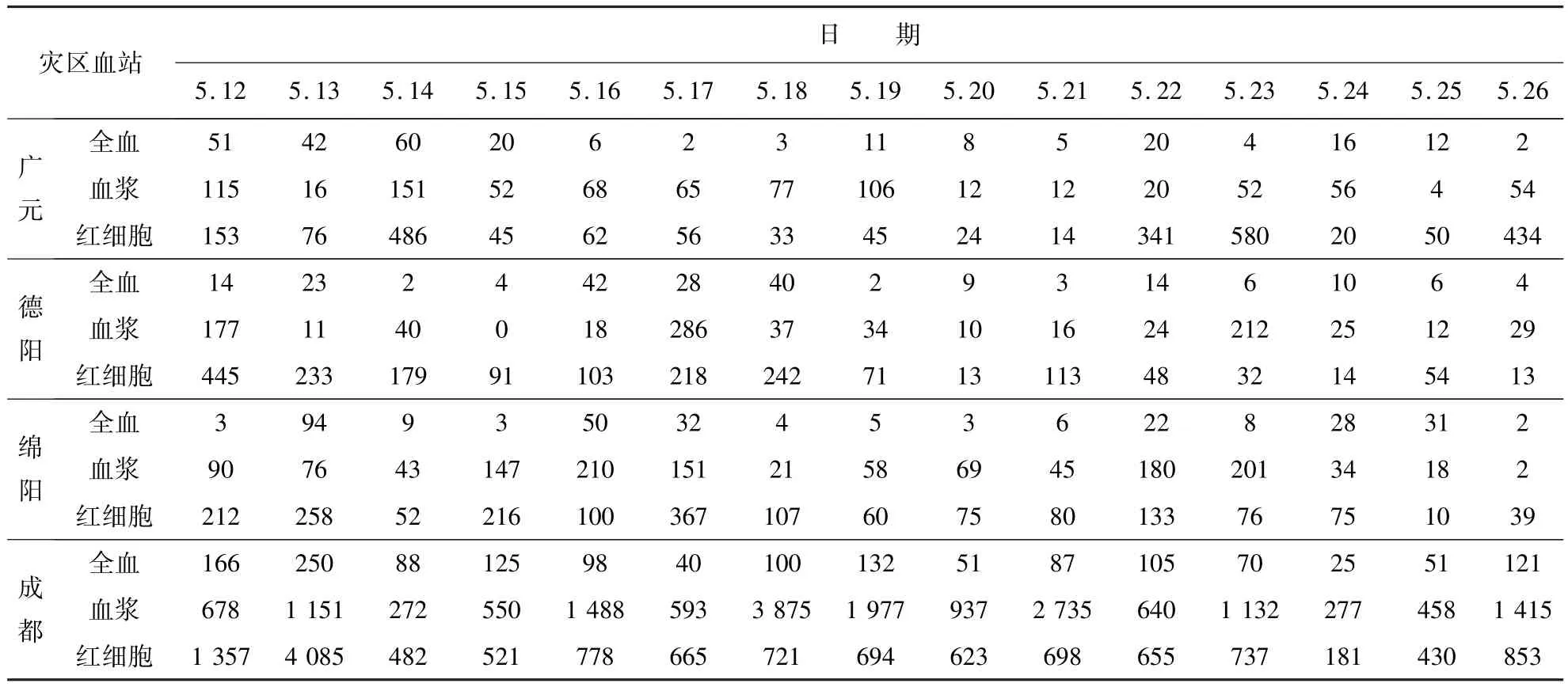
表2 灾区血站每日血液实际需求量Table 2 Actual daily blood demands of disaster areas (U)

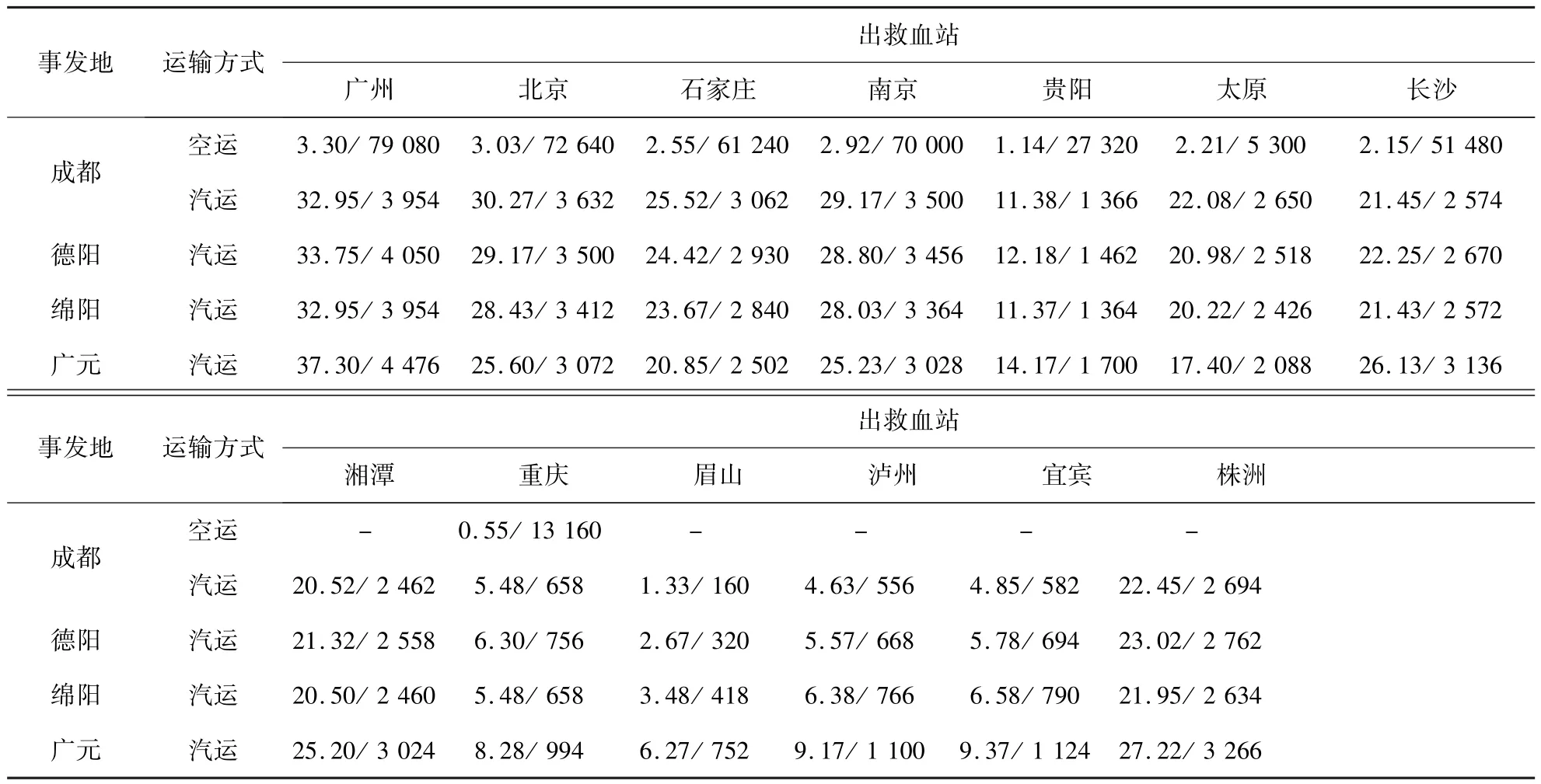
表3 出救血站至灾区血站的运输时间及成本Table 3 The transport time and cost of retrieval blood banks to the blood banks of disaster areas

5.2 结果分析

设β为血液需求总量预测误差(β＞1),即地震初始时期预测出的需求总量为应急救援期间实际总用量的β倍,变化β值得到不同的需求情景.表4为计算得出的各需求情景的两阶段调剂方案,其中‘→'表示空运,‘—'表示汽运,‘()'内为运量(U).

目标函数的权重系数选取应体现各阶段调剂决策的特征(本例中的取值如表4所示).在第一阶段决策中,因时效性要求较高,可将时间目标的权重系数设置较大,而在第二阶段各个灾区均有一定的剩余库存,对时效性的要求降低,应加大费用的权重以提高调剂方案的效益.因血液的新鲜度影响临床救治,两个阶段的权重系数均需保持一定取值.在β=1.6的情景中,若在第二阶段仍取ω1= 0.4,ω2=0.4,ω3=0.2,计算得出Z1=12.38,Z2=0.726,Z3=134 172,相比ω1=0.1,ω2=0.4, ω3=0.5时的优化结果,时间目标值减少了18.4%,运抵新鲜度增加了0.2%,但费用却增加了79.8%.可见,通过调节目标函数的权重系数可对计算结果进行优化,使调剂方案更符合决策者的预期.

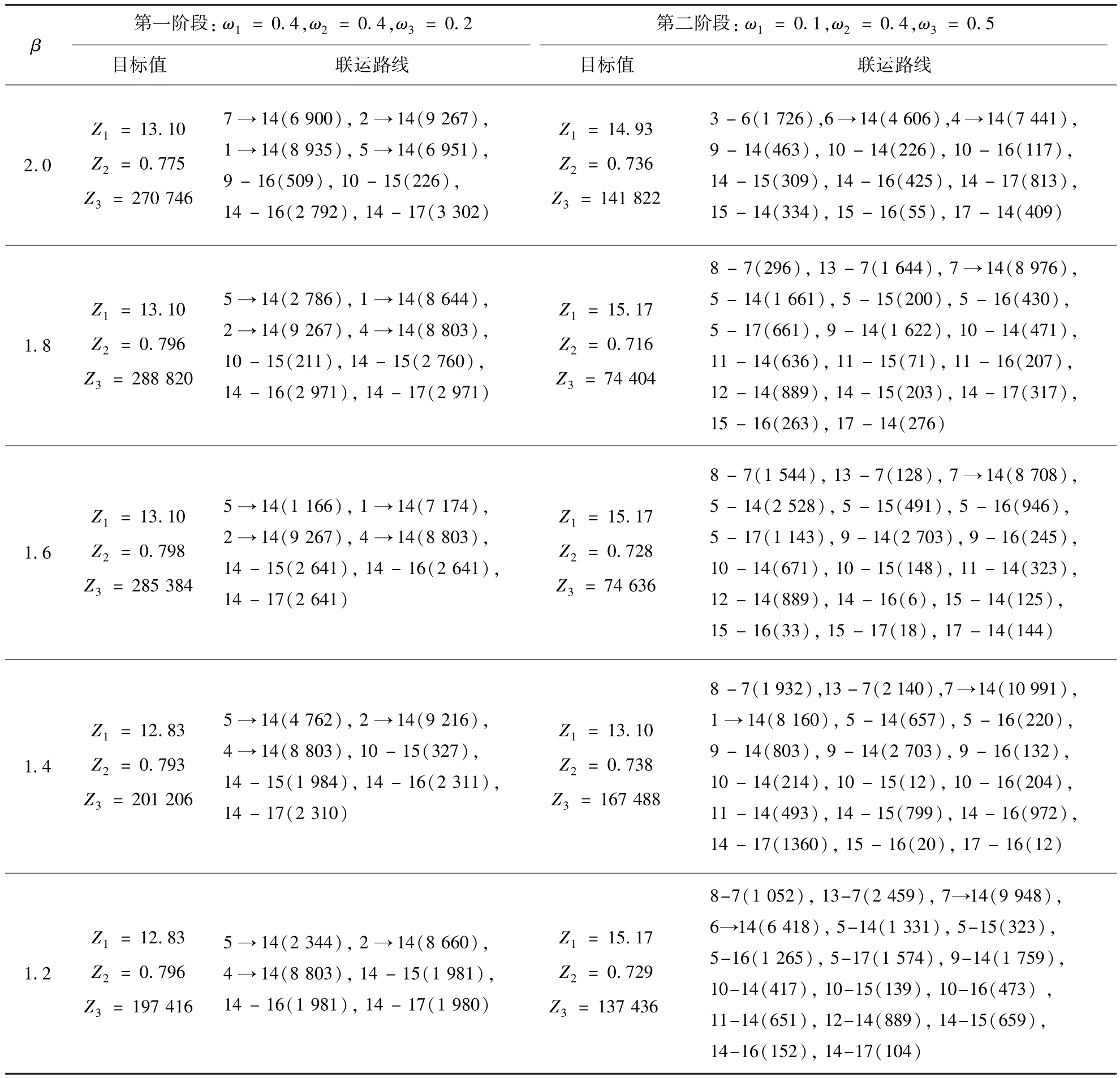
表4 不同需求情景下的两阶段调剂决策方案Table 4 The transferring solutions of two-phase in the different demand scenarios

由表4可知,在第一阶段决策中,随着β值的减小,调剂量减小,运输费用呈现减小趋势,最晚到达时间也有所下降.预测误差过大,会导致第一阶段某些受灾血站某类制品的接收量超出整个应急救援期间的用量.如β=2.0～1.4的情景中,均有由德阳或广元向成都或绵阳调剂多余库存的运输安排.此外,多式联运可以提高调剂的效率与及时性.以β=1.6时的情景为例(如图4所示),两个阶段的调剂方案都出现了多式联运安排.

现实中血液应急保障通常采用一次性决策,按初期预测量进行血液应急调剂.表5对β=1.6情景下一次性决策与两阶段决策的效果进行了比较.表5中的接收新鲜度均值指4个受灾血站接收血制品新鲜度的平均值,两阶段决策方法的最晚抵达时间为两次决策最晚抵达时间的均值,积压量指灾区血站接收的血制品在应急救援期结束后仍未出库的数量.在最晚抵达时间、接收新鲜度均值、运输费用、积压量这四个指标上,两阶段决策方法都优于一次性决策方法.即使事发后对血液需求量的预测出现一定偏差,使用两阶段决策方法都可得到较优效果的调剂决策方案.

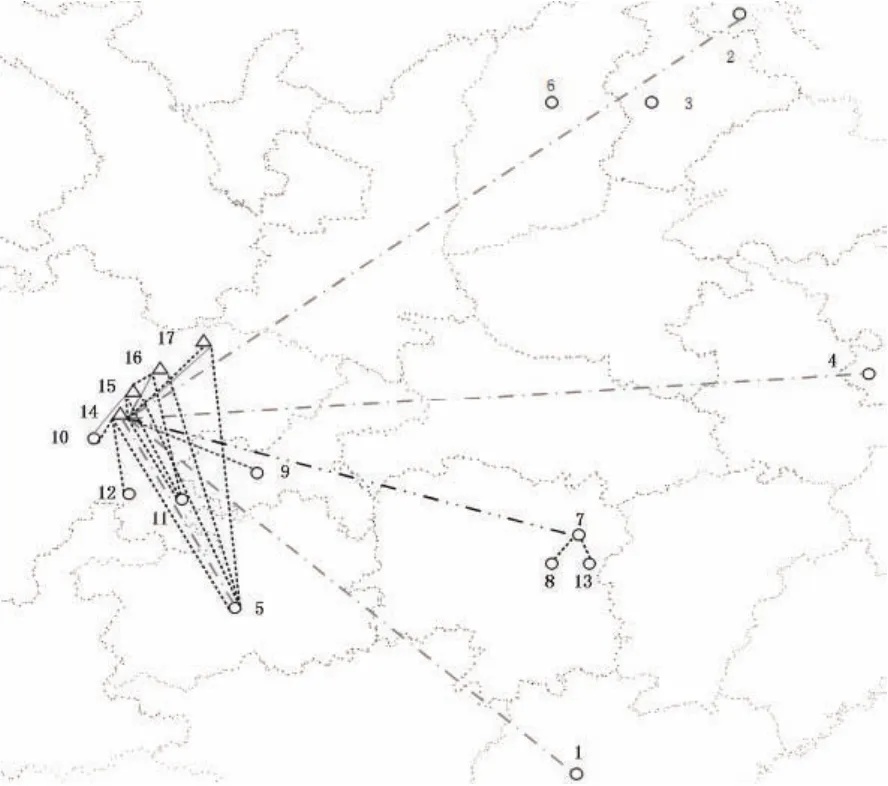
图4 两个阶段的调剂方案示意图(β=1.6)Fig.4 Schematic diagram of two-phase transferring solution(β=1.6)

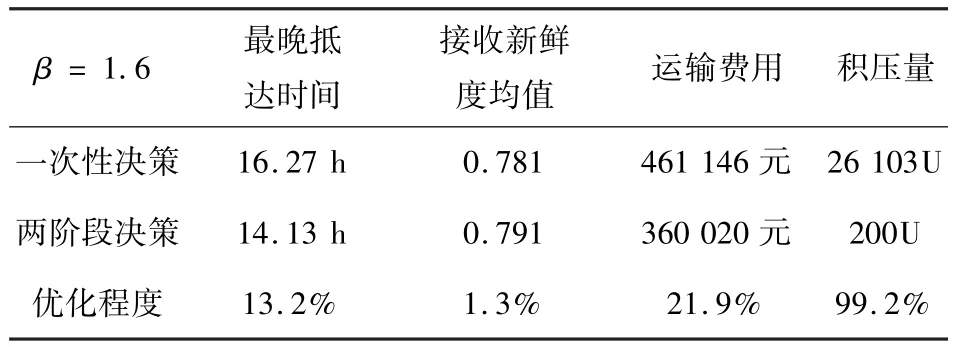
表5 两种决策方法的效果分析Table 5 Performance comparison for two decision-making approaches

6 研究结论

本文结合血液生理特性与应急保障特性,采用两阶段决策方法进行血液调剂,以最晚运达时间、血液接收新鲜度、运输费用为目标,建立了多品种、多式联运的出救点选择—运输路线安排模型,设计了包含邻域优化的遗传—禁忌混合算法进行求解,并以“5.12”汶川大地震应急血液保障为背景构建算例对模型与算法进行了验证.结果表明,两阶段决策方法在最晚抵达时间、新鲜度均值、运输总费用、血液积压量等指标上均比一次性决策优越,避免了由于血液需求预测误差过大带来的不利影响,从而为决策突发事件应急血液调剂问题提供了一个新的思路.

[1]刘春林,何建敏,盛昭瀚.应急系统调度问题的模糊规划方法[J].系统工程学报,1999,14(4): 351-365.[LIU C L,HE J M,SHENG Z H.Fuzzy programming for scheduling problem in emergency systems[J].Journal of System Engineering,1999,14 (4):351-365.]

[2]戴更新,达庆利.多资源组合应急调度问题的研究[J].系统工程理论与实践,2000,12(9):52-55. [DAI G X,DA Q L.The study of combinatorial scheduling problem in emergency systems[J].Systems Engineering—Theory& Practice,2000,12(9): 52-55.]

[3]Wang H Y,Wang X P,ZENG A Z.Optimal material distribution decisions based on epidemic diffusion rule and stochastic latent period for emergency rescue[J]. International Journal of Mathematics in Operational Research,2009,1(1/2):76-96.

[4]Haghani A,Oh S C.Formulation and solution of a multi-commodity,multi-modal network flow model for disaster relief operations[J].Transportation Research Part A:Policy and Practice,1996,30(3):231-250.

[5]Özdamar L,Ekinci E,Küçükyazici B.Emergency logistics planning in natural disasters[J].Annals of Operations Research,2004,129(14):217-245.

[7]马祖军,王绍仁.自然灾害应急物资的多阶段动态多式联运模型研究[J].中国管理科学,2009,17 (S):53-58.[MA Z J,WANG S R.A multi-stage and dynamic multi-modal transportation model for relief commodities in natural disasters[J].Chinese Journal of Management Science,2009,17(S):53-58.]

[8]Hess J R,Thomas M J G.Blood use in war and disaster lessons from the past century [J]. Transfusion,2003(43):1622-1633.

[9]王培华.输血技术学[M].北京:人民卫生出版社. 2002.[WANG P H.Blood transfusion technology [M]. Beijing: People's MedicalPublishing House,2002.]

[10]王松云,徐珊珊,吕伟珍,等.温控与运输对血液质量的影响研究[J].现代预防医学,2010,37 (19):3723-3728.[WANG S Y,XU S S,LV W Z, et al. The influence oftemperaturecontroland transportation on the quality of the blood[J].Modern Preventive Medicine,2010,37(19):3723-3728.]

[11]Nahmias S.Perishable inventory theory:A review[J]. Operations Research.1982(30):680-708.

[12]马玉宏,谢礼立.灾区震人员伤亡估算方法研究[J].灾区震工程与工程振动,2000,20(4):140-147.[MA Y H,XIE L L.Methodologies for assessment of earthquake casualty[J].Earthquake engineering and engineering vibration,2000,20(4): 140-147.]

[13]Lindell M K.An empirically based large scale evacuation time estimate model[J].Transportation Research Part A,2008(42):140-154.

[14]张钦辉.临床输血[M].上海:上海科学技术出版社,1999.[ZHANG Q H.Clinical transfusion science [M].Shanghai:Shanghai Science and Technology Press,1999.]

[15]高建国.灾区地震应急期的分期[J].灾害学. 2004,19(1):11-15.[GAO J G.Discussion on earthquake emergency response term[J].Journal of catastrophology,2004,19(1):11-15.]

A Two-phase Decision-making Approach for Emergency Blood Transferring Problem in Public Emergencies

WANG Ke-minga,MA Zu-junb,ZHOU Yu-fenga
(a.School of Traffic and Transportation;b.Institute for Logistics and Emergency Management, School of Economics and Management,Southwest Jiaotong University,Chengdu 610031,China)

Considering the physiological and emergency supply characteristics of blood,as well as multitype blood and multi-modal transportation mode,a combined optimization model for emergency service facility selection and transportation routing problem in emergency blood supply is developed based on a twophase decision-making approach.The aim is to minimize the last arrival time,maximize the lowest average freshness when

,and minimize the total transportation cost of emergency blood.A hybrid genetictabu algorithm with local neighborhood search is also proposed.The model and algorithm are verified by a numerical example based on the emergency blood supply process in‘5.12'Wenchuan earthquake in China. The results show that the advantage of two-phase decision-making approach is confirmed on the indexes such as the last arrival time,the average freshness,the total transportation cost and the overstock of blood.

logistics engineering;blood transferring;two-phase decision-making;emergency service facility selection;transportation routing

F252;C931

A

F252;C931

A

1009-6744(2013)01-0169-10

2012-07-13

2012-08-18录用日期:2012-09-04

国家自然科学基金重大研究计划项目(90924012);国家自然科学基金(70771094);教育部新世纪优秀人才支持计划资助项目(NCET-10-0706);四川省青年科技基金(09ZQ026-021);四川省学术和技术带头人培养资金项目(川人社办发[2011]441号);中央高校基本科研业务费专项资金资助项目(SWJTU11CX152).

王恪铭(1981-),男,江西浮梁人,博士生.

*通讯作者:zjma@swjtu.cn