基于认知更新的随机动态分配模型

张 玺,郭洪洋,刘海旭,李延来,蒲 云

(西南交通大学交通运输与物流学院,成都610031)

基于认知更新的随机动态分配模型

张 玺,郭洪洋,刘海旭*,李延来,蒲 云

(西南交通大学交通运输与物流学院,成都610031)

研究先进出行者信息系统(ATIS)环境下道路网络系统流量的随机动态变化,有利于实现ATIS在网络系统中的进一步优化配置.在出行者经验积累过程基础上,引入ATIS作用下的认知更新过程,将路网系统的路径流量明确视为随机变量,提出了一个基于认知更新的随机动态分配模型.证明了该模型产生的路径流量渐近收敛于一个平稳概率分布.在算例网络中验证了模型的可行性,模拟有ATIS和无ATIS两种情形下路径流量的随机动态变化.结果表明,两种情形路径流量均收敛于平稳概率分布.前者的平均流量近似于随机用户平衡(SUE),而后者的平均流量不是平衡流量,但其网络总费用要低于前者.

系统工程;随机动态分配;随机过程;道路网络;先进出行者信息系统;随机用户平衡

1 引 言

在道路网络系统中,由于交通需求和道路供给能力存在不确定性,出行者的出行决策(如出发时间选择,路径选择等)常常表现出随机性.另一方面,由于道路网络系统的开放性,有多种渠道(如交通广播、出行者间交流、可变信息标志等)可以获得路网信息,根据这些得到的信息和出行经验积累,出行者会依据利于自身的原则改变出行决策,因而从时间维度看他们的出行决策又表现出动态性.交通流是巨量出行者出行决策的集计表现,因此,道路网络系统本质上是一个随机动态系统,明确其随机特性和动态特性是较为全面地分析道路网络系统状态变化,为交通规划管理决策提供可靠依据的根本前提.

ATIS将信息技术发展的成果应用于交通系统,为出行者提供实时的、可靠的出行信息,为他们带来前所未有的便利性.在ATIS环境下,出行者的出行决策必然受到发布信息的影响,从而在宏观层面上导致路网交通流产生动态变化,为此,许多国内外交通学者从动态角度对出行者出行决策展开研究.Mahmassani等采用交互式多用户决策模拟器设计了通勤用户日常出行决策实验,发现提供信息会增加用户对行程时间变动的敏感度,他们会更频繁地改变路径选择[1].石小法建立基于出行经验和实时信息进行行程时间预测更新的动态选择模型,表明出行者经过反复出行后,其理解行程时间均值会趋于稳定[2].刘天亮等结合风险决策和认知更新建立了日常路径选择演进框架,发现信息系统误差大小会影响路径流量趋于稳定的经过时间长短[3].贺振欢等对多诱导机制共存下路径选择行为进行了模拟,总结了不同情形下诱导机制对出行者路径选择的影响[4].熊轶等依据出行者对信息系统的相信程度将用户类型进行了划分,导出了该情景下的理解路径时间函数[5].况爱武等认为不管出行者是否拥有ATIS设备,他们都不大可能准确获得路网信息,在随机用户均衡假设下建立了广义费用分配模型,表明适当的ATIS市场渗透率和信息质量能得到合理的流量分布[6].

然而,上述研究尽管明确了ATIS环境下用户出行决策具有随机动态双重特征,但出于简化问题复杂性的目的,他们往往暂时忽略其中一种特征仅就另一种特征展开研究,如此一来得出的结论必然具有片面性.因而有必要同时考虑交通系统的这两种特征,使用随机动态系统方法来描述问题. Cascetta[7]明确地将路径流量视为随机变量,提出了一类具有马尔可夫性的随机动态分配模型,在该模型框架中,路径选择概率被证明符合马尔可夫性,即当期的路径选择概率可由过去有限时期的路径选择概率确定,这暗示了用户出行决策是一个经验积累的过程.随后 Davis,Cantarella等[8,9]系统地讨论了运输网络的动态性和平衡之间的关系,他们从确定性动态过程和随机动态过程两方面入手,以交通系统的日常动态为研究对象,从理论分析和数值计算上得到一般性结论,提出了与传统数学规划算法不同的动态模拟算法.Watling和Hazelton[10,12]分别从理论上研究了随机动态模型和确定动态模型,以及传统静态分配模型之间存在的关系.

尽管他们在论述中提及了外部信息系统可能会对随机动态模型产生作用,但就目前所知,还没有具体讨论这一问题的报道.为此,本文在ATIS环境下,明确地考虑路径流量随机性和出行者基于信息系统的认知更新过程,提出一个基于认知更新的随机动态分配模型,在算例网络中验证该模型的可行性,比较了有无ATIS两种环境下路径流量的变化.

2 符号与假设

考虑道路网络G(N,A),其中节点集为N,路段集合为A.OD对集合为W,任意OD对w∈W间的有效路径集合为Kw.设OD对w∈W需求固定不变,表示为dw.路段—路径关联关系表示为0-1变量δak,当且仅当路段a∈A是路径k∈Kw的构成部分时取值为1,否则取值为0;Δw为相应矩阵形式.a表示路段a的设计通行能力;表示路段a的自由流行程时a间.离散时域L={0,1,…,M}表示研究时域,令M足够大以保证在研究时域内可以充分观察路网状态变化,本文约定离散时域中的时点n∈L表示现实中的任意一天,根据需要可以考虑一天中任意时间段的交通网络,例如高峰期间或指定时间段.

对于路网系统中的任一OD对w,设集合Sw= {0,1,2,…,dw}为路径流量的样本空间,建立在Sw上的离散随机变量(kn)表示第n天路径k上的流量,(wn)为向量形式,则随机过程w= {(w0),(w1),…,(wM)}表示该OD对w间路径流量随机动态变化;x(an)表示第n天路段a上的流量,x(n)为向量形式,根据路段—路径关联关系有x(n)= Δw(wn),实际上路段流量是随机路径流量的函数;设路段费用为路段流量和通行能力的函数表示为t(an)= τa(x(an),a);T(kn)表示路径费用,根据路段—路径关联关系有T(kn)=Σa∈Aδakt(an);V(kn)表示路径可测负效用,V(wn)为向量形式;路径选择概率函数为P(kn)=Pk(V(wn)),P(wn)为向量形式.

3 效用更新和路径选择

实际道路环境由于受到交通事故、天气、道路改造及维护等随机因素的影响,出行者在出行前不大可能掌握整个路网物理结构及路段费用等相关信息.经过反复地出行决策后,出行者会积累相当的出行经验并逐渐熟悉路网环境.因此,基于这些过往经验,出行者对当前路网建立了一定的认知,据此作为他们实施出行决策的依据.

3.1 效用更新学习

路径选择是出行决策中一个重要的环节.目前,基于随机效用最大化的离散选择模型能够比较好的描述这一决策环节.为了描述出行者过往出行经历对当前认知的影响,需明确引入具有指数下降权重线性加权的学习机制[12],第n天路径k∈Kw的可测负效用表示如下

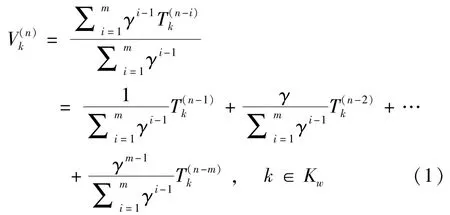
式中 m表示有效经历的长度或有效记忆长度,解释为出行者基于最近m天的经历形成当前认知;γ为学习参数,为学习权重,表示过去出行经验对当前认知的影响程度,从时间上来看,过往经历距离当前时间越近,其影响程度越大.

由于出行者之间存在个体差异,他们对路径效用的认识并不一致,这种不一致性可通过随机效用误差描述,因此路径k的随机负效用V～(n)k表示为

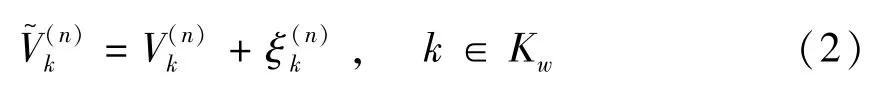
式中 ξ(kn)表示出行者之间存在的理解误差,假设服从均值为0、方差为σ(n)的独立Gumbel分布,可见该分布的方差与时间有关.

3.2 理解误差更新

随着信息工程相关技术的发展,ATIS能够提供较为全面的路网信息,但由于测量、设备和其他等因素,ATIS发布的信息并不一定能够准确地描述当前路网的实际情况,换言之,发布的信息存在一定的误差.因此,本文假设信息误差ζk服从均值为0、方差为φ的独立正态分布.

出行者借助ATIS的信息支持和出行经验积累,他们对出行环境的认知程度将逐渐趋于一致,从数学语言角度来看,这表示理解误差的方差将随着时间推移不断减小.这一过程可表示为如下递归方程式[3,13]

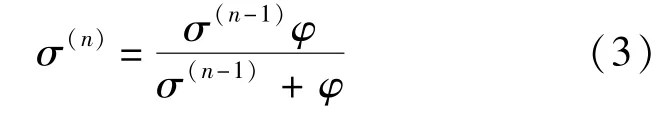
式中 φ表示ATIS所提供信息的是误差方差,本文中假设不随时间变化;σ(n)表示出行者的理解误差方差,假设随时间推移而变化。

3.3 路径选择过程

根据离散选择理论,理解误差服从Gumbel分布时,路径选择概率为Logit概率函数

式中 θ(n)为Gumbel分布的参数,与方差的关系为

从式(4)可以看到,OD对w间有效路径集Kw的选取会影响路径选择概率,不同的有效路径集表现不同的路径选择准则,从而产生不同的流量分配结果.由无环简单路径构成的有效路径集不仅能避免环形路径,而且能够保证潜在可选路径的完整性,具有理论和实际意义.因此本文选取全部的无环简单路径作为有效路径,并采用分层算法[14]确定有效路径集.分层算法为遍历算法,路网中的每条路段和每个节点至少被访问一次,因而最后能够列出所有有效路径,得到每个OD对的路段—路径关联矩阵Δw.

随着认知程度加深,随机理解误差的方差将不断减小,但理解误差不可能完全消除,出行者的出行决策仍然表现出一定的随机性,那么路网中由大量个体出行者集计而成的交通流也表现出随机性,路网系统可视为一个随机动态系统.对路网中每个OD对w而言,出行者根据路径负效用从有效路径集合中选择路径,将所有出行者的选择结果进行集计可得到,第n天路径k随机流量的概率分布实际上是过去m天路径k流量给定情况下的条件分布,该分布可以近似为以OD需求dw和选择概率向量P(n)为参数的条件多项分布 (MultinomialwDistribution)[12]

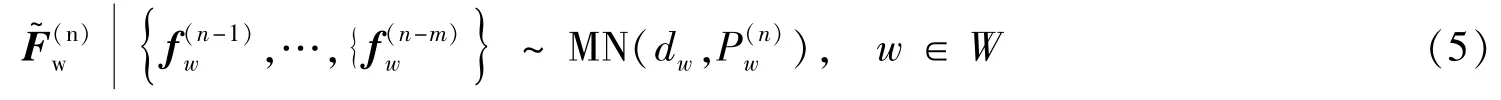
4 随机动态分配模型

综合上述分析,参考文献[7],给出基于认知更新的随机动态分配模型.

命题随机过程存在唯一的平稳概率分布.

证明:在研究时域内,路径选择概率满足

(1)时齐性;

(2)由Logit选择概率函数保证任意有效路径选择概率不为零;

(3)路径选择概率依赖于有限个过去状态.

因此,直接应用文献[7]中的命题A和命题B得出结论,证毕.

由命题1可知,路网系统随着时间推移能够收敛到唯一的平稳概率分布.式(6)实际上表示了第n天路段流量为过去所有流量的算数平均值,这表明随机动态分配模型的流量加载过程类似于相继平均算法(MSA)的步骤.因此,参考MSA给出详细的分配步骤如下:

步骤1初始化.设定参数γ,m,M,φ, σ(0),令n=0,设任意OD对从多项分布中使用随机向量发生器生成路径流向量f(0)w,根据路段—路径关联性得到初始路段流向量x(0)=Δw(0)w.

步骤2更新认知误差方差.令n=n+1,使用式(3)更新 σ(n),然后得到离差参数 θ(n)=

步骤3更新理解路径费用.计算路段费用如果n≤m,令理解路径费用为如果n＞m,使用式(1)更新理解路径费用.

步骤4生成随机路径流量.对于每对OD对w,将V(kn)代入式(4)得到路径选择概率P(kn),然后使用随机向量发生器从多项分布(wn)～MN(dw,P(wn))中生成随机路径流向量f(wn).步骤5更新路段流量.将f(wn)和x(an-1)代入式(6),得到新的路段流量x(an).

步骤6检查停止条件.如果n=M,停止分配过程,否则返回步骤2.

5 算例分析

算例网络[4]有9个节点,12条路段,一个OD对,如图1所示.OD需求设为dOD=500 veh·h-1,路段能力和路段自由流费用等参数见文献[4],本文不再列出.路段费用函数为常用的BPR函数,其他参数设定如下:初始认知误差标准差0.33 h,不随时间变化的 ATIS信息误差标准差有效记忆长度m=3 d,学习参数为γ=0.3,总天数为M=100 d.

为了比较ATIS发布信息对出行者认知更新的影响,本文分别考虑了存在和不存在ATIS两种情形下路网系统路径流量的随机动态变化.算例网络共有6条有效路径,现考察路径1-4-7-8-9和路径1-2-5-6-9两条路径的流量在有无ATIS情形下的变化情况,图2给出了两条路径流量在两种情形下的样本轨迹.

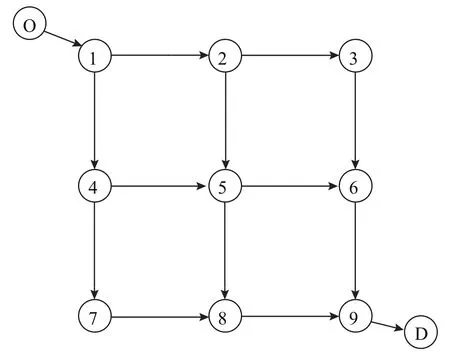
图1 算例网络Fig.1 Example network

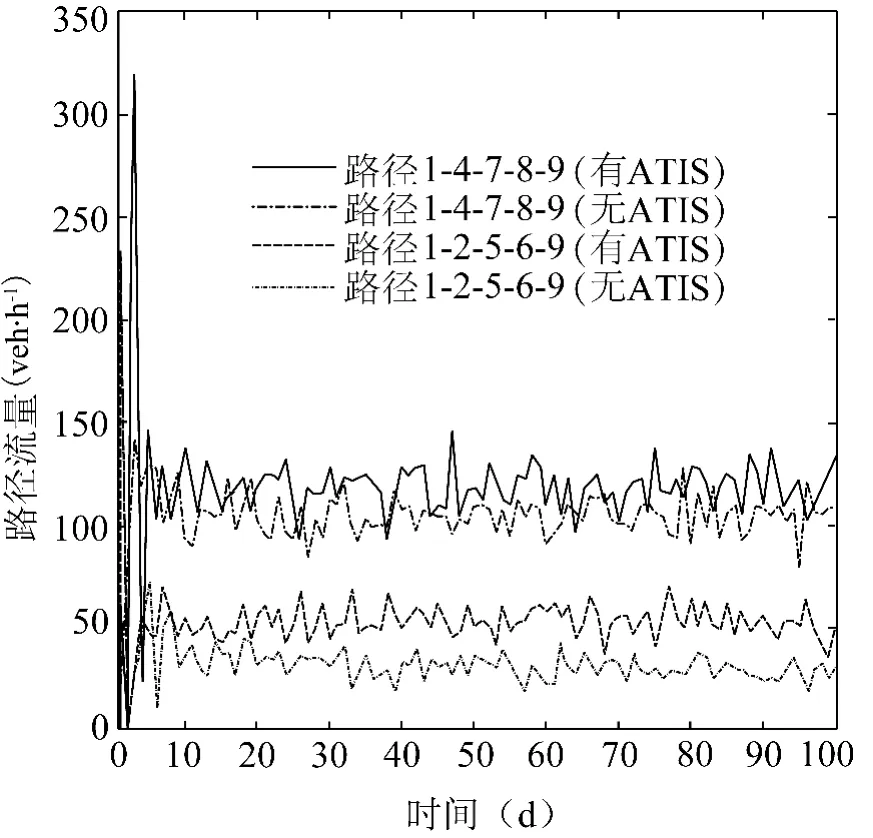
图2 路径流量变化Fig.2 Flow variation of route

可以看到,无论是在有ATIS或无ATIS情况下,两条路径的流量在第十天之后均表现出收敛行为.为了进一步考察路径流量在时域内的平均变化情况和波动程度变化情况,分别对有ATIS和无ATIS情形下的路网进行1 000次随机动态分配,得到两种情形下共2 000个样本轨迹,并分别统计了路径流量的期望和标准差随时间变化的情况,如图3、图4所示.路径流量期望值和标准差同样也在第十天后随时间推移收敛到稳定值,从统计上来看,经过一段时间后,路径流量概率分布的一阶矩和二阶矩均趋于稳定,这说明路径流量收敛于一个平稳概率分布,例如路径1-4-7-8-9的路径流量在有ATIS情形下收敛于期望为117.814 1 veh·h-1、标准差为10.551 0 veh·h-1的概率分布,而在无ATIS情形下收敛于期望为104.291 1 veh·h-1、标准差为9.138 2 veh·h-1的概率分布.

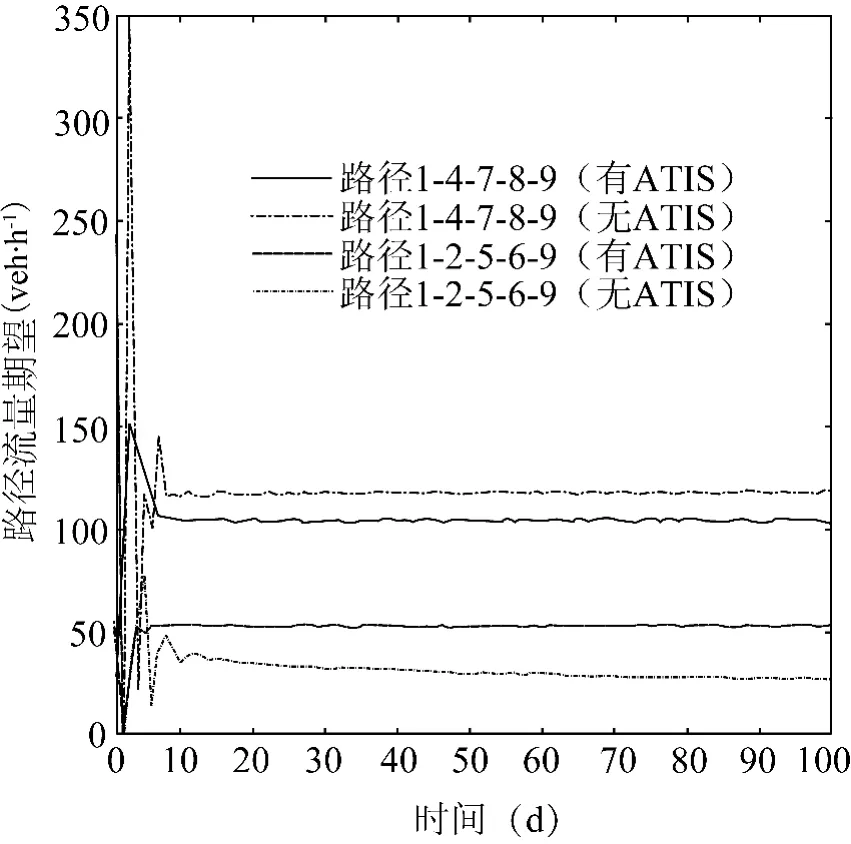
图3 路径流量期望变化Fig.3 Expectation variation of route flow

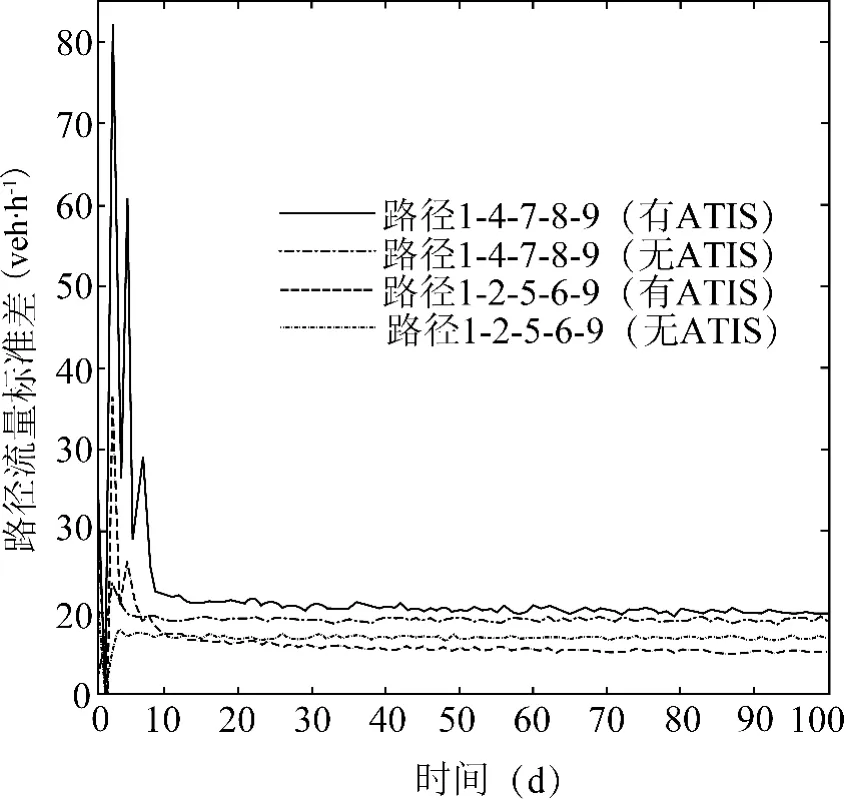
图4 路径流量标准差变化Fig.4 Standard deviation variation of route flow

为了考察两种情形下各路径流量和行程时间平稳状态下的平均水平,取第10天到第100天的数据求算数平均值,结果汇总如表1所示.发现,当有ATIS发布信息时,各路径的行程时间差不多约为1.24 h,这表明随机路径流量的平均值近似于SUE流量.然而,在无ATIS情形下,路径1-4-7-8 -9、路径1-4-5-8-9和路径1-2-5-8-9的行程时间反而比有 ATIS情形下的行程时间减少约0.04～0.06 h,而其他路径的平均流量虽然有所增加或减少,但相应的行程时间并没有明显变化.两种情形的路网系统总费用如图5所示,有ATIS的路网总费用在平稳状态下约为620.83 h,而无ATIS的路网总费用约为605.97 h.可见,前者的总费用要高于后者14.86 h左右,这说明尽管ATIS发布信息有助于提高了人们出行的方便性和获取信息的公平性,但相应的代价是在某种程度上降低了道路交通系统的使用效率.

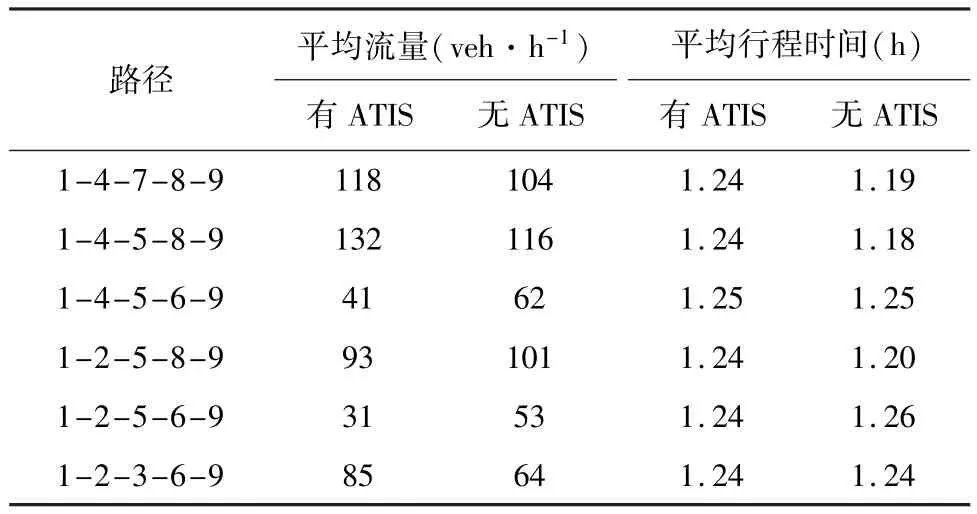
表1 路径平均流量和平均行程时间Table 1 Average route flows and travel time

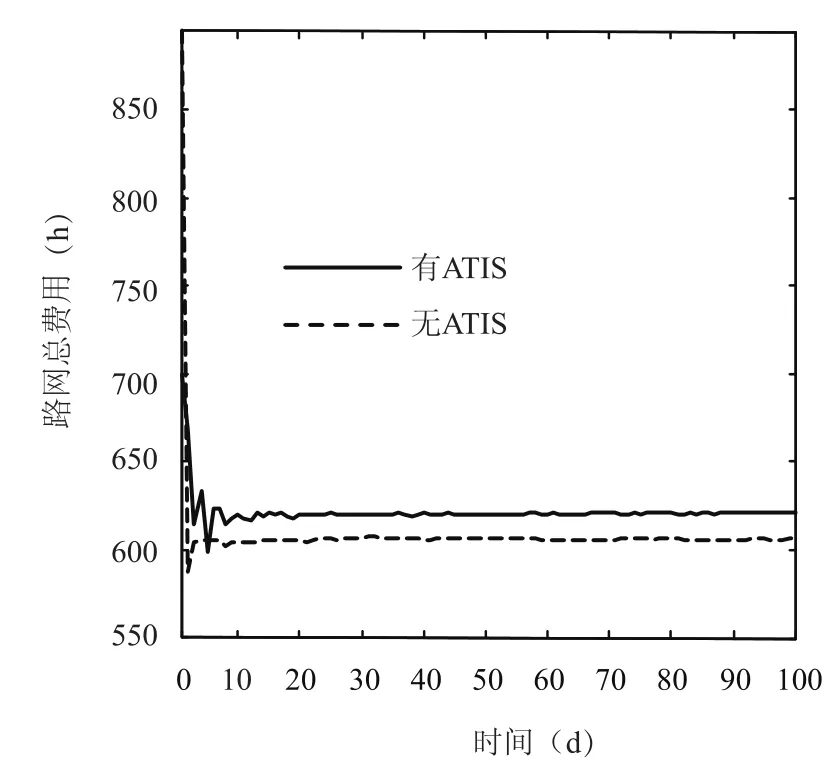
图5 路网总费用Fig.5 Network total cost

6 研究结论

ATIS提供可靠、全面的路网出行信息,提高了出行者对当前出行环境的认识,便于他们根据自身需求作出出行决策.由于交通系统的开放性,需求和供给表现出不确定性,这导致出行者即使在ATIS提供支持信息下也不大可能完全了解当前的路网状态,但他们可以通过经验积累逐渐加深对路网状态的认识.为此,本文分析了出行者的经验积累过程,基于ATIS作用下的认知更新,将路径流量明确地视为随机变量,提出了一个随机动态分配模型描述ATIS环境下的路网流量随机动态变化.在算例中发现,无论有无ATIS的环境下,路径流量均很快地收敛到一个平稳概率分布.特别地,在有ATIS时,平稳概率分布的均值近似SUE路径流量;无ATIS情形下,有三条路径的平均行程时间小于有ATIS情形,而且尽管另外三条路径的平均流量相比有ATIS情形下有所增减,但相应的平均行程时间并没有太大变化,而从网络总费用来看,前一种情形要高于后一种.这表明ATIS发布信息有助于提高人们出行的方便性和获取信息的公平性,但在一定程度上牺牲了交通系统的效率.因而从社会经济系统可持续发展层面来看,无论是交通技术的引进或是交通管理规则的实施均应当兼顾信息公平与系统效率,以保证道路交通系统对社会经济系统发展的有效支持.

[1]Mahmassani H S,Liu Y H.Dynamics of commuting decision behavior under advanced traveler information systems[J].Transportation Research C,1999,7(2-3):91-107.

[2]石小法.ATIS环境下动态选择模型的研究[J].系统工程学报,2002,17(3):271-276.[SHI X F. Study on dynamic choice model for ATIS[J].Journal of Systems Engineering,2002,17(3):271-276.]

[3]刘天亮,黄海军,陈剑.考虑风险规避和认知更新的日常择路行为演进[J].交通运输工程学报, 2008,8(4):90-94.[LIU T L,HUANG H J,CHEN J.Evolution ofday-to-dayroutechoice behavior considering risk aversion and perception updating[J]. Journal of Traffic and Transportation Engineering, 2008,8(4):90-94.]

[4]贺振欢,杨肇夏,承向军,等.ATIS混合诱导模式下出行者路径选择仿真研究[J].系统仿真学报, 2009,21(22):7334-7337.[HE Z H,YANG Z X, CHENG X J,et al.Research on users'route choice under mixed-guidance mode of ATIS by simulation[J]. JournalofSystem Simulation, 2009, 21(22): 7334-7337.]

[5]熊轶,黄海军,李志纯.交通信息系统作用下的随机用户均衡模型与演进.交通运输系统工程与信息,2003,3(3):44-48.[XIONG Y,HUANG H J,LI Z C.A stochastic user equilibrium model under ATIS and its evolutionary implemention[J].Journal of Transportation Systems Engineering and Information Technology,2003,3(3):44-48.][6]况爱武,黄中祥,张生.ATIS影响下基于广义出行负效用的随机分配[J].系统工程,2010,28(10): 108-113.[KUANG A W,HUANG Z X,ZHANG S. Stochastic assignment model based on generalized travel disutility under ATIS[J].Systems Engineering,2010, 28(10):108-113.]

[7]Cascetta E.A stochastic process approach to the analysis of temporal dynamics in transportation networks[J]. Transportation Research Part B:Methodological,1989, 23(1):1-17.

[8]Davis G A,Nihan N L.Large population approximations of a general stochastic traffic assignment model[J]. Operations Research,1993,41(1):169-178.

[9]Cantarella G E,Cascetta E.Dynamic processes and equilibrium in transportation networks: Towards a unifying theory[J].Transportation Science,1995,29 (4):305-329.

[10]Watling D.Asymmetric problems and stoch-astic process models of traffic assignment[J].Transportation Research Part B:Methodo-logical,1996,30(5): 339-357.

[11]Hazelton M L.Day-to-day variation in Markovian traffic assignment models[J].Transportation Research Part B: Methodological,2002,36(7):637-648.

[12]Hazelton M L,Watling D P.Computation of equilibrium distributions of Markov traffic-assignment models[J]. Tran-sportation Science,2004,38(3):331-342.

[13]Jha M,Madanat S,Peeta S.Perception updating and day-to-day travel choice dynamics in traffic networks with information provision [J]. Transportation Research Part C:Emerging Technologies,1998,6 (3):189-212.

[14]李志纯,黄海军.随机交通分配中有效路径的确定方法[J].交通运输系统工程与信息.2003,3(1): 28-32.[LI Z C,HUANG H J.Determining the efficient paths in stochastic traffic assignment[J].Journal of Transportation Systems Engineering and Information Technology,2003,3(1):28-32.]

Perception Updating Based Stochastic Dynamic Assignment Model

ZHANG Xi,GUO Hong-yang,LIU Hai-xu,LI Yan-lai,PU Yun
(School of Transportation and Logistics,Southwest Jiaotong University,Chengdu 610031,China)

Traffic network systems endogenously display both stochasticities and dynamics with vehicle flows formed from aggregated travelers in response to their previous experiences and the information provided by Advanced Traveler Information Systems(ATIS).In consideration of the day-to-day trip-making decisions of travelers,a perception-updating-based stochastic dynamic assignment model is proposed to describe the evolution of the traffic network flow pattern.In this model,the route flows are treated explicitly as random variables and the distribution of them is proved to asymptotically converge to a stationary probability distribution.A simulation algorithm is developed for implementing the model.Numerical results under two scenarios,with and without ATIS,are also provided for comparing the stochastic dynamics of route flows.

system engineering; stochastic dynamic assignment; perception updating; road network;ATIS

U491

A

U491

A

1009-6744(2013)01-0118-06

2012-09-18

2012-11-08录用日期:2012-11-20

国家自然科学基金项目(50908196,51278429);中央高校基本科研业务费专项资金(SWJTU09CX041).

张玺(1982-),男,重庆人,博士生.

*通讯作者:hxliu@home.swjtu.edu.cn.