基于提升小波变换的GPS动态滤波新算法
李红连,方 红,唐 炬,张 军
(1.成都大学电子信息工程学院,成都610106;2.重庆大学电气工程学院,重庆400044; 3.重庆工商大学商务策划学院,重庆400067)
基于提升小波变换的GPS动态滤波新算法
李红连*1,2,方 红1,唐 炬*2,张 军3
(1.成都大学电子信息工程学院,成都610106;2.重庆大学电气工程学院,重庆400044; 3.重庆工商大学商务策划学院,重庆400067)
针对应用卡尔曼滤波器进行车辆GPS导航信号的动态滤波时难以建立精确的数学模型,以及传统小波变换在实时性方面存在不足,提出了基于提升小波变换的GPS动态滤波新算法.该算法采用提升小波变换对车辆GPS导航信号进行分解;用3σ准则和多项式插值方法对各层提升小波变换系数进行粗差探测与数据修复;采用模平方软阈值去噪算法对各层提升小波变换系数进行去噪;最后进行提升小波逆变换,从而实现车辆GPS导航信号的动态滤波.仿真实验结果表明,该算法的导航定位精度优于卡尔曼滤波算法;虽然在导航定位精度方面稍比传统小波变换算法的性能高,但比传统小波变换算法速度快一倍;显然该算法对车辆GPS导航系统是有效的.
智能交通;动态滤波;提升小波变换;车辆GPS导航系统;3σ准则
1 引 言
全球定位系统(Global position system,GPS)是利用导航卫星进行定位,能够迅速、准确、全天侯地提供3维位置、速度和时间信息;具有定位误差不随时间积累、定位精度高、使用成本低等优点[1-4],在车辆导航系统中得到了广泛的应用.
民用导航型GPS接收机一般采用C/A码伪距测量,单点实时定位精度较低(大约30m),不能满足车辆导航定位的要求.为了提高导航定位精度,出现了各种GPS动态滤波技术.房建成、万德钧等人研究发现GPS动态定位滤波中的x、y、z分量之间没有耦合,将卫星钟差、星历误差、对流层和电离层的附加延时误差、多路径效应、接收机钟差和噪声等各种误差的影响等效为一个总误差,利用分散卡尔曼滤波器对各分量进行单独动态滤波处理,降低了系统运算量和提高了滤波速度[1,3].随着研究的深入,发现应用卡尔曼滤波器进行动态滤波时需建立精确的数学模型(即系统模型和观测模型),对于车辆等高速运动的载体来说有时是比较难以建立的.李红连等[3,4]在熊永良、黄丁发等[5]采用传统小波变换进行GPS基线求解的基础上提出了离散小波变换、平稳小波变换等传统小波变换方法进行GPS动态滤波取得了成功.郭秋英、胡振琪[6]采用传统小波变换方法也实现了GPS快速精密定位.
提升小波变换(lifting wavelet transformation, LWT)是Wim Sweldens博士提出的使用提升模式构造小波函数的一种小波变换方法,具有算法结构简单、占用内存少、速度特别快等优点,克服了传统小波变换在计算上的复杂性、运算速度无法满足实时性要求的不足[7-9].于是,本文尝试应用提升小波变换进行车辆GPS导航信号的动态滤波处理,并与卡尔曼滤波、传统小波滤波技术进行比较,为车辆GPS导航系统的开发提供新思路.
2 提升小波变换动态滤波算法
2.1 提升小波变换理论
提升小波变换属于第二代小波变换方法;不依赖于付氏变换,小波函数也不再由函数的平移和伸缩而产生,所有的运算都在时域上进行;相应于传统小波变换的Mallat算法的是对原始信号的偶数序列和奇数序列进行逐次提升和对偶提升,不仅减少了计算量,还可以实现原位计算[5-7].
提升小波变换的分解过程分为分裂、预测和更新3个步骤完成[7,8]:
Step 1 分裂是将原始信号序列si分解为偶序列si-1和奇序列di-1.
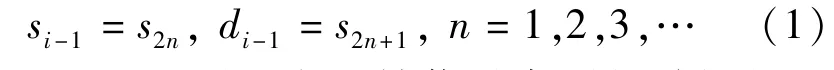
Step 2 预测是在原始信号序列相关性的基础上用偶序列si-1预测奇序列di-1,通过计算式(2)的预测误差来代替di-1.预测误差又称为细节系数或提升小波变换系数,细节系数越小,预测越精确.

式中 P为预测算子.
Step 3更新是将更新算子作用于细节系数di-1并叠加到偶序列si-1来更新偶序列si-1得到近似信号.近似信号又称为提升小波变换的尺度系数,其计算公式为
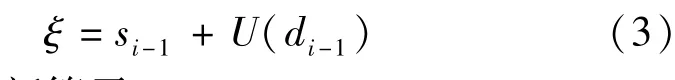
式中 U为更新算子.
重复以上3个步骤就可以实现多尺度、多分辨率的提升小波变换.
提升小波变换的重构过程(逆变换)可以直接反转实现,由反更新、反预测和合并 3个步骤完成[7,8]:
Step 1反更新是在给定 si-1和 di-1的基础上,计算式(4)就可恢复偶序列s2n.
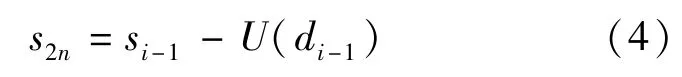
Step 2反预测是在所得的偶序列s2n和给定的di-1的基础上,通过计算式(5)就可反预测奇序列 s2n+1.
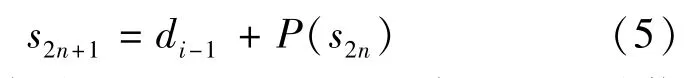
Step 3合并是由s2n和s2n+1融合得到原始信号序列:
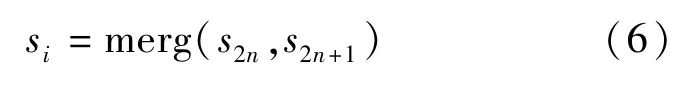
由上可知,提升小波变换的逆变换只是提升格式小波变换的简单逆向变换,不像传统小波变换的滤波器需要满足精确重构条件;所以提升小波变换比传统小波变换操作简单,易于实现;其分解和重构过程如图1所示[7-9].
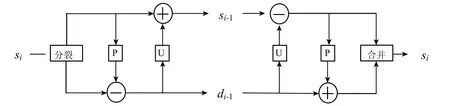
图1 提升小波变换的分解与重构过程Fig.1 Decomposition and reconstruction process of lifting wavelet transformation
2.2 粗差探测原理
由于陆地车辆运行的机动性非常强和周围环境复杂,接收到的GPS导航信号含有噪声甚至粗差;于是假设车辆在 x方向从坐标原点开始以15 m/s行使640 s,接收的GPS信号含有15 m的白噪声,并且240 s时出现一个250 m的粗差干扰来进行车辆GPS导航信号的模拟.
图2是采用提升格式改造的db3小波来对模拟的车辆GPS导航信号进行3尺度分解提升小波变换的结果.分析该结果可以发现:在粗差点邻域范围内提升小波变换系数的值,远远大于正常点范围内提升小波变换系数的值.根据这一分析结果,本文将远远大于正常范围内提升小波变换系数的点看作粗差点,剔除其值并利用周围点的系数进行内插[3-5],从而实现消除车辆 GPS导航信号的粗差.
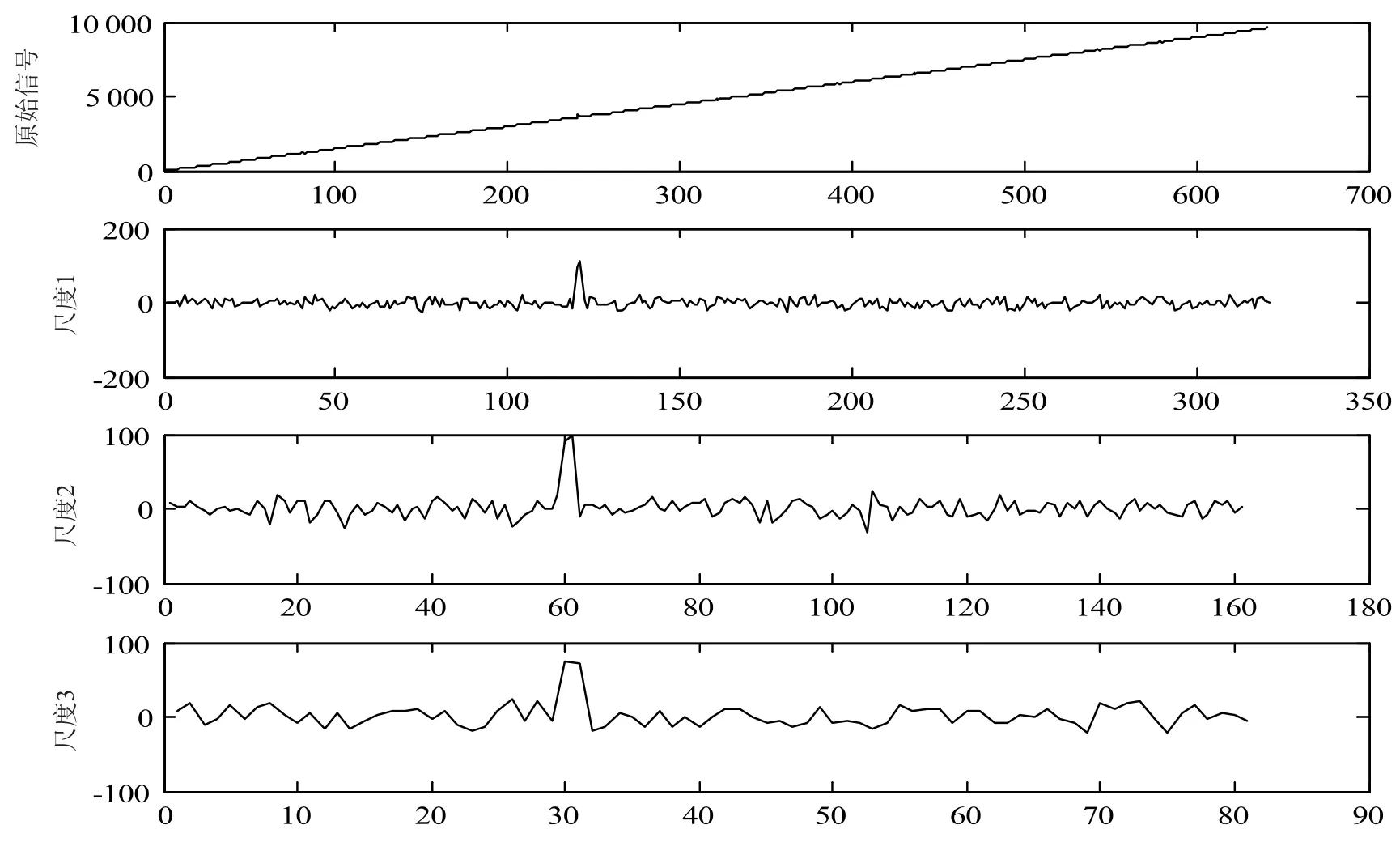
图2 含有粗差的车辆GPS导航信号的提升小波变换Fig.2 Lifting wavelet transformation for vehicle GPS navigation signal with gross error
2.3 GPS动态滤波新算法
根据以上采用提升小波变换对车辆GPS导航信号进行分解的结果和硬阈值法、软阈值法及其改进算法等去噪算法的特点,可得到基于提升小波变换的车辆 GPS导航信号的动态滤波新算法[3-5,10]:
Step 1 对车辆GPS导航信号进行多尺度的提升小波变换,得到提升小波变换系数dj,k;
Step 2 利用经验公式(7)计算各尺度的提升小波变换系数的均方根误差,对绝对值大于3σj(99.7%的置信水平)的各尺度的提升小波变换系数点确定为粗差点(3σ准则),剔除其值并利用周围提升小波变换系数采用多项式插值法(二次多项式)进行内插修改粗差点的提升小波变换系数,从而去除车辆GPS导航信号的粗差.
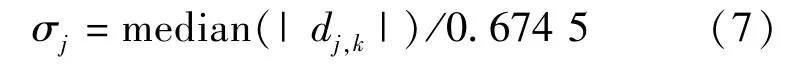
Step 3利用经验公式(8)计算各尺度的提升小波变换系数的阈值,通过模平方软阈值去噪算法估计并修改各尺度的提升小波变换系数d^j,k,其计算公式为
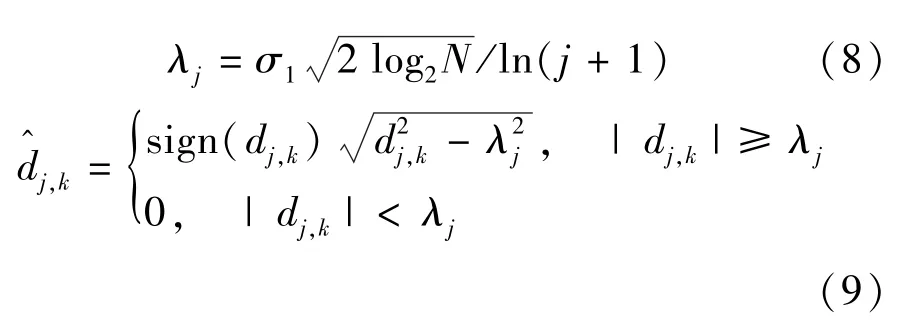
Step 4对已去噪的GPS导航信号的提升小波变换系数进行重构(逆变换),便可获得精确的车辆GPS导航信号,从而实现车辆的精确导航定位.
3 仿真实验
根据陆地车辆行驶的实际情况和GPS接收机的各个坐标分量相关性不大的特点,仿真实验以x方向为例,得到的仿真实验结果也可以用于y方向.假定车辆在x坐标分量以15 m/s速度的向前行驶,共行驶800 s,采样周期1 s;为了考察基于提升小波变换的GPS动态滤波新算法的去噪和粗差探测能力,整个信号过程加入均方根误差为11 m的白噪声以及在400 s加上70 m的脉冲干扰信号.
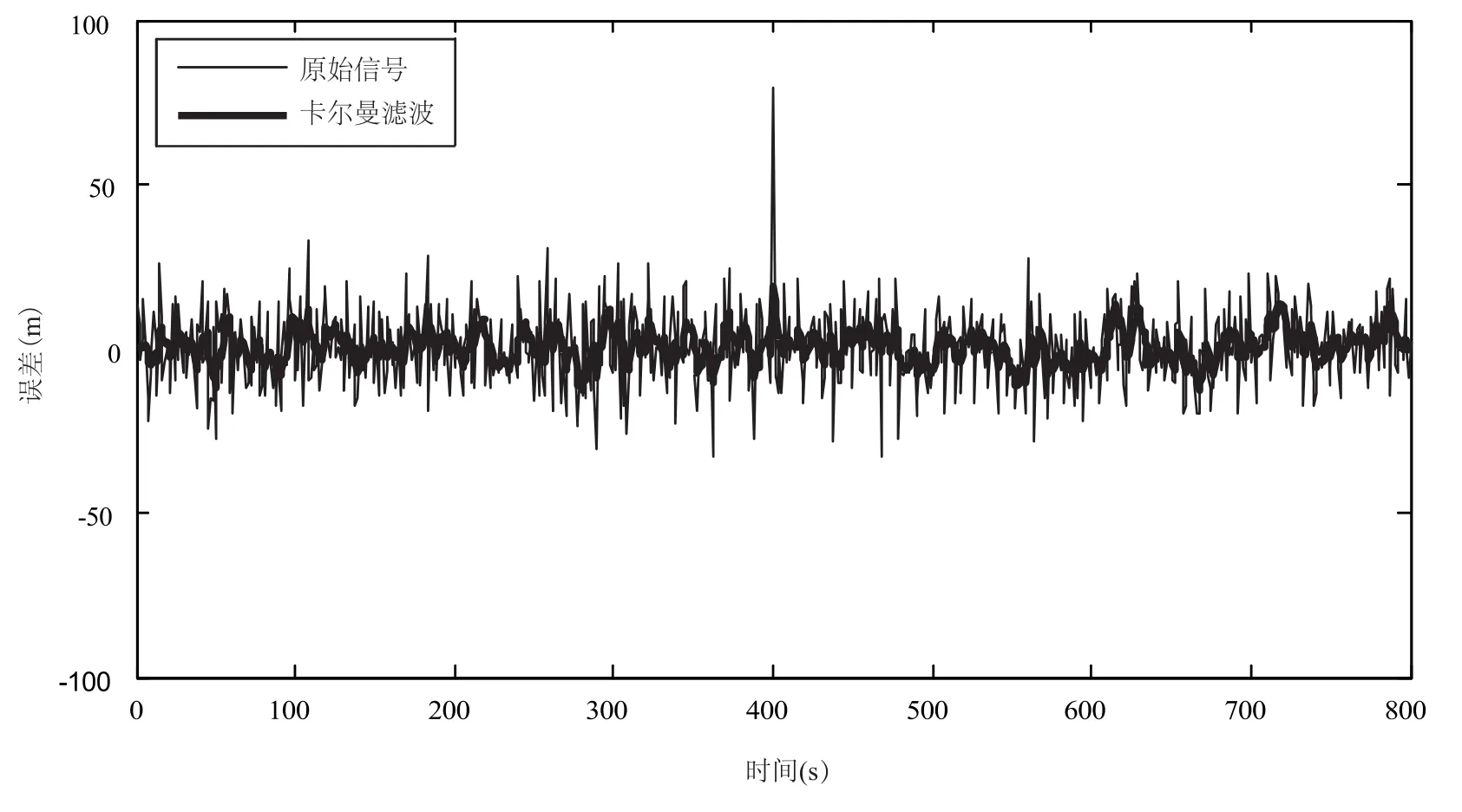
图3 卡尔曼滤波前后车辆GPS导航信号位置误差Fig.3 Positioning error before and after Kalman filtering for vehicle GPS navigation signal
图3是经过卡尔曼滤波前后的车辆GPS导航信号的结果.图4是通过db3小波函数对车辆GPS导航信号进行传统小波变换(5尺度离散小波变换滤波)前后的结果.图5是通过db3提升格式小波函数对车辆GPS导航信号进行5尺度提升小波变换滤波前后的结果.虽然这3种动态滤波算法都能较好地进行车辆GPS导航信号滤波,但传统小波变换、提升小波变换算法滤波性能优于卡尔曼滤波器.为了更精确地对仿真实验结果进行分析与比较,还对图3、图4、图5的数据用式(10)、式(11)、式(12)、式(13)分别进行均方根误差(root mean square error,RMSE)、误差正峰值(error positive peak,EPP)、误差负峰值(error negative peak, ENP)、信噪比(signal to noise ratio,SNR)4个描述误差性能参数的分析计算,其结果如表1所示.
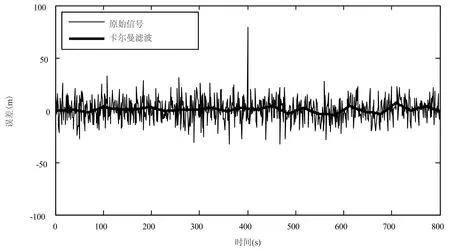
图4 传统小波变换滤波前后车辆GPS导航信号位置误差Fig.4 Positioning error before and after traditional wavelet transformation filtering for vehicle GPS navigation signal
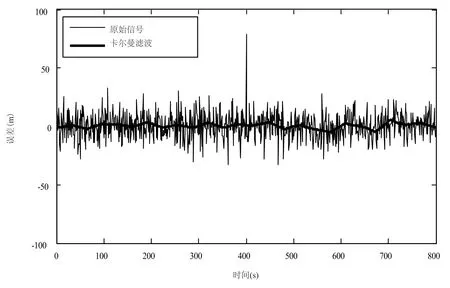
图5 提升小波变换滤波前后车辆GPS导航信号位置误差Fig.5 Positioning error before and after lifting wavelet transformation filtering for vehicle GPS navigation signal
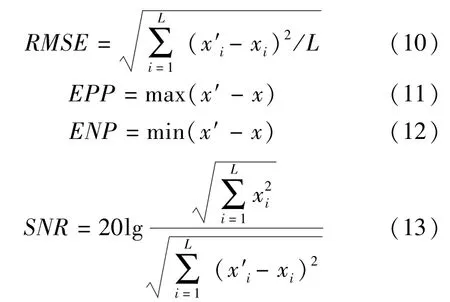
式中 xi、x′i分别为信号的真值和测量值(或数据处理后的值);L为信号的长度[7].
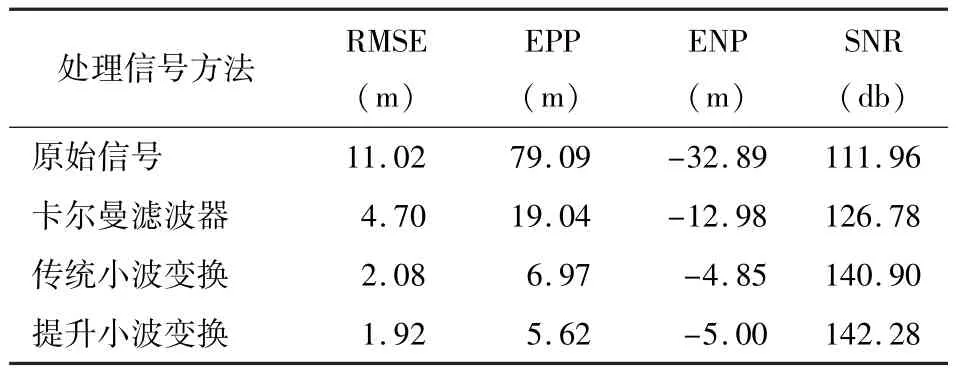
表1 动态滤波后车辆GPS导航信号位置误差比较Table 1 Comparison of vehicle GPS navigation signal position error after dynamic filtering
由表1可知,基于提升小波变换的GPS动态滤波新算法获得了最大的信噪比和最小的均方根误差,取得了最佳的降噪效果和滤波精度,其次分别是传统小波变换和卡尔曼滤波.传统小波变换和提升小波变换算法都能进行粗差探测、剔除数据、数据修复和高精度地动态滤波,但卡尔曼滤波剔除粗差能力较差,最大绝对误差达19.04 m.本文还对这两种小波动态滤波算法进行了计时,提升小波变换动态滤波算法耗时0.062 4 s,传统小波变换动态滤波算法耗时0.124 8 s.这说明虽然提升小波变换动态滤波算法比传统小波变换动态滤波算法的去噪效果(定位精度)稍微高一些;但提升小波变换动态滤波算法的速度比传统小波变换动态滤波算法快一倍,显然对于车辆GPS导航信号的动态滤波处理来讲更为有利.
4 研究结论
本文研究了含有粗差的车辆GPS导航信号的多尺度提升小波变换的特性,提出了车辆GPS导航信号的提升小波变换动态滤波新算法.仿真实验表明,该算法对车辆GPS导航信号进行动态滤波的性能明显优于卡尔曼滤波器,克服了卡尔曼滤波器需建立精确数学模型的不足;虽然在滤波精度方面稍微优于传统小波变换动态滤波算法,但在滤波速度方面比传统小波变换动态滤波算法快1倍.由此可见,在车辆GPS导航系统中对GPS导航信号进行动态滤波处理时采用基于提升小波变换的动态滤波新算法是切实可行的和有效的,这也为车辆GPS导航系统的开发提供了一种可选的新思路.
[1]万德钧,房建成,王庆.GPS动态滤波的理论及其应用[M].南京:江苏科学技术出版社,2000[WAN D J,FANG J C,WANG Q.Theory of GPS dynamic filtering and its application[M].Nanjing:Jiangsu Science and Technology Press,2000.]
[2]毕军,关伟,申金生.车辆GPS/DR定位硬件系统的设计[J].交通运输系统工程与信息,2005,5(3): 24-26.[BI J,GUAN W,SHEN J S.The hardware design of vehicle GPS/DR position system[J].Journal of Transportation Systems Engineering and Information Technology,2005,5(3):24-26.]
[3]李红连,黄丁发.小波变换在车辆GPS导航的应用[J].传感器与微系统,2006,25(7):79-81.[LI H L,HUANG D F.Application of wavelet transformation for vehicle GPS navigation system[J].Transducer and Microsystem Technologies,2006,25(7):79-81.]
[4]Li Hong-lian,Zhang Wei-li,Zhang Jun,et al.A new GPS dynamic filter algorithm based on stationary wavelet transformation [C]. ETP international conference on future computer and communication, 2009:270-272.
[5]熊永良,黄丁发,张献洲.一种基于小波变换GPS基线求解算法[J].测绘学院学报,2000,17(4): 260-264.[XIONG Y L,HUANG D F,ZHANG X Z. A data processing algorithm for GPS base line based on wavelet transform[J].Journal of institute of surveying and mapping,2000,17(4):260-264.]
[6]郭秋英、胡振琪.基于小波变换的GPS快速精密定位[J].煤炭学报,2007,32(11):1179-1182.[GUO Q Y,HU Z Q.GPS rapid precise positioning based on wavelet transform[J].Journal of China Coal Society, 2007,32(11):1179-1182.]
[7]梁高翔,马铁华,张艳兵.基于提升小波变换的容栅传感器输出信号降噪[J].传感技术学报,2011,24 (8):1178-1181.[LIANG G X,MA T H,ZHANG Y B.Denoising of capacitive bars sensor signal based on lifting wavelet transform[J].Chinese Journal ofSensors and Actuators,2011,24(8):1178-1181.]
[8]高永梅,欧吉坤.基于提升小波的GPS周跳探测仿真分析[J].煤炭学报,2009,34(11):1494-1498. [GAO Y M,OU J K.Simulation analysis of GPS cycle-slip detection based on lifting wavelet[J]. Journal of China Coal Society,2009,34(11): 1494-1498.]
[9]何永红,文鸿雁,靳鹏伟.第二代小波在GPS双差观测值消噪中的应用[J].大地测量与地球动力学,2010,30(3):92-95.[HE Y H,WEN H Y,JIN P W.Application based on second-generation wavelet in signal de-noising of GPS double difference observations [J].Journal of Geodesy and Geodynamics,2010,30 (3):92-95.]
[10]赵瑞珍.一种基于小波变换的白噪声消噪方法的改进[D].西安电子科技大学,2001.[ZHAO R Z. Study on wavelet theory and its algorithms for image and signal processing[D].Xidian University,2001]
GPS Dynamic Filter Algorithm Based on Lifting Wavelet Transformation
LI Hong-lian1,2,FANG Hong1,TANG Ju2,ZHANG Jun3
(1.School of Electric and Information Engineering,Chengdu University,Chengdu 610106,China; 2.School of Electronic Engineering,Chongqing University,Chongqing 400044,China; 3.School of Strategical Planning,Chongqing Technology and Business University,Chongqing 400067,China)
It is difficult to establish a precise mathematical model of dynamic filtering for vehicle GPS navigation with Kalman filtering.And the traditional wavelet transformation has some shortness in real-time processing.This paper proposes a GPS dynamic filter algorithm based on the lifting wavelet transformation (LWT).It first decomposes the vehicle GPS navigation signal with the LWT.Then,it detects,eliminates and corrects the signal's gross error at different LWT resolution levels with statistical 3σrule and polynomial interpolation method.The signal's noise is de-noised at different LWT resolution levels with modulus square soft-threshold de-noising method.Finally,the algorithm realizes real-time dynamic filtering for the vehicle GPS navigation system through reconstructing the de-noised LWT coefficients.The simulation results showthat the algorithm is more effective than the Kalman filter in positioning precision.Compared with the traditional wavelet transformation,the speed is doubled for dynamic filtering even though the proposed algorithm only has little advantages on the positioning accuracy.Therefore,the algorithm is available for vehicle GPS navigation system.
intelligent transportation;dynamic filter;lifting wavelet transformation(LWT);vehicle GPS navigation system;3σ rule
U491
A
U491
A
1009-6744(2013)01-0043-06
2012-09-05
2012-09-21录用日期:2012-10-10
国家自然科学基金(11205022);国家社会科学基金(10XGL0013);重庆市自然科学基金(CSTC2008BB0327);四川省科技支撑计划(2012GZX0083);四川省教育厅科技项目(12ZB170).
李红连(1973-),男,重庆忠县人,博士后,副教授.
*通讯作者:cqtangju@vip.sina.com

