基于差异化的航空公司动态价格竞争的复杂性

胡 荣,夏洪山,姜 雨

(南京航空航天大学民航学院,南京210016)

基于差异化的航空公司动态价格竞争的复杂性

胡 荣*,夏洪山,姜 雨

(南京航空航天大学民航学院,南京210016)

为深入分析航空公司动态价格竞争的复杂性,运用非线性动力学的分支理论,构建了基于差异化的航空公司动态价格竞争模型,依据动力学稳定性判定条件,讨论了该模型均衡点的存在性、存在个数与稳定性,数值仿真了不同条件下模型复杂的动力学行为.仿真结果表明,航空公司价格调整速度对模型的稳定性有明显的影响,一旦价格调整速度超过某一临界值,系统将表现出分岔、混沌等复杂的动力学现象;与Nash均衡利润相比,在混沌状态下航空公司的利润均显著下降;差异化战略对航空公司定价、利润有重要影响,保持和加强对竞争对手的差异化优势有助于自身获得更大的市场竞争优势.

航空运输;价格竞争;分支理论;航空公司;复杂性

1 引 言

由于当前国内航空公司对机票代理的严重依赖、对价格管控水平滞后于行业的价格放松机制,以及航权分配缺乏标准规则等因素,使得航空公司迫于竞争压力,常常运用价格手段来打击竞争对手、扩大市场份额,这往往会引发价格战,造成市场竞争秩序混乱,航空公司利益受损[1].国内航空运输市场主要由国航、南航、东航等少数几个航空公司所占据,属于典型的寡头垄断市场.在这种市场结构下,航空公司的定价决策不仅会影响到竞争对手的定价行为,甚至会影响整个市场的结构.因此,航空公司在决定定价策略时,都要考虑到竞争对手对自身企业竞争策略的态度和反应.博弈理论为研究这类问题提供了有效的途径.

近年来,国内外很多学者利用博弈理论研究航空运输市场的定价与经营问题.文献[2]讨论了两个航空公司同时定价与序贯定价的非合作博弈模型;文献[3]构建了期权定价的Stackelberg博弈模型,分析了航空公司的最优定价决策;文献[4]建立了两阶段的运力期权定价模型,研究了航空公司等定价决策;文献[5]研究了不同座位配置规则下的航空公司定价问题;文献[6]分别构建了完全信息和不完全信息的价格竞争博弈模型,分析了航空公司之间恶性价格竞争的缘由;文献[7]运用Hotelling模型研究了航空公司定价问题;文献[8]运用博弈理论研究了政府对航空价格管制的问题.还有很多学者研究了基于收益管理的一般价格策略、实时动态定价、确定型和随机性需求定价、同质产品的动态定价及航空定价联盟等问题[9-11].

纵观国内外航空公司价格竞争的相关文献,当前尚有如下值得进一步研究的内容:一是几乎所有的文献均假设航空公司在价格竞争决策中具有完全理性.但在实际中,航空公司不可能了解足够、完全的市场信息,价格竞争决策只能是有限理性的;二是大多数文献假设航空公司是同质的,提供的产品不存在差异化,但考虑到航线网络、服务质量、营销渠道等因素,几乎没有能提供完全相同产品的航空公司;三是大多数文献仅对航空公司价格竞争模型进行了静态博弈分析,但由于决策的有限理性,这就决定了航空公司之间的价格竞争需要经过重复多次的价格博弈逐步实现市场均衡.

因此,基于上述三点,同时考虑到我国目前的航空需求仍是比较缺乏弹性的[8],本文运用平均价格定价模型,构建基于差异化和有限理性的航空公司动态价格竞争模型,根据非线性动力学理论,分析动态价格竞争模型均衡点的存在性与稳定性,并仿真模拟不同市场参数条件下的航空公司动态行为.

2 基本模型

假定某一航空运输市场中仅有两家航空公司进行重复多次的动态价格竞争,不妨设第i家航空公司在时期 t的机票价格为 pi(t),旅客流量为qi(t),其中i=1,2,t=0,1,2,…,下同.由Dowrick及Raju提出的消费者效用及需求函数,可得出航空运输市场的市场需求函数

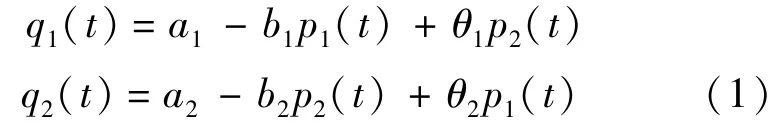
式中 ai表示市场对航空公司i的需求水平,ai＞0(i=1,2);bi表示价格敏感系数,该系数数值越大表明需求的价格弹性越大,bi＞0(i=1,2);θi表示差异化系数,其反映的是航空公司之间的差异化程度,θi＞0(i=1,2).具体而言,差异化系数θ1表示第2家航空公司对第1家航空公司的差异化程度,θ1越小表明两者差异化程度越大,替代性越小;当θ1=0时,表示两者提供的产品完全不相关,此时第2家航空公司对第1家航空公司的差异化程度最大,替代性最小.一般而言,有0＜θi＜bi(i= 1,2),这意味着某航空公司自己的价格影响大于交叉价格的影响.为更清楚考察差异化对航空公司价格竞争的影响且不失一般性,我们令a1=a2,b1=b2, θ1≠θ2,则市场需求函数为

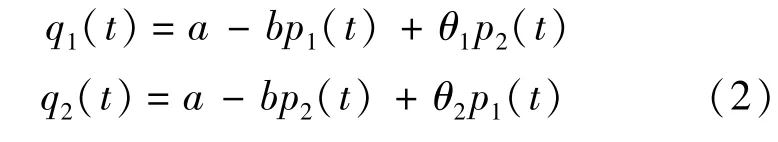
假设两家航空公司的成本函数均为线性形式,即Ci=ciqi.则根据上述条件,航空公司在时期t的利润函数为

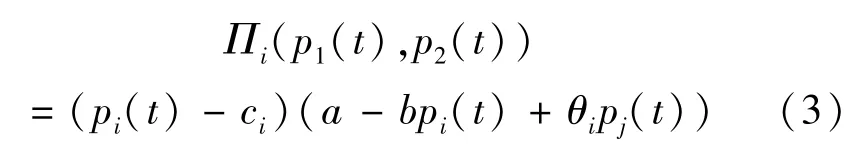
式中 i,j=1,2,i≠j.对于任意给定的时期t,对Πi(p1,p2)关于pi求偏导,可得到第i家航空公司

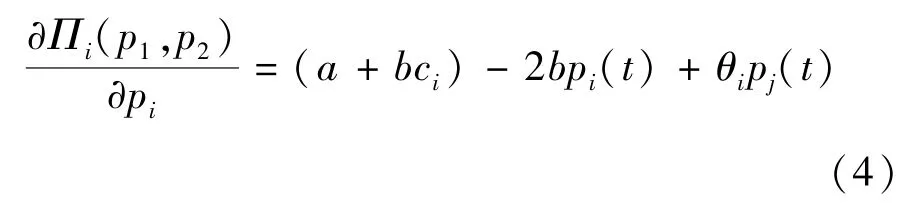
由式(4)可以进一步求得航空公司i面对竞争对手航空公司j的最优价格反应决策为在当期的边际利润为

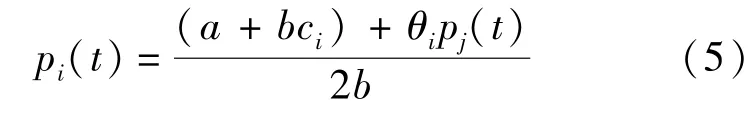
式(5)表示的是航空公司i具有完全理性时的最优价格反应决策.所以式(5)描述的最优反应决策也可称为“完美”决策.

由于航空公司在价格竞争决策中的有限理性,需要不断地对价格进行调整,通过多次的价格竞争最终达到均衡状态.本文假定两家航空公司均采用“短视”调整机制,即航空公司基于上期价格竞争的边际利润情况,对其本期价格决策进行如下的动态调整:在时期t,如果估计的边际利润是正(负)的,那么该航空公司将提高(降低)第t+1期的价格.则有

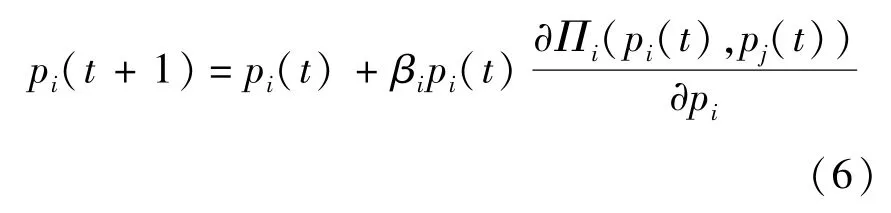
式中 βi表示第i家航空公司的价格调整速度,βi＞0,其反映了该航空公司对边际利润信号的反应速度.

由式(4)、式(6),得到具有差异化和有限理性的航空公司动态价格竞争模型

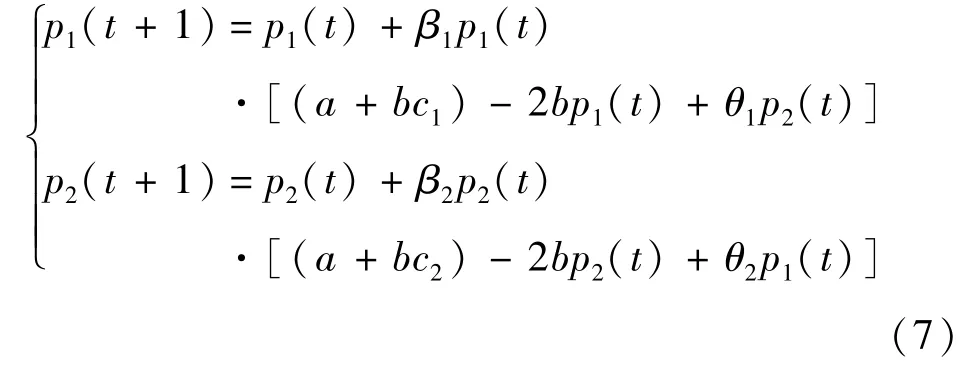
3 模型分析

由于式(7)描述的是航空公司动态价格博弈问题,因此只有当均衡点非负时才有现实意义.故在式(7)中令pi(t+1)= pi(t),可得如下非线性代数

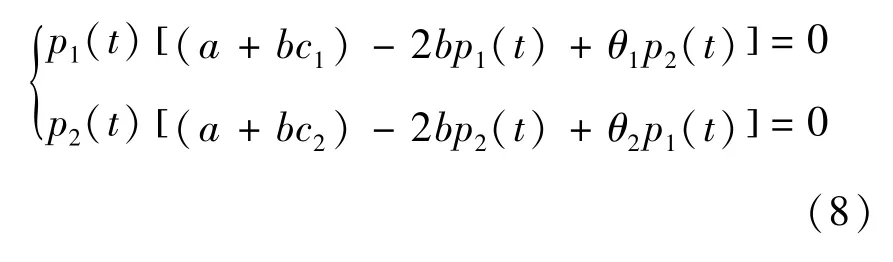
式(8)共有4个均衡点:E0=(0,0),E1=(0,

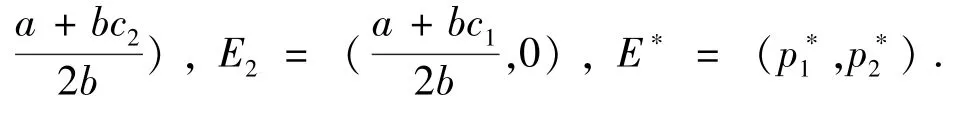
其中

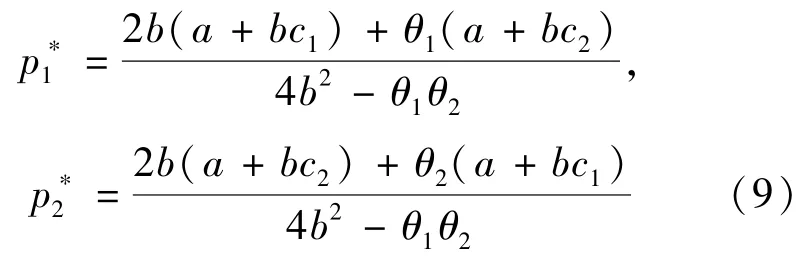
因为0＜θi＜b(i=1,2),则有4b2-θ1θ2＞0,因此p*i＞0.显然,E0,E1,E2为有界均衡点,E*为Nash均衡点.根据动力系统的稳定性判定定理及JULY条件易得如下定理[12,13].

定理1式(7)的有界均衡点E0,E1,E2是不稳定均衡点.

定理2当参数满足4b(β1p*1+β2p*2)-4＜(4b2-θ1θ2)β1β2p*1p*2＜2b(β1p*1+β2p*2)的条件时,Nash均衡点E*是式(7)的稳定点.

由于两家航空公司都是基于有限理性做出价格竞争决策的,因此市场价格不可能立即达到Nash均衡状态,需要进行反复的博弈,最终才能达到平衡.由上文分析可知,一旦某个航空公司,或者两个航空公司的价格调整速度过快,使得β1、β2超出了定理2的条件,则都会导致系统的不稳定.但β1、β2的不同取值不会改变价格的Nash均衡点,即对点E*的取值没有影响.

4 数值仿真

为更好地了解式(7)的动态行为,更清晰地描绘差异化对航空公司价格竞争的影响,本节将对式(7)进行数值仿真.设市场需求函数的参数a=2.65,b=1,航空公司服务单位旅客流量的成本分别为c1=0.6、c2=0.5,航空公司间的差异化系数分别为θ1=0.7、θ2=0.6,第1家航空公司的价格调整速度为β1=0.3,两家公司的初始市场价格为(2,3).

图1描绘的是当系统参数取上述初始值时,两家航空公司价格竞争随第2家航空公司价格调整速度β2变化的动态演化图.从图中可看出,随着β2不断增大,式(7)由初期的均衡状态逐步进入到分岔和混沌状态.当系统陷入分岔和混沌状态后,航空公司间的价格竞争波动很大,很难做出长期预测,给航空公司的价格决策带来困难.

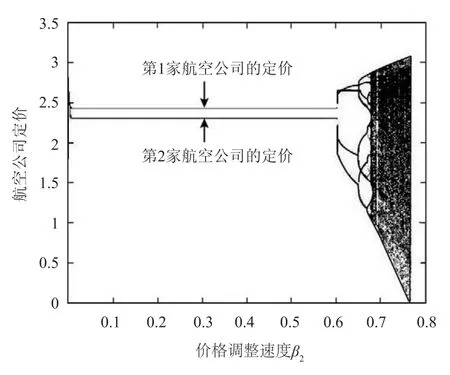
图1 航空公司价格竞争的动态演化图Fig.1 Bifurcation diagram of airlines'price competition

图2描绘的是博弈周期数T=1 000时,式(7)中航空公司平均利润随价格调整速度β2变化的动态演化图.从图中可看出,当系统进入到分岔或混沌状态后,两家航空公司的平均利润均显著低于其在均衡状态下的平均利润.这说明因第2家航空公司而引起的系统波动对两家航空公司均是有害的.为获取最大利润,两家航空公司均有对陷入分岔或混沌状态的系统实施混沌控制的原始动力.

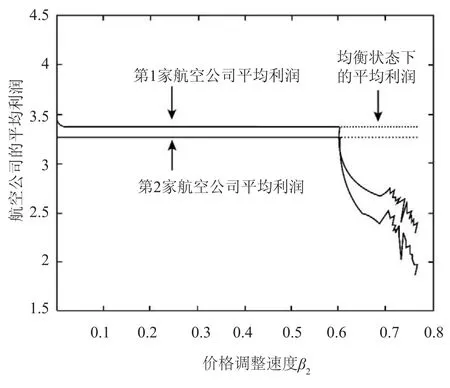
图2 航空公司平均利润的动态演化图Fig.2 Bifurcation diagram of airlines'average profit

图3a、图3b分别描绘了当第2家航空公司价格调整速度β2=0.48,其他系统参数取初始值时,航空公司的价格、利润随差异化系数θ1变化的动态演化图.从图中可以看出,随着差异化系数θ1不断增大,航空公司间的价格竞争由初期的均衡状态最终进入混沌状态.

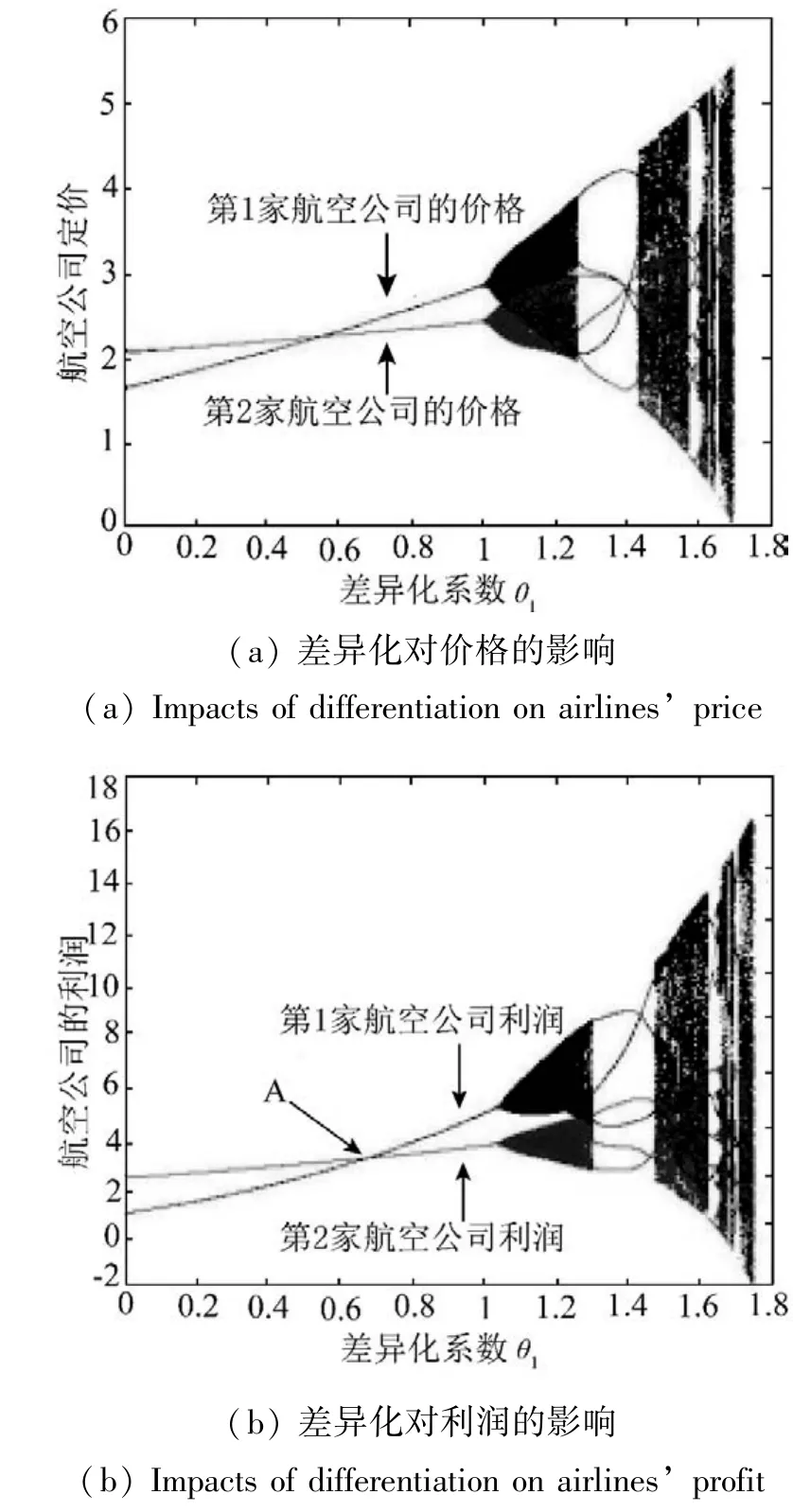
图3 差异化对航空公司的影响演化图Fig.3 Impacts of differentiation on airlines' price and profit

从图3中可以看出,在θ2保持不变的竞争均衡状态下,随着θ1不断增大,第1家航空公司的价格和利润有着快速提高:由θ1较小时价格和利润均低于第2家航空公司,逐渐演变为θ1较大时价格和利润均高于第2家航空公司.这说明第1家航空公司在保持对第2家航空公司的差异化程度不变的基础上(即θ2保持不变),通过降低第2家航空公司的差异化优势,增强对其的替代性(即θ1不断增大),可在市场竞争中更大的收益.

需要特别指出的是,当θ1=0.669 8时,两家航空公司的利润π1=π2=3.214 4,如图3b中点A所示.此时θ1＞θ2=0.6,表明第1家航空公司在保持自身对第2家航空公司的差异化优势的基础上(即θ2保持不变),可以通过削弱第2家航空公司的差异化优势(即θ1不断增大),来弥补其在经营成本上的弱势(c1＞c2),进而增强其在市场竞争中的整体优势.

奇异吸引子是混沌运动的主要特征之一,它体现了系统进入混沌状态后复杂现象的内在规律性表现.因此,当系统进入混沌状态时,航空公司可以根据吸引子表现出来的规律性来对短期的价格竞争进行预测.图4给出了系统参数取图1值情形下的奇异吸引子.同时,通过数值仿真发现,在其他系统参数不变的条件下,选取大于临界值(β1*或β*)的价格调整速度,对应的奇异吸引子会有所不2同,但都反应了系统进入混沌状态后航空公司动态价格竞争的复杂性.

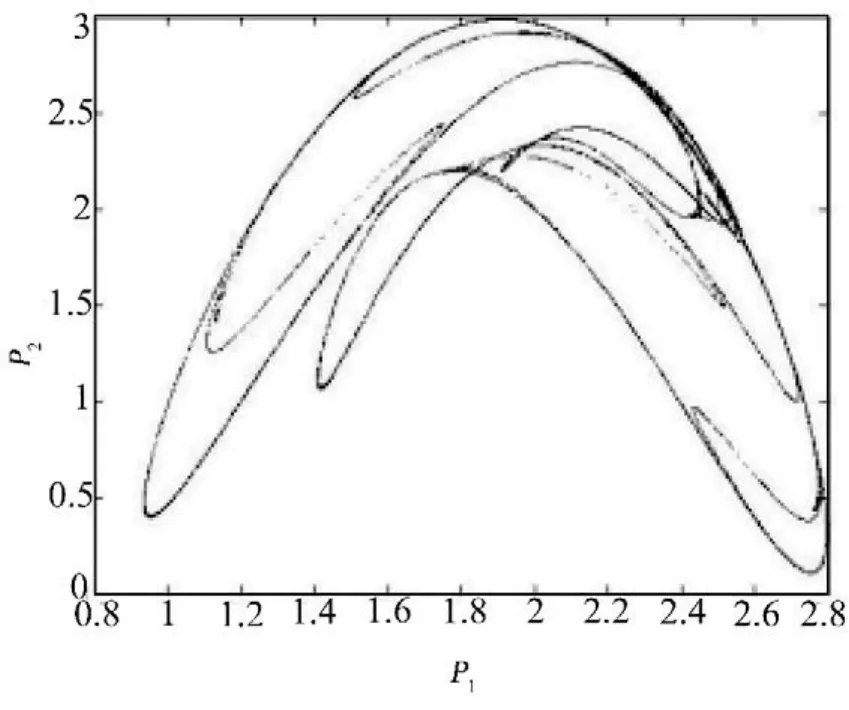
图4 航空公司动态价格竞争系统的奇异吸引子Fig.4 Strange attractor for a=0.3

对初始条件的敏感依赖性也是系统混沌行为的特征之一.为验证有限理性航空公司动态价格竞争模型是否对初始条件具有敏感依赖性,设第2家航空公司价格调整速度β2=0.75(由图1可知,此时系统处于混沌状态),其他参数取初始值.图5a、图5b分别描绘了航空公司初始价格分别为(2,3)和(2.000 1,3)时,第1家航空公司价格随时间t的变化历程.对比图5a、图5b可以看出,在初始阶段.两个价格时间序列基本是无差别的,但经过一段博弈周期后,两个序列的取值出现了巨大的差异.由此看出,即使初始价格微小的变动都会对最终价格竞争结果产生非常大的影响.同理也可发现第2家航空公司价格变化也具有同样的敏感依赖性.这也证明了航空公司动态价格博弈式(7)中存在着复杂的动力学行为.

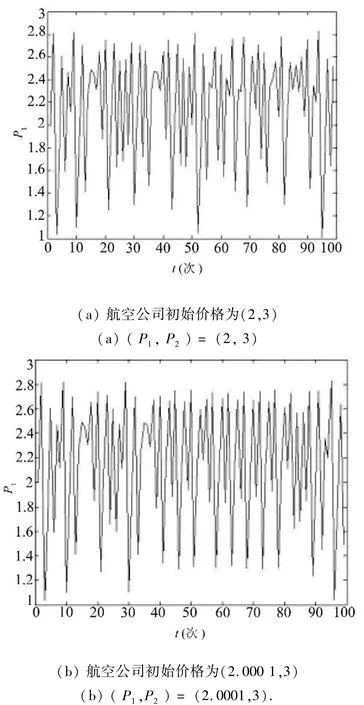
图5 第1家航空公司价格对初始条件的敏感依赖性Fig.5 Shows sensitive dependence on initial conditions

5 研究结论

本文研究了具有差异化的航空公司动态价格竞争模型,运用非线性动力学理论,分析了模型均衡点的存在性与稳定性,并对模型进行了数值仿真,研究了动态价格竞争模型的复杂性.

文章研究结果表明,具有有限理性的航空公司开展动态价格竞争时,其价格调整速度的快慢对竞争模型的稳定性有显著影响,一旦价格调整速度超过某一临界值,系统将表现出分岔、混沌等复杂的动力学现象;进入分岔和混沌状态后,系统波动将对航空公司均会有不利影响,造成利润的显著下降;差异化对航空公司的定价、利润会产生显著影响,航空公司一方面要尽量保持并加强对竞争对手的差异化优势.另一方面想方设法削弱竞争对手对自己的差异化优势,在对手具有差异化优势的方面加以改进与提升,增大对竞争对手的替代性;通过对混沌吸引子和敏感依赖性的分析,证明航空公司动态价格博弈模型存在着复杂的动力学行为.本文研究结果对航空公司的市场价格竞争决策可提供一些理论参考.

最后,在本文研究基础上,考虑更多寡头公司、不同价格调整机制、不同战略定位等因素的竞争情形,以及对陷入混沌状态的市场进行有效控制等可开展进一步的研究.

[1]Serguei Netssine,Robert A Shumsky.Revenue management games: Horizontal and vertical competition[J].Management Science,2005,51(5): 813-831.

[2]牟德一,李琴.单航线双寡头下的航空公司定价决策[J].管理科学文摘,2008,(4):155-156.[MOU D Y,LI Q.Study on airlines price decision of single line [J].Digest of Management Science,2008,(4): 155-156.]

[3]雷丽彩,周晶.风险规避下的航空货运期权定价Stackelberg博弈模型[J].系统工程理论与实践, 2010,30(2):264-271.[LEI L C,ZHOU J.Stackelberg game model of capacity options for air cargo under risk aversion[J].Systems Engineering-Theory&Practice, 2010,30(2):264-271.]

[4]Rolf H.Capacity options for revenue managementtheory and applications in the air cargo industry[D]. WHU Otto Beisheim School of Management,2006.

[5]许洪,胡运权,李军.航空公司定价动态模型与座位配置研究[J].系统工程理论与实践,2004,24(6): 44-48.[XU H,HU Y Q,LI J.Study on airline pricing and seat allocation[J].Systems Engineering-Theory& Practice,2004,24(6):44-48.]

[6]王锐兰.航空公司价格竞争的博弈解释[J].技术经济与管理研究,2004(3):81-82.[WANG R L.Game theory analysis ofairline price competition [J]. Technoeconomics&Management Research,2004(3): 81-82.]

[7]肖艳颖.航空公司市场竞争定价博弈模型[J].中国民航大学学报,2008,26(6):52-55.[XIAO Y Y. Game theory model of dual oligopoly airlines competition pricing[J].Journal of Civil Aviation University of China,2008,26(6):52-55.]

[8]景崇毅,孙宏,曾文水.机票价格管制问题的博弈分析及解释[J].中国软科学,2008(3):140-147. [JING C Y,SUN H,ZENG W S.Game theory analysis and explanation of air ticket price control problem[J].China Soft Science,2008(3):140-147.]

[9]Lin K Y.Dynamic pricing with real-time demand learning[J].European Journal of Operational Research,2005,30(3):1-17.

[10]Dai Yue,Chao Xiuli,Fang S C,et al.Pricing in revenue management for multiple firms competing for customers[J].International Journal of Production Economics,2005,98(1):1-16.

[11]Zhang Ji xiang,Da Qing li,Wang yan hua.The dynamics of Bertrand model with bounded rationality [J].Chaos,Solitons& Fractals,2009,39(5): 2048-2055.

[12]Agiza H N,Elsadany A A.Nonlinear dynamics in the Cournot duopoly game with heterogeneous players[J]. Physica A,2003,320(15):512-524.

[13]胡荣,陈圻,王强.不同理性双寡头R&D竞争分析与混沌控制[J].控制与决策,2010,25(10):1536-1542.[HU R,CHEN Q,WANG Q.Competition analysis and chaos control of R&D in duopoly with heterogeneous rationality[J].Control and Decision, 2010,25(10):1536-1542.]

Complex Dynamics for Airlines'Price Competition with Differentiation Strategy

HU Rong,XIA Hong-shan,JIANG Yu
(College of Civil Aviation,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China)

To investigate the complex dynamics for airlines'price competition,this paper proposes a price competition model of airlines with differentiation strategy and with the theory of bifurcation of dynamical systems.The existence and stability of equilibrium points of the model are discussed according to dynamic stability criteria.The complex dynamics of this model in different market parameters are shown though numerical simulation.The simulation results show that the speed of price adjustment has a significant impact on the stability of the model,while the speed of price adjustment is larger than critical value,and the phenomenon of bifurcation and chaos will appear on the dynamic system.Compared with the Nash equilibrium profits,all airlines'profits are decreased obviously when chaos is occurred.Differentiation has an important impact on airlines'price and profits,it's helpful to have more competition advantage that to keep and strengthen the differentiation advantage against the competitors.

air transportation;price competition;theory of bifurcation;airlines;complex dynamics

U8;N94

A

U8;N94

A

1009-6744(2013)01-00011-08

2012-09-25

2012-11-08录用日期:2012-11-20

国家自然科学基金(71201082,71101071);中国博士后科学基金项目(2011M500920);江苏省高校哲学社会科学基金项目(2012SJD630083);中央高校基本科研业务费专项资金(NR2012029).

胡荣(1980-),男,江苏扬州人,讲师,博士.

*通讯作者:hoorong@nuaa.edu.cn