实时换乘信息提示下基于乘客偏好的线路选择
胡 萍,马祖军
(西南交通大学经济管理学院,成都 610031)
1 引 言
当乘客面对多条均可到达目的地的线路时,该如何选择?是乘坐已经到站的车辆,还是等待稍后到达但乘车时间更短的车辆.相信在日常生活中,不论是在综合客运枢纽内,还是在普通的公交站台上,乘客都会遇到这样的问题.在没有车辆到站信息提示的情况下,等车时间成了乘客进行线路选择决策的重要影响因素.此时,乘客最快到达目的地的方法就是从所有能到达目的地的线路中选出“吸引线路集”,并乘坐这些线路集合中第一辆到达本站的车辆离开.
随着先进的出行者信息系统(ATIS)的出现及广泛应用,ATIS对乘客的线路选择行为产生了重要影响[1-4].ATIS可以实时、准确、高效地为乘客就出行方式、换乘方式、线路及车次选择等提供咨询,如上海虹桥综合客运枢纽通过分布在枢纽内各处的76块显示屏,可以向乘客实时提供枢纽内各种交通方式的计划班次、实时运行状态、换乘线路以及市区路况等相关信息.在以先进信息系统为支撑的综合客运枢纽内,研究实时换乘信息提示下乘客的线路选择行为,有助于交通管理部门了解乘客的出行规律,从而更好地规划和管理运输系统,提高运输效率.
实时提示信息能够减少乘客直觉上的等车时间[2-3],能够有效调节乘客的线路选择行为[4-6].另外,Hickman和Wilson[7]总结了三条影响实时提示信息使用价值的因素,即车辆行驶时间具有时变特性;由于交通网络处于不确定动态环境中,车辆行驶时间还具有随机性;后续换乘线路中车辆衔接的不确定性,以及由此导致的在本车站选择线路及车辆存在不确定性.然而,信息对乘客出行行为的影响不仅与信息准确程度有关,而且与乘客本身的行为习惯有关.例如,当乘客习惯于某种出行模式时,提示信息对其出行模式选择行为的影响较小[8,9].从心理学角度来讲,习惯是指对某种特定条件形成自动化反应的一系列固定下来的行为方式[10],而偏好则是按照自己的意愿对可供选择的事物或事物组合进行的排序.但目前鲜有基于乘客个体偏好研究实时信息条件下线路选择行为的文献.Gao和Wang[11]从认知学的角度探讨了诱导信息可信度、线路固有偏好以及出行经验等对驾驶员线路选择行为的影响,但研究的是驾驶员线路选择行为,而非乘客线路选择行为,且文中也仅考虑了乘车时间这一负效用.
鉴于此,本文拟探讨乘客在实时换乘信息提示下,结合自身偏好进行线路选择的行为,即探讨乘客对线路存在偏好时,实时提示信息对其线路选择行为的影响.通过估计每条线路的等车时间和乘车时间来计算其负效用,并据此对乘客的线路初始偏好值进行修正.由于实时提示信息不完全准确,将结合时变信息建立基于实时一时变结合策略的期望等车时间的更新机制,在此基础上建立能综合反映实时提示信息和乘客个体偏好对线路选择行为影响的线路选择概率模型.最后,通过数值仿真验证该模型的可行性和有效性,并分析等车时间和乘车时间的权重对乘客线路选择行为的影响.
2 模型建立
2.1 问题描述
乘客在综合客运枢纽内面对多条均可到达目的地的交通线路,希望选择一条总的旅行时间最短的线路.在实际生活中,受出行目的、行为习惯和以往经验等因素的影响,乘客对不同线路有着不同的初始偏好.但根据枢纽内实时提示信息,会进行每条线路总的旅行时间估计,据此对线路初始偏好值进行修正.
本文作如下假设:
(1)乘客可以根据综合客运枢纽内的实时提示信息获悉各线路的等车时间信息.
(2)仅考虑线路总的旅行时间这一负效用,且不考虑乘客上下车所耗时间.
(3)乘客在实时信息提示下,根据每条线路的负效用修正其初始偏好值,并选择修正后偏好值最大的线路.
2.2 线路选择概率模型
假设乘客考虑的吸引线路集由编号为1,2,…,n的若干条备选线路组成,即Rn={1,2,…,n}.设i∈Rn,q0i为乘客对线路i的初始偏好值,表示在没有实时信息提示的情况下乘客对线路i的偏爱程度[11];Δqi为乘客获悉实时提示信息后对线路i初始偏好值的修正量;πi为乘客选择线路i的概率.记Ci为线路i的负效用;ΔCi为线路i与其它线路相比的负效用差值的代数和.乘客在获悉实时提示信息后,对各线路的负效用进行比较,得到ΔCi,再转化为对各线路初始偏好值的修正量Δqi,则线路选择概率模型可表示为
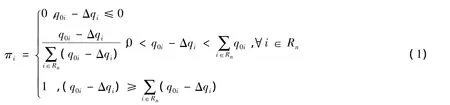
由式(1)可知,乘客选择线路i的概率等价于线路i修正后的偏好值在所有备选线路修正后的偏好值之和中所占的比重.由于要保证乘客选择线路i的概率0≤πi≤1,因此,当乘客对线路i的初始偏好值经修正后为负值或0时,πi取0;当其与所有备选线路修正后偏好值之和的比例大于等于1时,πi取1.
根据假设(3),乘客在实时信息提示下,根据每条线路的负效用对其初始偏好值进行修正.为了能够在同一量纲下完成修正,首先需要将负效用转化为与初始偏好值具有相同量纲的修正量.修正量Δqi计算如下:
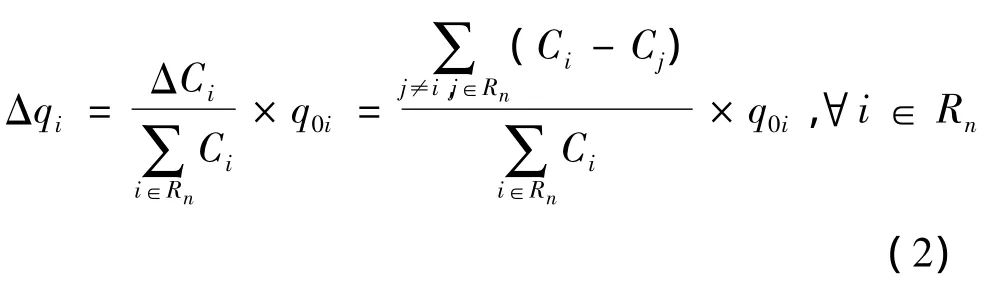
线路i的负效用为期望等车时间E(wi)和乘车时间xi的加权和,即
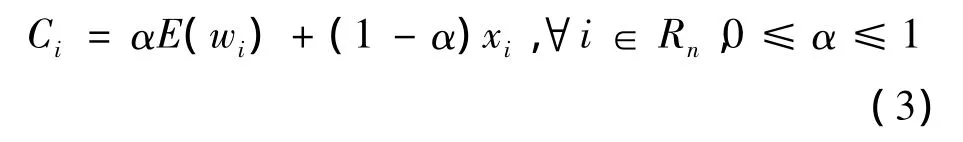
式中 α为权重系数,取值越大表明乘客对等车时间越关注,反之则对乘车时间越重视;E(wi)为实时信息提示下,运用等车时间更新机制更新后的期望等车时间.
2.3 期望等车时间估计
车辆在行驶过程中受交通流量、交通事故、交通管制、天气变化等经常性或偶然性因素的影响,会导致每天和同一天内的不同时段配送车辆在各路段上的行驶时间有所差异.这些因素中有些具有时变或时间依赖性,在一定程度上可以通过对大量日常交通数据的统计分析进行估计,而另一些因素则事先难以预测,只能根据时间的推移实时地获取有关信息.这些实时和时变因素对线路选择决策有重要影响,但以往有关实时信息提示下线路选择的研究中,缺乏考虑车辆行驶的时变特性以及实时提示信息的不完全准确性.为此,本文综合考虑这两类因素,建立了考虑时变信息的实时等车时间更新机制与计算模型.显然,等车时间可通过即将到站的车辆到站时间来反映.
(1)车辆实时到站时间.
实时提示信息可以反映即将到站的车辆当前所处路段的路况及行驶状况.由于道路交通总是处于不确定动态环境中,因而枢纽内发布的车辆到站时间会有一定的误差,可用期望值及其误差分布的形式来表示[7].显然,车辆距离本站越近时,对该车辆到站时间的估计越准确,因而可用区间数[7]描述该信息的误差分布(如表1所示),据此对实时提示信息提供的到站时间进行更新.例如,当信息提示某条线路上的车辆还有5分钟到达本站时,根据实时提示信息的误差分布,可知该车辆还有约4~6.5分钟到站,此时该信息提示的到站时间就由不准确的5分钟转化为4~6.5分钟的准确范围.

表1 车辆实时到站时间准确程度分布Table 1 The accuracy of real-time arrival time
(2)车辆时变到站时间.
根据大量的历史交通数据统计分析可得出每天各个时段(以分钟为单位,如目前北京ITS的实时信息发布系统每2分钟刷新一次)内各路段中车辆的到站时间.在此采用下限为a,上限为b,众数为c的三角分布(a,b,c)来描述车辆时变到站时间.例如,某时段内某条线路上的车辆的时变到站时间分布为(3.0,5.8,4.5),表示该车辆到达本站最晚还有5.8分钟,最早3.0分钟,而概率最大的是4.5分钟.
(3)基于实时一时变结合策略的期望等车时间更新机制.
对于线路i,参照文献[7]设计实时一时变信息相结合的期望等车时间更新机制如下:
Step1根据当前时段得到车辆时变到站时间三角分布(ai1,bi1,ci1),据此得到时变到站时间的期望值adi=(ai1+bi1+ci1)/3.
Step2根据枢纽内发布的车辆实时到站时间Di,由表1中查到相应的误差分布区间[Ai,Bi],则车辆实时到站时间可转化为区间数(a'i2,b'i2),其中a'
i2=Di+Ai,b'i2=Di+Bi.Step3 最可能的车辆到站时间与时变到站时间和信息提示下的实时到站时间都有关,可表示为c'i2=adi+vi,其中vi是从误差分布区间[Ai,Bi]中随机产生的一个实数,表征车辆到站的随机性.
①当a'i2≤c'i2≤b'i2时,表明车辆行驶正常,计算期望到站时间时应考虑时变值,此时车辆到站时间可表示为三角分布(a'i2,b'i2,c'i2),转Step4;
②当c'i2<a'i2或c'i2>b'i2时,表明车辆行驶异常通畅或遇到严重交通堵塞,计算期望到站时间时不宜考虑时变值.此时车辆到站时间即为区间数(a'i2,b'i2),则车辆期望到站时间(即期望等车时间)E(wi)=(a'i2+b'i2)/2,转 Step6.
Step4由于车辆在正常运行情况下到站时间的最大值、最小值和最可能值不应超过时变到站时间范围,因而还需要对a'i2,b'i2和c'i2的值进行修订,即ai2=max(ai1,a'i2),bi2=min(bi1,b'i2),ci2=min(max(ai1,c'i2),bi1).
Step5至此可计算实时信息提示下的车辆期望到站时间(即期望等车时间)E(wi)=(ai2+bi2+ci2)/3.
Step6输出E(wi).
3 数值仿真
假设某时刻乘客进入综合客运枢纽后,有2条均可到达目的地的线路Ⅰ和Ⅱ.设乘客到达客运枢纽内车站的时刻为t,对应时段为τ,设每4分钟为一时段.本文不考虑跨时段情况,为了方便描述,令t=0,即将乘客到站的时刻记为0时刻,从0时刻对应的第τ时段内的到站时间开始算起,两条线路的时变到站时间分布如表2所示;实时到站时间的信息提示每1分钟更新一次,具体数值如表3所示,信息准确度(误差)的分布如表1所示.乘客对两条线路的初始偏好分别为q0Ⅰ=4和q0Ⅱ=6,且α=0.5.假设两条线路Ⅰ和Ⅱ的乘车时间分别为32.71 min和46.56 min.求乘客选择两条线路的概率.
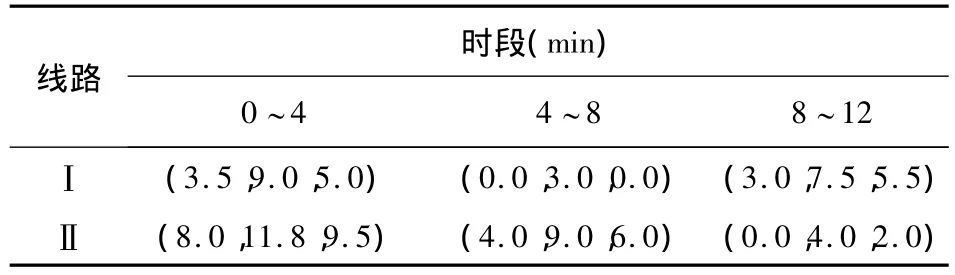
表2 车辆时变到站时间Table 2 Time-dependent arrival time

表3 车辆实时到站时间提示Table 3 Guidance about real-time arrival time
3.1 结果分析
由题示信息,可根据上文提出的期望等车时间更新机制求得乘客在各时段内的期望等车时间如表4所示.
当α=0.5,即等车时间和乘车时间对乘客线路选择行为的影响程度相同时,根据式(3)可求得乘客选择线路Ⅰ和Ⅱ的负效用如表5所示.

表4 期望等车时间Table 4 Expected waiting time

表5 线路Ⅰ和Ⅱ的负效用Table 5 The disutility of routeⅠandⅡ
图1给出了乘客对两条线路分别具有不同初始偏好条件下的线路选择概率图.图中横坐标代表等车时间,纵坐标代表线路选择概率,折线代表不同时段内乘客选择线路概率的变化情况.
对照图1和表5可以看出:在0~3分钟这3个时段内,由于乘客对线路Ⅱ的初始偏好较大,虽然线路Ⅰ的负效用比线路Ⅱ小,但这一优势不足以抵消乘客对线路Ⅱ的原始偏好,故乘客仍会坚持选择线路Ⅱ;从第3分钟开始至第8分钟结束的几个时段内,线路I的优势超过了乘客对线路Ⅱ的初始偏好,故乘客选择线路Ⅰ的概率越来越大.可见,实时提示信息引起了乘客对各线路的初始偏好值的修正.
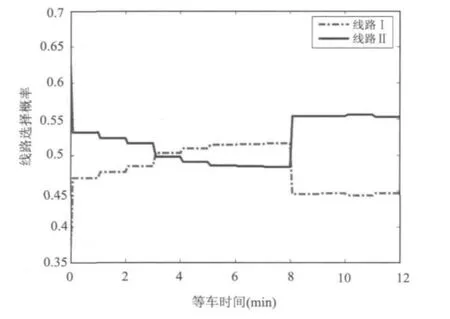
图1 具有不同初始偏好时线路选择概率图Fig.1 Route choice probabilityfor different initial preference
由于第8分钟开始前线路Ⅰ的头一辆车已经到站,因而之后的几个时段内实时提示信息对线路Ⅰ的提示是下一辆车的到站时间.对照表4、表5和图1不难看出,此后几个时段内线路Ⅱ的乘车时间较长是导致其负效用较大的主要原因.线路Ⅱ的乘车时间虽然较长,但由于乘客对其具有较大的初始偏好,且这一优势足以弥补乘车时间较长的缺憾,故此后几个时段内乘客将选择线路Ⅱ.
上述分析表明:首先,乘客的个体偏好会对其线路选择行为产生重要影响;其次,乘客选择线路时不是单纯地考虑等车时间或乘车时间最短,而是结合实时提示信息综合考虑线路的负效用最小;第三,当某线路的负效用优势足以弥补其初始偏好不足时,初始偏好将被修正,继而改变乘客的线路选择行为.
3.2 权重的影响分析
权重α与1-α分别表示等车时间和乘车时间对乘客线路选择行为的影响程度.当乘客只重视乘车时间或等车时间的情况下,即α分别取0和1时,上述算例的仿真结果如图2所示.
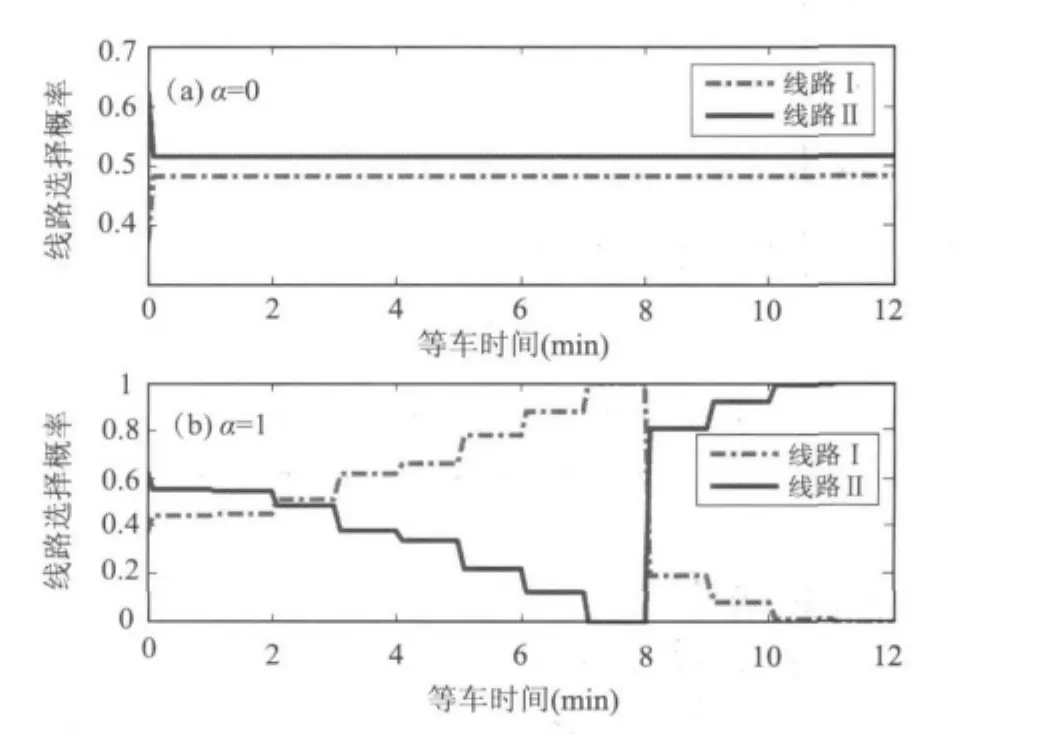
图2 α=0和α=1时的线路选择概率图Fig.2 Route choice probability for α =0 and α =1
可以看出,当α=0,即乘客只考虑乘车时间时,由于线路Ⅱ的乘车时间较短,乘客将始终选择线路Ⅱ.对比图1和图2可以发现,随着α的增大,前8分钟内(至线路Ⅰ的头一辆车到站为止),乘客选择线路Ⅰ的概率越来越大,其主要原因在于线路Ⅰ的等车时间本来较短,加上其权重又逐渐增大,综合乘车时间后的优势已经越来越大于线路Ⅱ的初始偏好;在8~12分钟内,乘客只会选择线路Ⅱ,且该时段内选择线路II的概率不断增大,其主要原因在于线路Ⅰ等车时间较长的情况下,虽然其乘车时间较短,但随着α的逐渐增大,等车时间对乘客线路选择行为的影响程度增大,故综合后的优势越来越弱.
根据仿真图的变化趋势可以判定,上述算例在α=0~0.5间必然存在一个 α的临界值,使得πⅠ≤πⅡ.通过仿真发现,当 α≤0.3时,满足πⅠ≤πⅡ,α=0.3时的仿真结果如图3所示.故α=0.3为前8分钟内是否选择线路I的临界值.
可见,α的取值对乘客线路选择行为有重要影响.了解乘客线路选择行为随α的变化情况,有利于交通管理部门掌握乘客的行为规律,从而制定有效措施(如合理调整各线路的发车频率)来实现客流的合理分配.
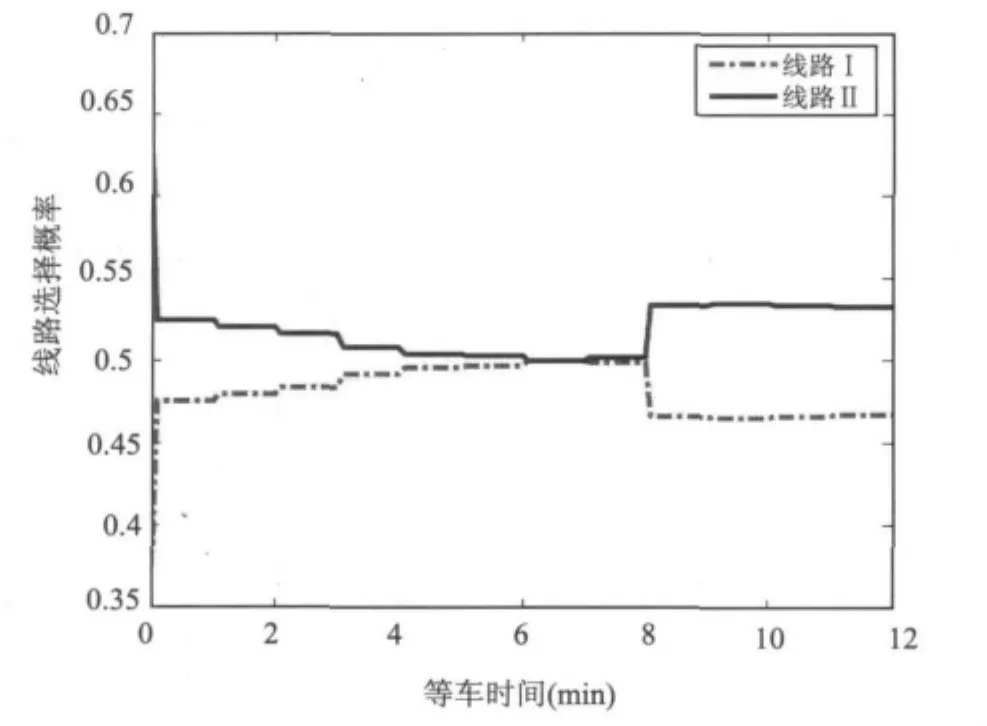
图3 α=0.3时的线路选择概率图Fig.3 Route choice probability for α =0.3
4 研究结论
本文根据综合客运枢纽发布的实时换乘提示信息,结合乘客的个体偏好对其线路选择行为进行了研究.在综合考虑实时提示信息、线路负效用及乘客个体偏好这三方面因素的基础上,建立了线路选择概率模型.依据乘客期望总的旅行时间最短这一原则,提出了线路初始偏好值修正量的计算方法,并设计了实时提示信息不完全准确情况下期望等车时间的更新机制.最后,通过数值仿真验证了该模型的可行性和有效性,并分析了等车时间和乘车时间的权重对乘客线路选择行为的影响.结果表明:首先,实时提示信息和乘客个体偏好都会对乘客的线路选择行为产生重要影响;其次,实时提示信息会通过修正乘客对各线路的初始偏好继而改变乘客的线路选择行为,但只有当某线路的负效用优势足以弥补其初始偏好不足时,才会改变乘客的线路选择行为;最后,乘客对等车时间和乘车时间的关注程度也会影响其线路选择行为.
本文虽然以单个乘客为研究对象,但群体乘客的行为正是诸多个体行为的综合体现,因而可以通过对一定数量具有不同特征的个体乘客行为的研究,间接地反映群体乘客的行为规律.此外,本文所提研究方法具有一定的普适性,例如可以扩展用于出行方式选择研究.当然,由于乘客出行行为的复杂性,还有许多问题值得进一步探讨.例如在实际生活中,除了乘客个体偏好会对其线路选择产生影响外,价格优惠、线路舒适度等也是选择行为研究中不容忽视的因素.因此,深入研究基于乘客个体偏好的线路选择行为,有利于交通管理部门更好地掌握乘客的出行行为规律,以便更好地规划设计公交系统,帮助乘客实现更为方便有效的出行.
[1]Shimamoto H,Kurauchi F,Iida Y.Evaluation of effect of arrival time information provision using transit assignment model[J].International Journal of ITS Research,2005,3(1):11-18.
[2]Dziekan K,Vermeulen A J.Psychologicale effects and design preferences for real-time information displays[J].Journal of Public Transportation,2006,9(1):71-89.
[3]Dziekan K,Kottenhoff K.Dynamic at-stop real-time information displays for public transport:effects on customers[J].Transportation Research Part A:Policy and Practice,2007,41(6):489-501.
[4]Larsen O I,Sunde O.Waiting time and the role and the value of information in scheduled transport[J].Research in Transportation Economics,2008,23(1):41-52.
[5]Chorus C G,Arentze T A,Molin E J E,et al.The value of travel information:Decision strategy-specific conceptualization and numerical examples[J].Transportation Research PartB:Methodological,2006,40(6):504-519.
[6]Gentile G,NguyenS,Pallottino S.Route choice on transit networks with online information at stops[J].Transportation Science,2005,39(3):289-297.
[7]Hickman M D,Wilson N H M.Passenger travel time and path choice implicationsofreal-time transit information[J].Transportation Research Part C:Emerging Technologies,1995,3(4):211-226.
[8]Kenyon S,Lyons G.The value of integrated multimodal traveler information and its potential contribution to modal change[J].Transportation Research Part F:Traffic Psychology and Behaviour,2003,6(1):1-21.
[9]Walker M.The factors affecting the acquisition of bus passenger information in stable and unstable environments[D].PhD thesis,University of Wales,Cardiff,1998.
[10]Aarts H,Verplanken B,Van Knippenberg A.Habit and information use in travel choices[J].Acta Psychologica,1997,96(1-2):1-14.
[11]Gao F,Wang M Z.Route choice behavior model with guidance information[J].Journal of Transportation SystemsEngineering and Information Technology,2010,10(6):64-69.

