不确定Sigma－Delta调制器的鲁棒滤波

王英俊，王武，王骞

(福州大学电气工程与自动化学院，福建福州 350116)

0 引言

随着数字信号处理器(digital signal processor，DSP)在工业和生活中的广泛应用，引发了对高效率、高速、高精度模数转换器的强烈需求.传统的ADC以奈奎斯特速率进行直接采样，无法达到很高的精度.而Sigma－Delta调制器(Sigma－Delta modulator，SDM)引入过采样和反馈技术，使其具有高精度、高线性、便于与数字系统集成等优点［1］.

为了提高SDM性能，目前普遍采用的结构有单回路高阶、级联结构以及多位调制器结构［2］.级联调制器结构能在低采样率下实现高阶噪声整型同时能很好避免电路不稳定现象.然而由于存在电路补偿部分，这种结构对电路的非理想性比较敏感.因此级联结构中电路结构不确定性的补偿和校正成为了近年来研究的热点.至目前为止对SDM的不确定性问题描述仍然局限于采用凸多面体或转化为连续域的形式进行描述［3］，采用更加直接的描述方法研究设计滤波器未见有文献报道.

本研究基于线性区间系统的方法设计鲁棒控制器.利用MARKOV区间算法将级联SDM的参数不确定性问题描述为在一个区间范围内波动但波动幅值已知的区间矩阵，其等效描述形式类似于范数有界摄动形式.针对这一类区间系统，运用LMI方法给出鲁棒H∞控制器存在的充分条件.最后通过实际数字仿真说明了滤波器的设计过程及其有效性.

1 问题描述

考虑三阶级联2－1结构的SDM［4］，如图1所示，其中Hi(z)(i=1，2，3)为积分模块，P(z)和Q(z)为数字校正滤波器.第一级的输出信号可表示为:

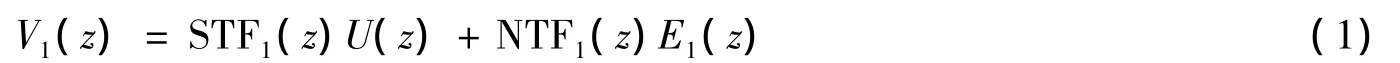
其中:STF1和NTF1为第一级的信号传递函数和噪声传递函数，可表示为:

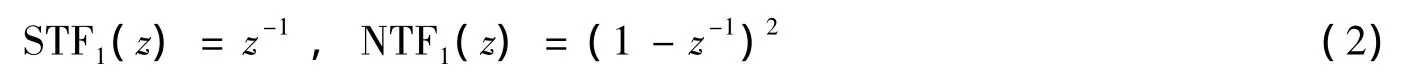
第二级回路可大大增加系统的信噪比，图1中第一级输出与内部量化器信号相减可得到量化器噪声E1的模拟信号形式，将E1输入到另一个SDM回路中形成第二级结构.第二级输出信号可表示为:

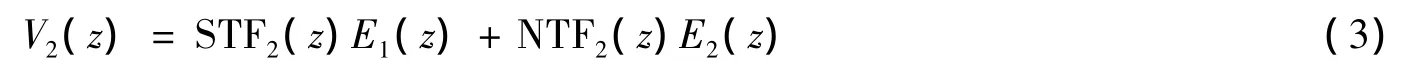
其中:STF2和NTF2为第二级的信号传递函数和噪声传递函数，可表示为:

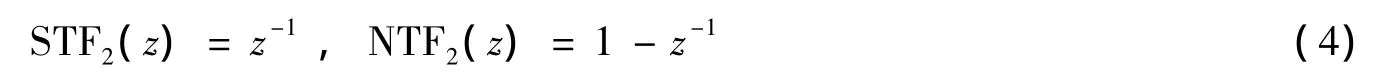
数字校正电路以两级输出信号V1和V2作为输入，并通过匹配消除第一级量化误差E1.从式(1)和(3)可得到匹配条件:

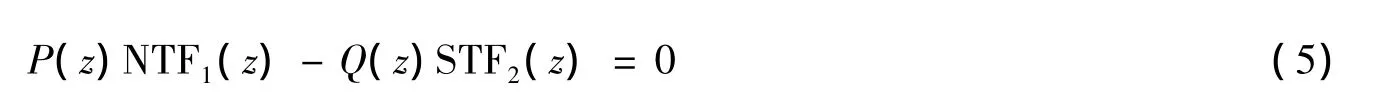
选择P(z)=STF2(z)和Q(z)=NTF1(z)，此时整体输出如式(6)所示，其噪声整形效果等效于三阶单回路SDM，但稳定性与二阶SDM相当(阶次越高稳定性越差).

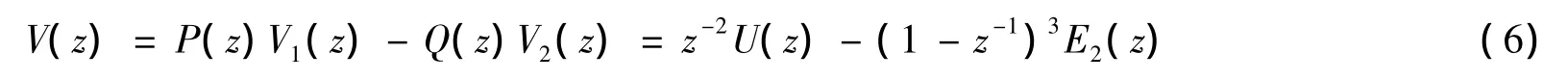
理想情况下通过式(5)设计的滤波器可以使SDM达到很好的信噪比.然而在实际情况下由于电路的采样时钟抖动、热噪声以及运算放大器参数(包括白噪声、有限直流增益、有限带宽、转换速率和饱和电压)的影响［5］，导致第一级量化误差E1无法完全抵消.另外，由于第二级调制器输入E1的幅值相对于第一级U小很多，因此第一级积分器的非理想因素占主导因素，第二级积分器可采用理想积分器进行模拟.综上所述，为了讨论方便仅假设第一级调制器参数具有不确定性，第二级调制器工作在理想情况下.此时设计问题可表述为:设计鲁棒滤波器Q(z)，使得级联SDM在非理想情况下工作时，Q(z)能满足以下优化问题:

其中:T(z)=z－1，NTF1a(z)表示非理想情况下第一级调制器的噪声传递函数.

为了求解式(7)的优化问题，首先将其转换为状态空间表达式的描述形式，并定义如下:

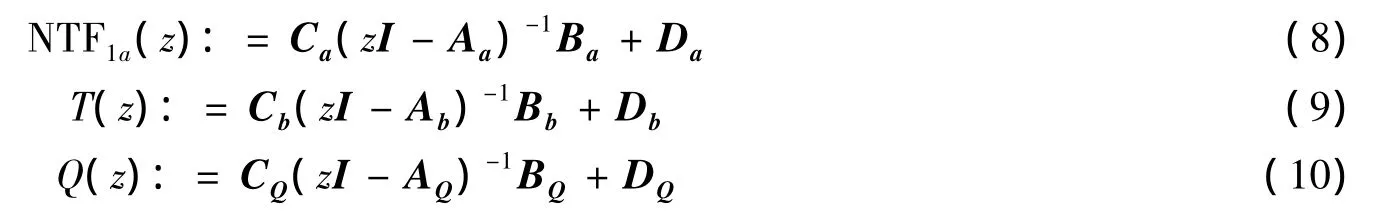
此时T(z)(NTF1a－Q(z))的状态空间描述为:

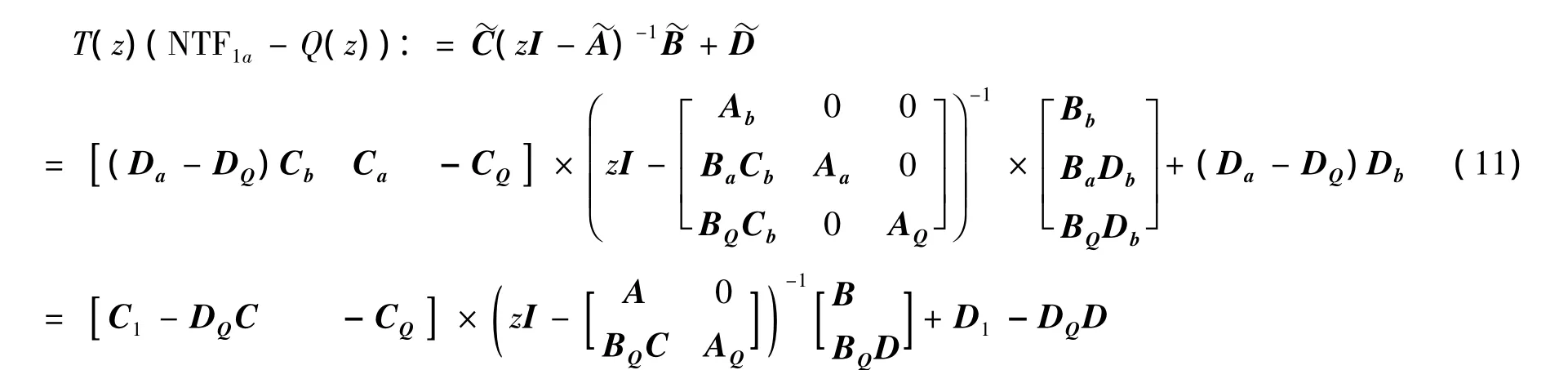
由于第一级调制器的非理想性，式(8)的参数将在一个动态范围内变化.通过MARKOV变换，将参数的摄动问题描述为区间矩阵，并利用LMI求解鲁棒滤波器，即求解以下问题:

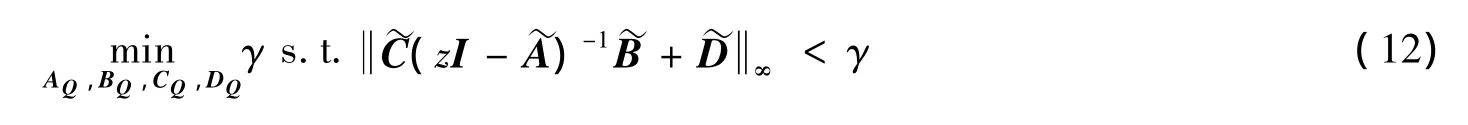
2 线性区间系统的MARKOV分析

考虑图1的系统，针对实际电路的非理想性，包括运放的有限增益和开关电容不匹配等问题，将积分器的非理想性表述为增益和极点的不确定性［6］.如前所述，本文主要分析第一级中二阶积分器的不确定性对系统的影响，H1(z)和H2(z)的传递方程可表述为:

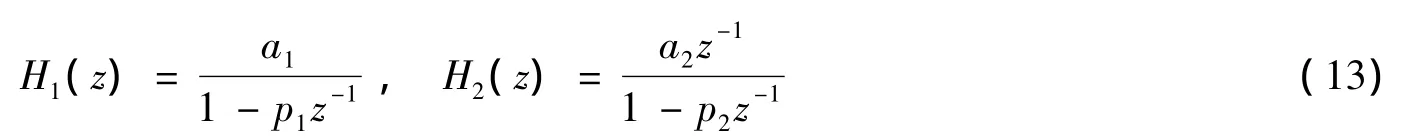
其中:a1，a2∈［amin，1］;p1，p2∈［pmin，1］.

此时式(8)的状态空间描述为:

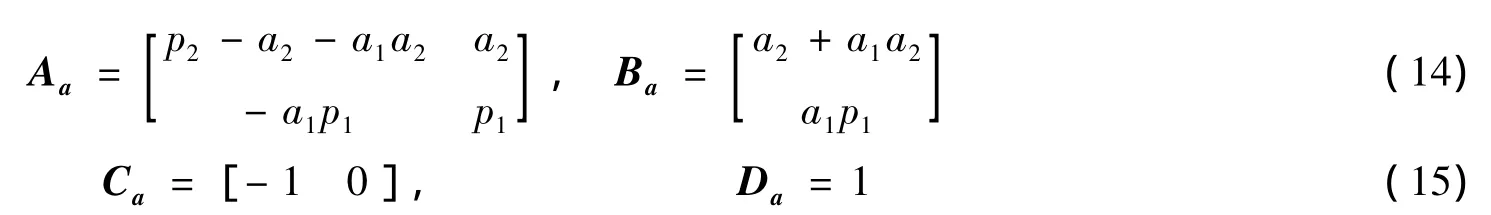
已知T(z)=z－1，式(9)的状态空间描述为:

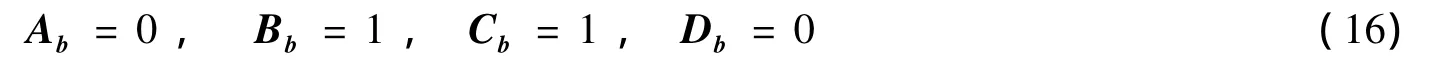
将式(14)～(16)代入式(11)中的矩阵可看出，系统的增益和极点不确定性仅对矩阵A产生影响，使矩阵A变为不确定矩阵.此时A可表示为:

根据MARKOV运算法则［7］，式(17)可描述为如下区间形式:

其中:

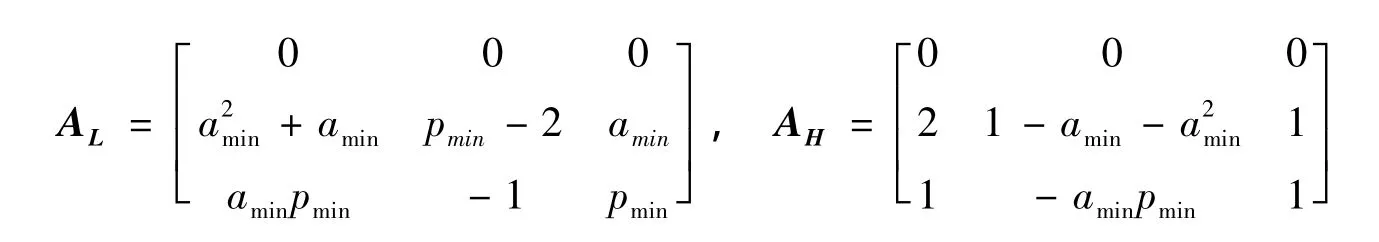
通过以上MARKOV运算，将系统参数不确定性描述成式(18)的区间矩阵形式.根据文献［8－9］，区间矩阵可等价描述为:

其中:A0=(AL+AH)/2，

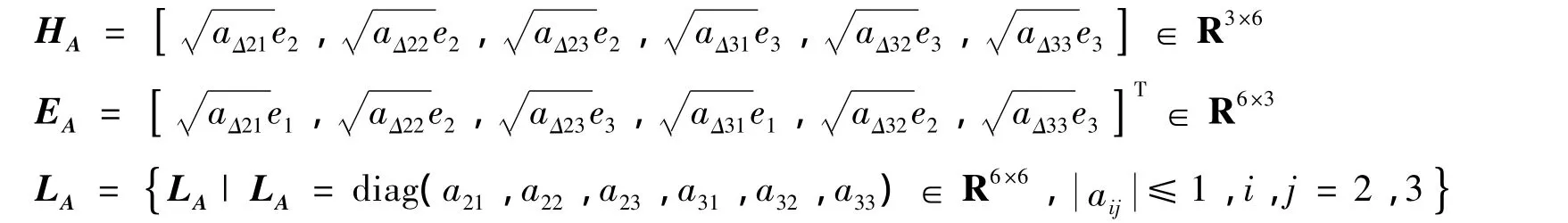
ei(i=1，2，3)为3阶单位矩阵的第i列，显然FA≤I.

同理有

其中:

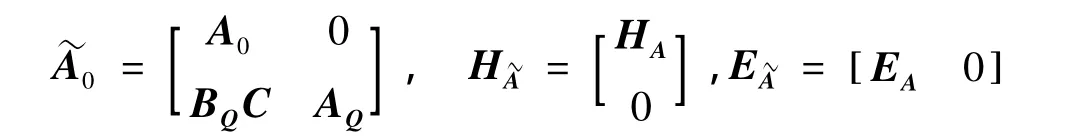
3 鲁棒H∞滤波器设计

给出线性系统在区间矩阵变化时鲁棒H∞滤波器可解的充分条件.在给出滤波器的构造方法之前，先提供以下引理.

引理1 假设滤波器(AQ，BQ，CQ，DQ)已知，对于在式(18)中的区间变化时，系统满足的充分条件是存在矩阵P=PT＞0以及G使得

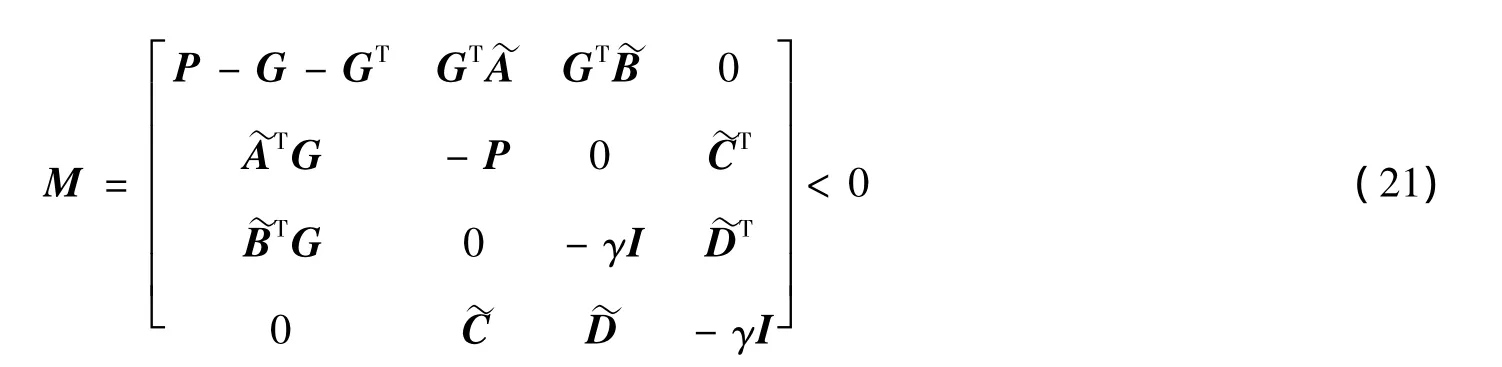
证明 引理1的证明可参考文献［10］中的定理2.

在引理1中，假设滤波器(AQ，BQ，CQ，DQ)是已知的，然而本研究的目的是设计滤波器满足式(12)的条件.也就是说式(21)中的滤波器参数(AQ，BQ，CQ，DQ)为需要确定的变量，因此式(21)实际上是一组非线性矩阵不等式.为了能够使用标准的LMI方法求解控制器［11］，现给出如下定理.

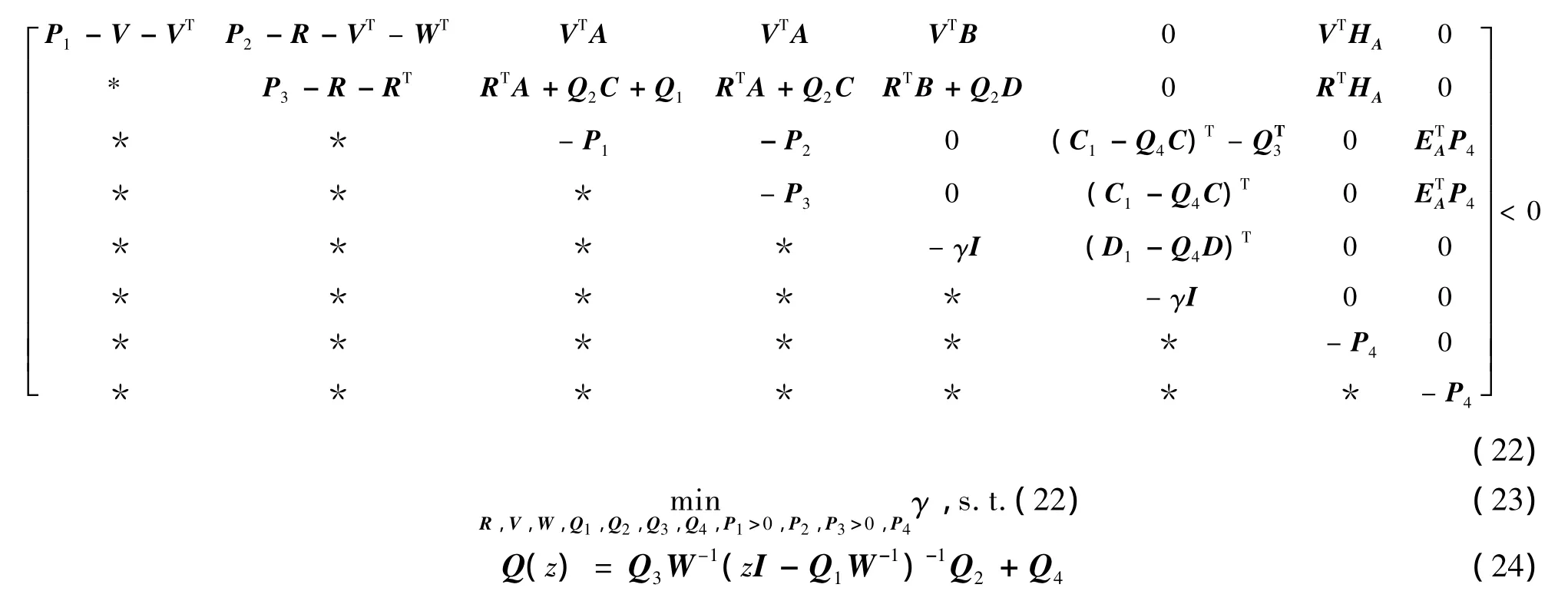
证明 首先将式(20)代入式(21)中，有:

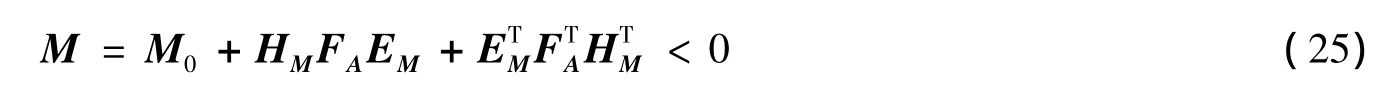
其中:

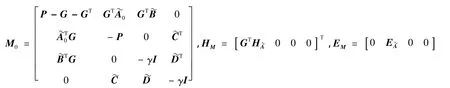
根据文献［12］，式(25)等价为:

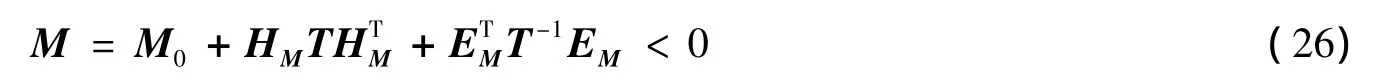
由Schur补引理可知，式(26)等价为:

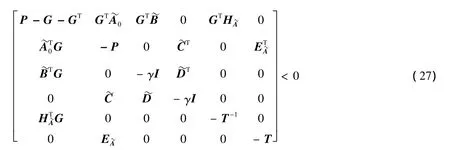
由式(27)很容易得出G+GT－P＞0，由P＞0可得出G+GT＞0且矩阵G是非奇异阵.可将G和G－1分解成如下形式:

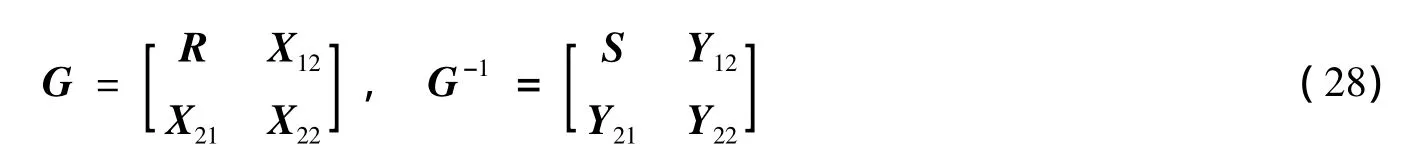
并作如下定义:

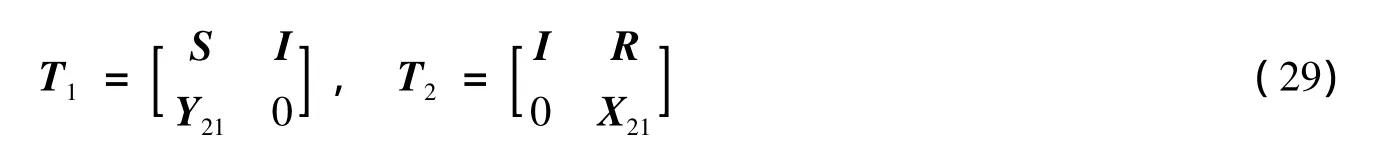
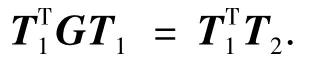
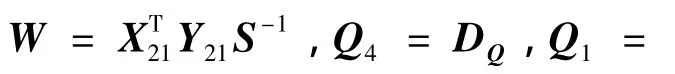
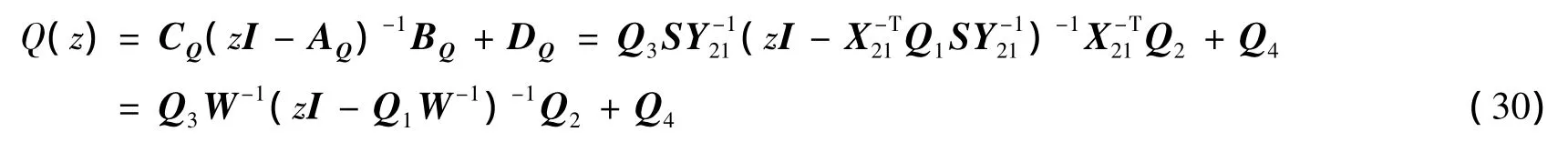
定理得证.

通过定理1可有效求解系统增益极点在给定区间变化时的滤波器设计问题.利用MATLAB中的LMI工具箱可求解式(23)的优化问题，并设计系统(10)中的全维和降维滤波器.

4 仿真分析

设计两种类型的校正滤波器，一种是通过定理1设计的滤波器，可用式(30)表示;另一种是根据公式(5)设计的滤波器(传统方式滤波器).为方便下文比较，假设式(14)中增益和极点变化程度相同，即a1=a2=p1=p2=gain_pole，并设系统增益极点变化下界amin=pmin=range.取range=0.95.根据定理1的描述，采用Matlab LMI Toolbox［13］(使用函数mincx)求解优化问题式(23)，可得到γ=0.100 4，滤波器为:

利用Matlab Simulink建立图1的仿真模型，调制器使用的是一位量化器，过采样率选为32，并将系统的非理想性表示为增益极点的不确定性.调用Delta－Sigma Toolbox［12］对建立的模型进行仿真(使用函数simulateSNR和calculateSNR)，其中输入信号为正弦波信号，计算输出信号的信噪比和功率谱密度.图2给出了输入信号幅值从－70 dB变化到0 dB时，非理想条件下(gain_pole=0.97)调制器输出的信噪比.从图2可看出，当不确定性参数在给定范围内变动且变化程度较大时，通过定理1设计的鲁棒滤波器比传统滤波器获得了更高的信噪比，整体的信噪比大约提高了5 dB，动态范围增加了10 dB(此时为70 dB).图3给出了此时级联2－1调制器输出比特流的功率频谱密度分布(输入幅值取－10 dB).从图3中可以看出，级联SDM的三阶噪声传递函数对量化噪声表现为高通特性，噪声在基带内得到很好的抑制.对高频部分噪声可通过后续数字滤波电路把带外噪声滤除，使系统信噪比得到提高.

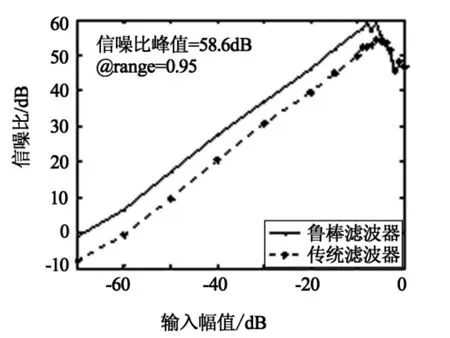
图2 gain_pole=0.97时输出信噪比Fig.2 Output SNR when gain_pole=0.97

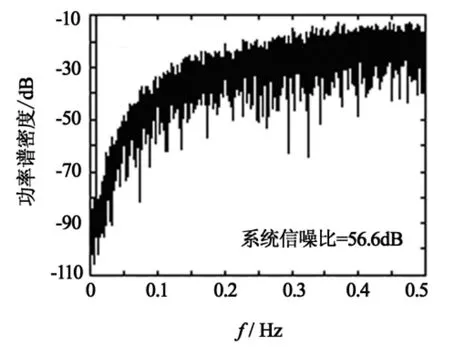
图3 级联结构输出的功率谱密度Fig.3 Output PSD of cascaded structure

进一步仿真表明，当系统不确定性变化程度较小、系统的增益极点与理想情况较为接近时，传统滤波器将表现出更好的性能，这是因为系统越接近理想情况将与传统滤波器的匹配程度越高.图4统计了非理想参数在［0.95 1］区间内变动时，鲁棒滤波器和传统滤波器输出的信噪比均差.可以看出，当非理想参数取值位于［0.984 1］之间时(将此区间称为鲁棒滤波器的盲区)，传统滤波器输出的信噪比将高于鲁棒滤波器.

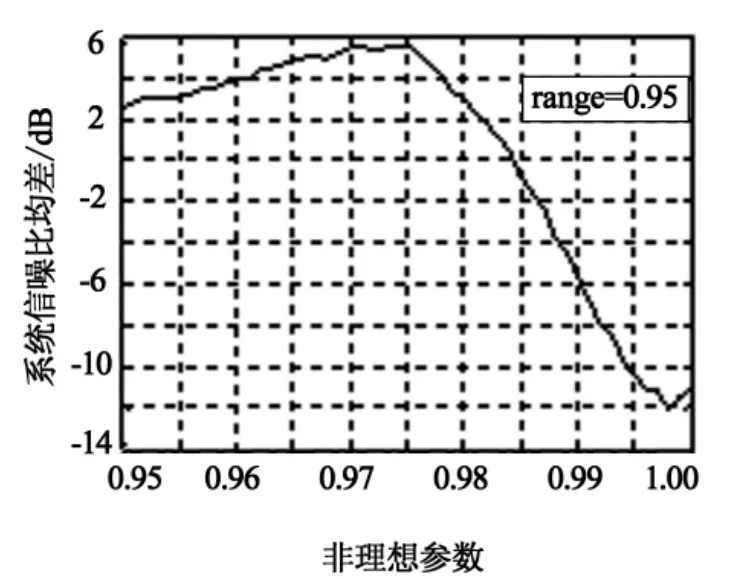
图4 range=0.95时两种滤波器输出信噪比均差Fig.4 Average deviation of output SNR between two filter when range=0.95

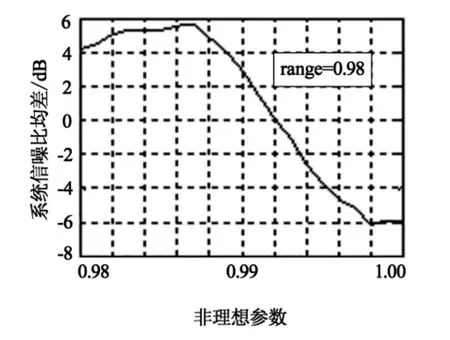
图5 range=0.98时两种滤波器输出信噪比均差Fig.5 Average deviation of output SNR between two filter when range=0.98

为了进一步提高非理想性参数在小范围内波动时鲁棒滤波器的性能，可重新设计滤波器.改变增益极点变化下界range=0.98，根据定理1重新进行LMI求解.此时γ=0.042 0，求得的滤波器为:

重新将求得的控制器代入系统进行仿真，仿真结果如图5所示.与图4比较可看出，此时鲁棒滤波器的性能有了很大的提升，盲区减少了50%(此时的盲区为［0.992 1］).非理想参数在［0 0.992］内变动时，鲁棒滤波器比传统滤波器获得了更好的性能.综合以上分析知，鲁棒滤波器适用于由低成本器件构成的调制器中，此时鲁棒滤波器能有效降低参数非理想性对性能的影响，提高输出信噪比并增加系统的动态范围.而传统滤波器更适合应用于采用高精度、昂贵调制器设计的电路中.

5 结语

对具有非理想性的级联Sigma－Delta调制器的鲁棒校正滤波问题进行研究，基于MARKOV理论，采用区间矩阵和线性矩阵不等式方法，给出了鲁棒滤波器存在的充分条件.仿真分析表明，当调制器偏离理想程度较大时，鲁棒滤波器比传统滤波器获得了更好的信噪比，因此鲁棒滤波器更适用于采用低成本电路构成的调制器中.

［1］张媛媛，姜岩峰.Σ－Δ模拟/数字转换器综述［J］.微电子学，2006，36(4):456－460.

［2］郭先清，林凡，吴孙桃.三阶级联Sigma－Delta调制器设计［J］.微电子学与计算机，2007，24(1):66－72.

［3］Yang Fu－wen，Gani Mahbub.An H∞approach for robust calibration of cascaded sigma－delta modulators［J］.IEEE Transactions on Circuits and Systems，2008，55(2):625 －634.

［4］Schreier R，Temes G C.Delta－Sigma data converters［M］.New Jersey:IEEE Press，1996.

［5］Temes G C.Finite amplifier gain and bandwidth effects in switched －capacitor filters［J］.IEEE Solid－ state circuits society，1980，15(3):358－361.

［6］Leger G，Rueda A.Cascade ΣΔ modulator with digital correction for finite amplifier gain effects［J］.Institution of Engineering and Technology，2004，40(21):1 322 －1 323.

［7］吴方向，史忠科，戴冠中.区间系统的H∞鲁棒控制［J］.自动化学报，1999，25(5):705－708.

［8］舒伟仁，张庆灵.区间广义系统的H∞鲁棒控制［J］.东北大学学报:自然科学版，2002，23(11):1 033－1 036.

［9］Markov S.An iterative method for algebraic solution to interval［J］.Applied Numerical Mathematics，1999，30(2):225 －239.

［10］Xie Li－hua，Lu Li－lei，Zhang David.Improved robust H2and H∞filtering for uncertain discrete－time systems［J］.Automatica，2004，40(5):873－880.

［11］Tan Z，Soh Y C，Xie L.Enveolpe－constrained H∞filter design:an LMI optimization approach［J］.IEEE Transactions on Signal Process，2000，48(10):2 960－2 963.

［12］王武，杨富文.线性区间系统的鲁棒非脆弱H∞控制［J］.集美大学学报:自然科学版，2005，10(2):109－113.

［13］Schreier R.Matlab delta sigma toolbox［EB/OL］.［2011 －12 －29］.MATLAB Central File Exchange，The MathWorks.http://www.mathworks.cn/matlabcentral/fileexchange/19.