基于变步长和内插的预失真系统LUT收敛算法

颜丽蓉，郭里婷

(福州大学物理与信息工程学院，福建福州 350116)

0 引言

作为新一代无线通信最具竞争力的技术，OFDM(正交频分复用)由于频谱利用率高、抗多径衰落能力强、抗噪声干扰能力强等优点在WLAN、DAB、DVB、HDTV等通信系统中得到了广泛的应用.但是，OFDM有较高的峰值平均功率比(简称PAPR)，这就要求功率放大器要有足够大的线性范围，否则，信号容易产生非线性失真，从而影响整个系统的通信性能.但该方法是以牺牲功率放大器的效率来换取其线性度，这与当今社会所倡导的绿色通信理念相背.因此，如何使得功率放大器高效率而又高线性度地工作已成为当今学术界和工程实践领域的研究热点.

功率放大器的线性化技术是解决其效率和线性度间矛盾的方案之一.迄今为止，已出现了多种改善功率放大器线性度的线性化技术:功率回退技术、前馈线性化技术、负反馈技术以及数字预失真技术等，各种线性化技术均有其优缺点.其中，数字基带预失真技术因无稳定性问题、精度高、适用于宽带通信、自适应能力强等优点最具发展前景［1］.

在给出基于LUT的预失真技术［2］传统的自适应预失真算法的同时，本研究针对查询表收敛速度慢的不足，对其进行相应的改进.并通过算法收敛曲线、星座图、功率谱密度以及BER性能的对比验证本文所改进算法的优越性.

1 OFDM系统中的数字基带预失真实现

预失真，即在信号进入放大器之前，先对信号进行非线性处理，该处理正好补偿了功率放大器对信号所造成的非线性影响，所以将两者级联后即可实现功率放大器的线性工作.OFDM系统中，预失真器接于滤波器和D/A转化器之间，包含预失真器的OFDM发射机框图如图1所示.

从实现框图可知，欲设计一预失真器，关键在于两方面:一个是功率放大器模型的确定;另一个则是自适应算法的确定.

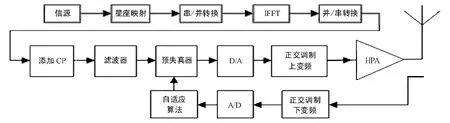
图1 OFDM系统发射机框图Fig.1 Transmitter block diagram of OFDM system

1.1 功率放大器的模型

目前，已有很多关于功率放大器的数学模型，总体而言，可分为两大类:无记忆功率放大器和有记忆功率放大器.由于本文侧重研究自适应预失真算法，因此选用结构较为简单的无记忆功率放大器模型.

在无记忆功率放大器模型中，广泛使用的有:针对行波管功率放大器的Saleh模型［3］和针对固态功率放大器的Rapp模型［4］.本文选用Saleh模型，其AM－AM和AM－PM特性函数分别如式(1)和式(2)所示.

式中:ρin为功率放大器输入信号的幅度值;αa、βa、αφ和βφ是模型参数，各个参数的经典取值为αa=2.151 8，βa=1.151 7，αφ=4.033 0，βφ=9.104 0.图2所示为Saleh模型的特性曲线仿真图.从图2中可以直观地看出，功放的输出幅度(AM输出)、输出相位(PM)与输入幅度(AM输入)之间存在着非线性关系，这也正是预失真所要解决的问题.

1.2 自适应算法

由于功放参数会随着温度、压强、湿度等环境因素的变化而变化，这就需要一个反馈回路去跟踪功放参数的变化，以实时更新预失真器的特性函数.自适应算法的应用则是实现这一过程的关键所在.常用的自适应算法有RASCAL［5］、LMS、RLS等，综合考虑算法实现的灵活性与复杂度，采用RASCAL算法.

RASCAL是Rotate and Scale的缩写，即它纠正的是信号所应旋转的角度和缩放的幅度.因此，进行RASCAL算法之前，需将信号由直角坐标转换为极坐标.设预失真器输入信号的幅度和相位分别为Vin和θin，功率放大器反馈回的信号幅度和相位分别为Vf和θf，则幅度环路误差和相位环路误差分别如式(3)和式(4)所示.

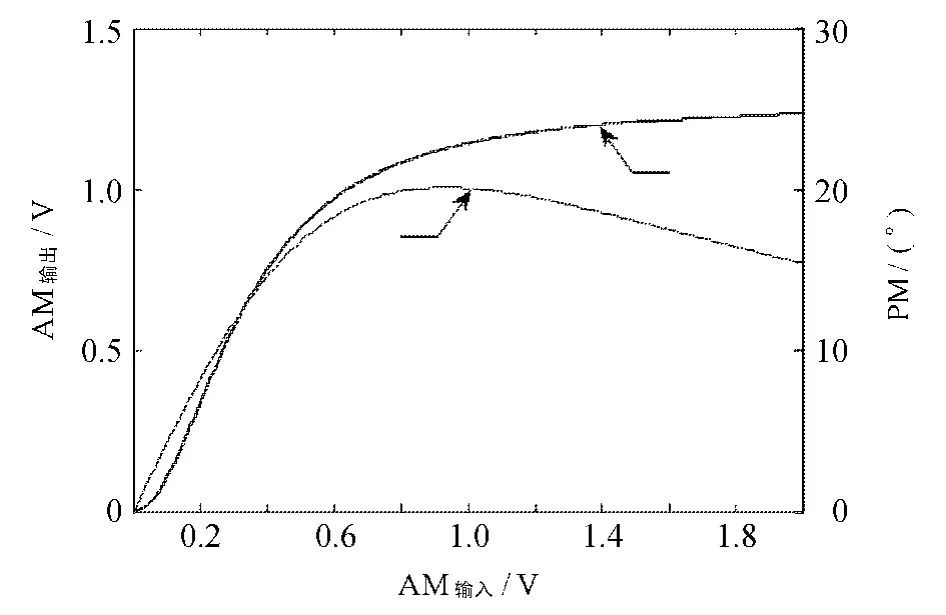
图2 Saleh模型AM－AM和AM－PM特性曲线Fig.2 AM －AM and AM －PM characteristic curve of Saleh model

式(3)中:K为功率放大器的理想放大倍数，由于本文所采用的是归一化的Saleh模型，因此K取1.RASCAL算法就是不断地比较预失真器的输入信号和功率放大器反馈回来的信号，根据环路误差Verror和θerror实时地对幅度表和相位表进行更新.

为补偿功率放大器的非线性，RASCAL算法利用递归的线性收敛式使式(3)和式(4)的误差最小化.查询表更新的递归方程如式(5)和式(6)所示.

式中:i表示查询表的地址;n表示迭代的次数;Si，n表示幅度查询表中地址为i的表项经过n次迭代后的值;Ri，n、α和β分别为幅度表和相位表收敛过程中的迭代步长，它们影响着查询表的收敛速度.

1.3 基于LUT的预失真器结构

基于LUT的预失真器的结构如图3所示.由于侧重的是预失真器的结构，因此将D/A转换和正交调制上变频等模块省略.

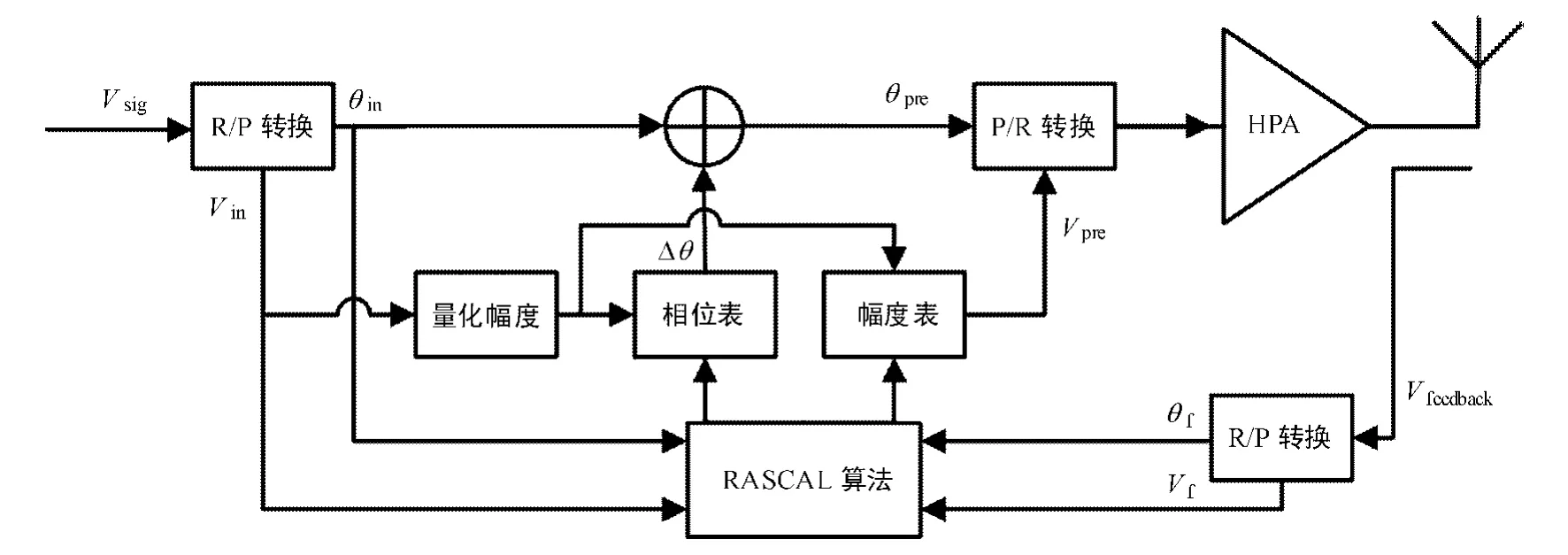
图3 基于LUT的预失真器结构Fig.3 Architecture of predistorter based on LUT

由图3可知，输入信号经直角坐标转换为极坐标后，分成两路.一路根据输入信号的幅度量化值对查询表进行索引进行预失真处理后通过功放，另一路则与功放输出端耦合反馈回来的信号在RASCAL算法的作用下更新查询表.幅度查询表和相位查询表并联连接，一方面在实现上难度较小，另一方面也使得幅度查询表和相位查询表各自收敛，相互间不受影响.

基于LUT的预失真技术是目前较为流行的预失真技术，因为该方法可用于任何增益波形图的功率放大器，并且线性化效果好.但是，查询表表项个数的多少决定了预失真效果的精度，为保证精度，表项个数需要足够大.另外，OFDM信号幅度服从瑞利分布［6］，动态范围较大，这样幅度经量化后就会产生大量的地址，整个查询表的更新需要大量的递归.所以，收敛速度慢是基于LUT的预失真技术的一大缺陷.

2 加快LUT收敛速度的方法及改进

为加快LUT的收敛速度，可从以下两个方面进行尝试:在自适应算法上，采用变步长的自适应算法;在查询表更新过程中，通过内插更新查询表内容.

2.1 变步长RASCAL算法

衡量自适应算法的优劣通常有两个方面:收敛速度以及稳态误差.但两者存在着矛盾，迭代步长的大小影响着收敛速度的快慢，迭代步长大的收敛速度较快，但同时稳态误差也较大，反之亦然.因此，必须在收敛速度和稳态误差间做好权衡，在保证稳态误差的前提下加快收敛速度.

为解决收敛速度和稳态误差间的矛盾，很多文献均提出了变步长的自适应算法的思想.归纳起来，这些算法大多是以误差或者信噪比为变量通过构造不同的函数形式来确定每次递归运算时所用迭代步长的大小.但由于大多数文献讨论的变步长算法适用于接收端的自适应滤波器，即其接收的是发送端发来的经过复杂信道的信号，因而其所构造的函数形式也较为复杂.考虑到自适应预失真中反馈回来的信号是经放大器耦合下来的，始终在发送端，其经过的信道突变性不大，因而采用适合于自适应预失真器的简单容易实现的变步长RASCAL算法，即在算法刚开始进行迭代时，选用比较大的步长，当算法基本收敛后，则选用比较小的步长.其流程图如图4所示.

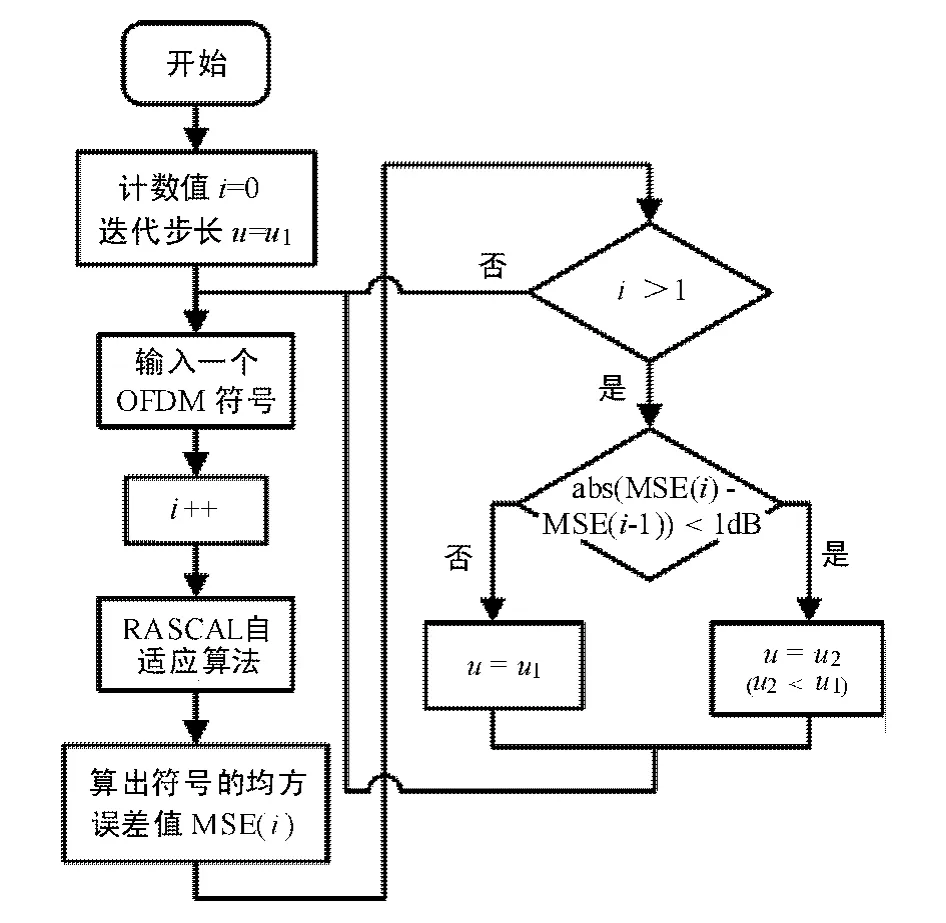
图4 变步长RASCAL算法流程图Fig.4 Flowchart of variable － step RASCAL

2.2 LUT内插算法及改进

因为功率放大器的特性曲线是连续平滑的，所以若将其量化成离散的点后，相邻点间的值具有一定的相关性.鉴于此，文献［6］提出通过线性内插来提高查询表的收敛速度，其基本思想为:首先，构造一个与查询表大小一致的1bit地址指示器，初始化时除最小和最大地址置1外，其它均置0;对于输入信号，算出其量化幅度值address，根据RASCAL算法对地址为address的幅度查询表和相位查询表的表项值进行更新，同时地址指示器相应地址address置1;接着，从地址address向下和向上查找地址指示器中距离address最近且已经置1了的地址address－La和address+Lb;最后，利用已找出的三个地址所对应的查询表的值对address－La和address之间、address和address+Lb之间的幅度查询表和相位查询表的表项值进行线性内插.

文献［7］分析并通过仿真指出文献［6］所用方法并不能使收敛速度有所改善，该方法在通常情况下只起到“平滑”的作用.鉴于此，通过以下两个方面对其进行改进:第一，地址指示器初始化时均置为0，并且在查询表更新过程中，除量化幅度值所对应的地址指示器地址置1外，通过内插得到的表项值所对应的地址指示器地址也置1;第二，采用二阶拉格朗日内插代替线性内插.这是因为对于自适应算法来说，迭代初始值是非常重要的，初始值与理想值越接近，则算法越容易收敛.若用文献［6］所述算法，则初始值将不断变化，因其只对量化幅度值所对应的地址指示器地址置1，且由于其为线性内插，与Saleh功放的反特性曲线差距较大，这样会使得算法在收敛过程中误差起伏大，反而使收敛效果变差.采用的二阶拉格朗日内插与Saleh功放的反特性曲线更为接近，因此，经改进后的算法所确定出的进行自适应算法的初始值更为接近理想值，并且算法初始值一经确定就不会再变化.

拉格朗日插值法是基于基函数的插值方法，n阶拉格朗日插值多项式可表示为:

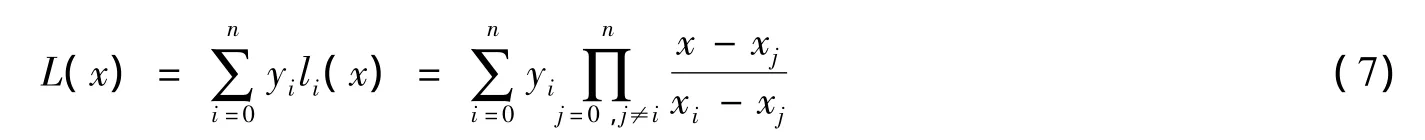
式中:li(x)为i次基函数;点(xi，yi)(i=0，1，…，n)为插值点，n取2.

3 仿真结果与分析

基于中国数字电视地面广播DTMB标准多载波模式对所改进算法进行仿真验证，所用仿真软件为Matlab，仿真在AWGN信道下进行，OFDM子载波数为3 780个，保护间隔采用PN420模式，星座映射模式为16QAM，查询表大小为256.通过对比固定步长条件下不加内插、固定步长条件下加线性内插、固定步长条件下加拉格朗日内插、变步长条件下不加内插、变步长条件下加线性内插以及变步长条件下加拉格朗日内插在算法收敛曲线、星座图、功率谱密度图和误比特性能的仿真结果进行分析讨论.

3.1 算法收敛曲线

通过仿真并统计分析得出:以算法的稳态误差为基准，迭代步长在［0.1 0.2］范围内稳态误差会较小，而以收敛速度为基准，迭代步长在［0.7 0.8］范围内收敛速度会较快.所以分别选取迭代步长u=0.12、u=0.75的固定步长算法以及刚开始迭代步长u=0.75，到基本收敛时，u=0.12的变步长算法三种不同条件来验证本文所提出的变步长算法的优越性.

图5所示为系统在不同算法条件下得到的算法收敛曲线.从图5(a)可知，在保证稳态误差的前提下，变步长的RASCAL算法有效提高了算法的收敛速度.要达到相同的稳态误差，固定步长算法需要20个符号左右才能收敛，而变步长算法只需7个符号左右就收敛了.

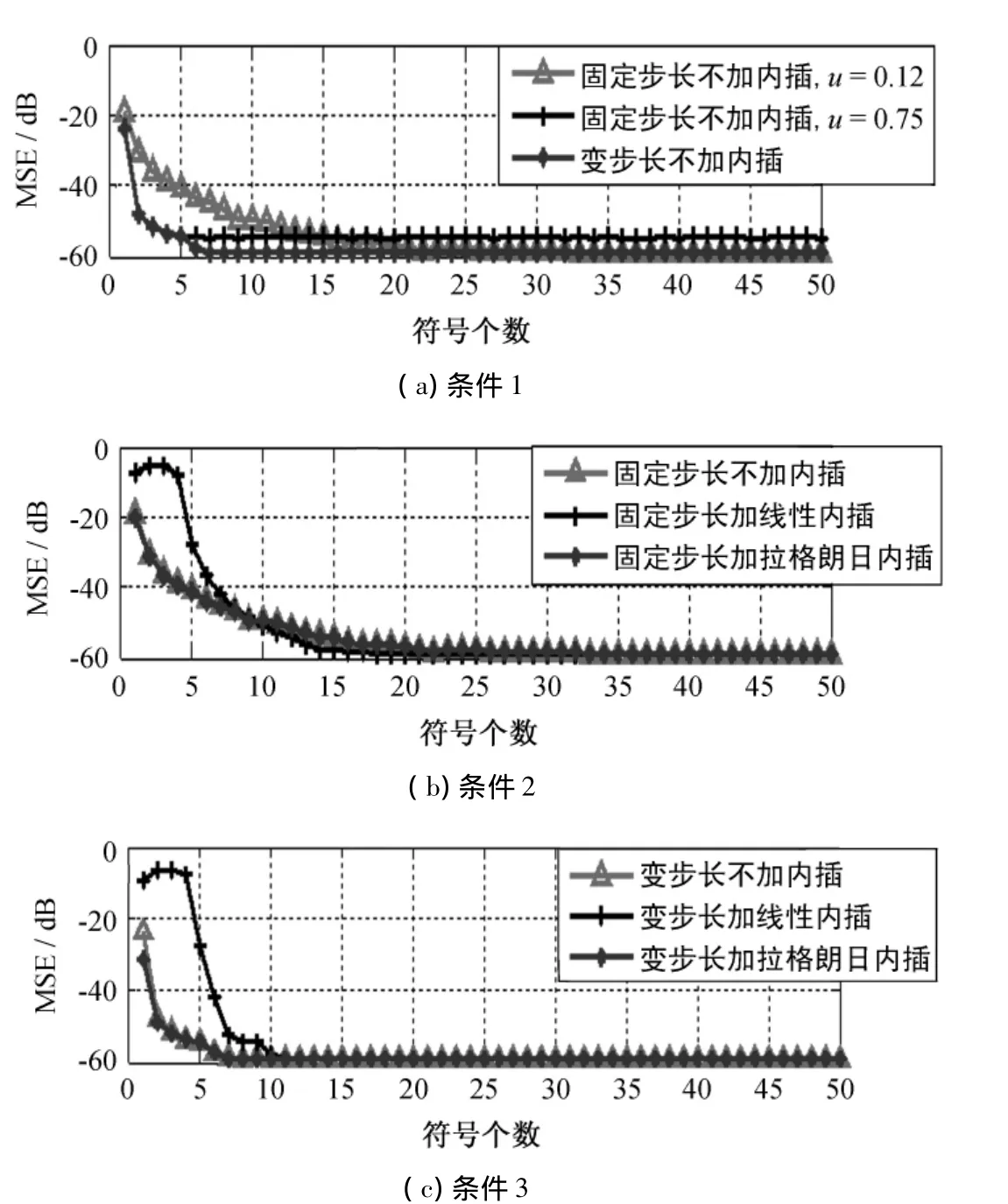
图5 不同算法条件下的MSE曲线Fig.5 MSE curves in different algorithms

对比图5(b)和图5(c)可知，正如前面所分析，由于线性内插使得算法的初始值不固定，从而导致在算法收敛的过程中，符号误差起伏大.在算法的收敛过程中，线性内插得到的符号MSE值均大于不加内插以及拉格朗日内插情况下的MSE值.而拉格朗日内插的使用则使算法的初始误差值保持在原来水平或者更小，从图5(c)可看出，相较于不加内插的情况，拉格朗日算法的初始MSE值减小了约10 dB.

3.2 星座图、功率谱以及误比特性能

图6、图7、图8所示分别为系统在不同算法条件下所得的星座图、功率谱密度图以及误比特率性能图.从图中可看出，因为功放的非线性作用，时域上信号星座图发生偏转、扩散，产生云团效应，频域上信号功率谱的带内、带外差距变小，功率谱带外扩展严重，严重影响系统的误比特性能.所用的几种算法均消除了星座图的云团效应，使功率谱的恶化情况有所改善，提高了系统的误比特性能.

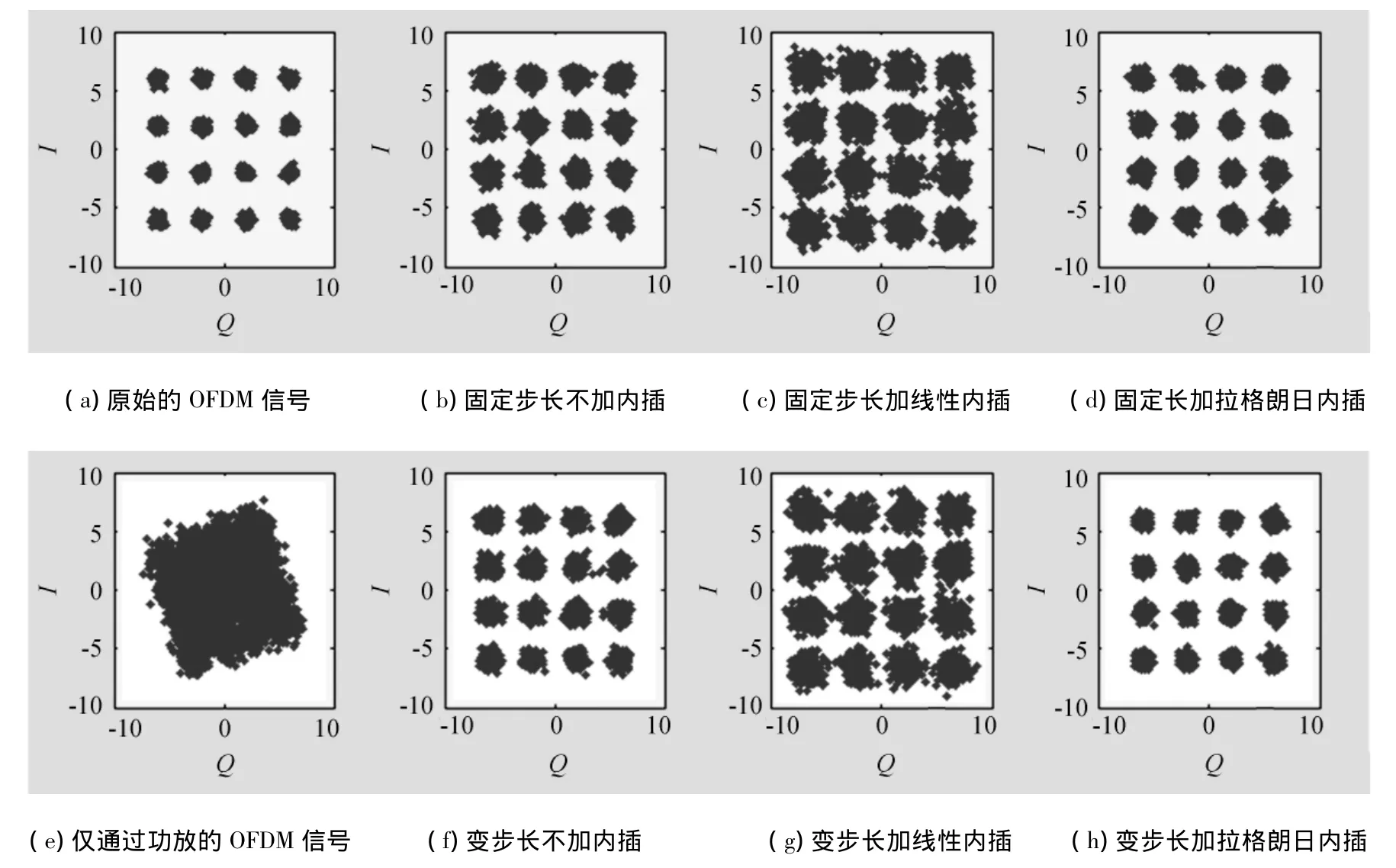
图6 不同算法条件下的星座图Fig.6 Constellations in different algorithms

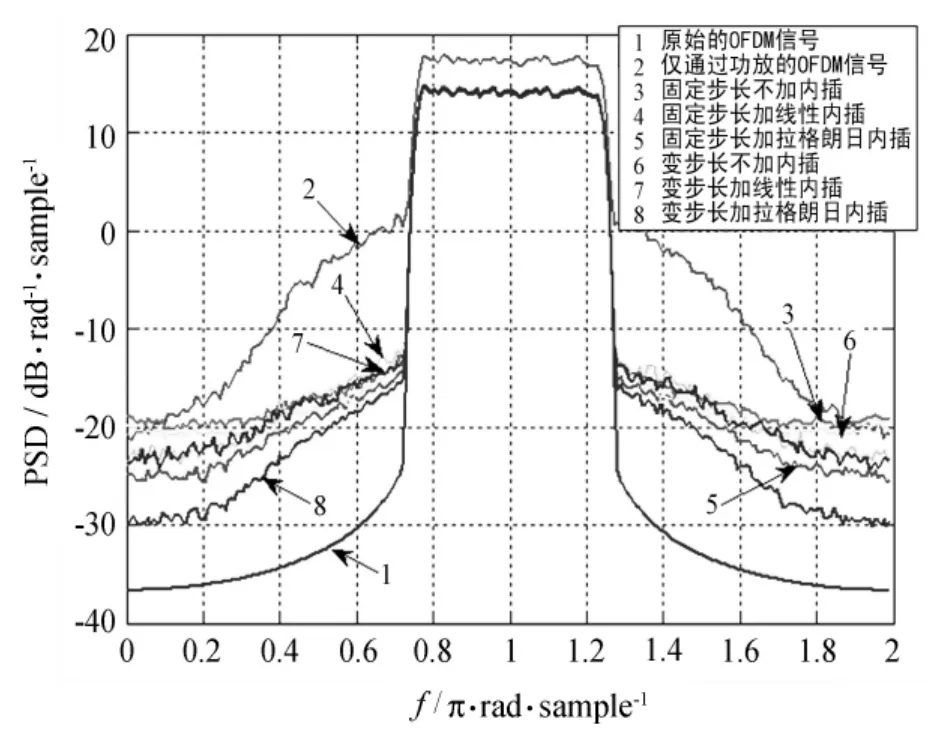
图7 不同算法下的功率谱密度图Fig.7 PSDs in different algorithms

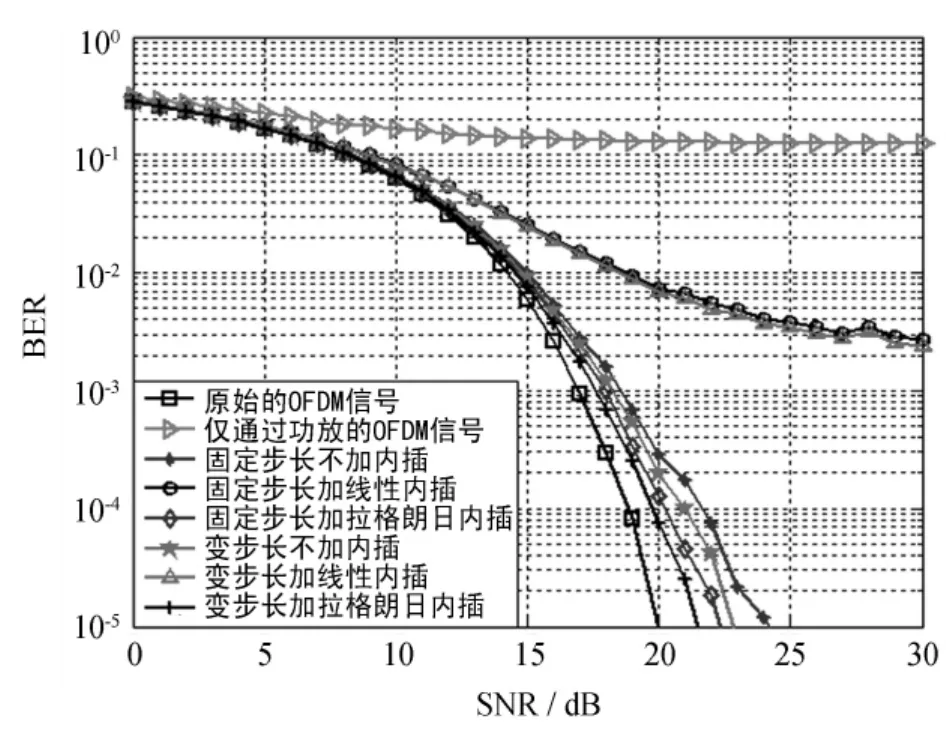
图8 不同算法下的误比特率性能Fig.8 BERs in different algorithms

总体来说，变步长条件下对功放的非线性改善效果要优于固定步长情况下的，拉格朗日内插的改善效果优于不加内插的，而线性内插改善效果反而低于不加内插以及拉格朗日内插的情况，这与前面收敛曲线的仿真结果是相吻合的.通过对比可知，本文所改进的算法，即变步长情况下加拉格朗日内插对于功放的非线性补偿效果最佳.

4 结语

针对基于LUT的预失真技术查询表收敛速度慢的缺陷，通过两方面对其进行改进:一方面，采用变步长的RASCAL算法，在保证算法稳态误差的同时，提高算法的收敛速度;另一方面，在查询表收敛过程中，对其进行拉格朗日内插，以优化自适应算法的迭代初始值.经MATLAB仿真，通过算法收敛曲线、星座图、功率谱以及误比特性能的对比，仿真结果均一致性地说明了本文所改进算法又好又快地补偿了功率放大器的非线性影响，在系统误比特率提高不大的前提下，减小了信号功率谱的带内损耗，降低了信号功率谱的带外扩展，从而使得功率放大器高效率而又高线性度地工作.

［1］艾渤，李波，钟章队，等.宽带功率放大器预失真原理［M］.北京:科学出版社，2011:5－8.

［2］Muhonen K J，Kavehrad M，Krishnamoorthy R.Look－up table techniques for adaptive digital predistortion:a development and comparison［J］.IEEE Transactions on Vehicular Technology，2000，49(5):1 995 －2 002.

［3］Rapp C.Effects of HPA－nonlinearity on 4－DPSK－OFDM signal for a digital sound broadcasting system［C］//Proc 2nd European Conference on Satellite Communications.Liege Belgium:［s.n.］，1991，2:179 －184.

［4］Saleh A，Salz J.Adaptive linearization of power amplification in digital radio systems［J］.Bell System Technical Journal，1983，62(4):1 019－1 033.

［5］Wright A S，Durtler W G.Experimental performance of an adaptive digital linearized power amplifier［C］//IEEE MTT －S Digest.Albuquerque:［s.n.］，1992:1 105 －1 108.

［6］Wesolowski K，Pochmara J.Efficient algorithm for adjustment of adaptive predistorter in OFDM transmitter［C］//IEEE 52nd VTC’2000.Boston:［s.n.］，2000，5:2 491 －2 496.

［7］艾渤，杨知行，潘长勇，等.基于LUT的HPA数字基带预失真方法研究［J］.电子与信息学报，2007，29(7):1 580－1 583.