Hilbert空间中无冗g－框架与g－Riesz基的关系

黄华美，朱玉灿

(福州大学数学与计算机科学学院，福建福州 350116)

0 引言

Hilbert空间中框架的概念是由Duffin和Schaeffer在1952年研究非调和Fourier级数时提出［1］，当时并没有得到什么发展.直到1986年，Daubechies，Grossmann和Meyer突出的贡献［2］，使框架研究吸引了很多学者的目光.随着对框架理论研究的不断深入，许多学者对框架理论进行了各种推广.孙文昌教授在文献［3］中提出了一种更为一般的框架概念即g－框架.g－框架的提出为框架的发展提供了另一个方向，在研究的过程中发现两者存在着很多的不同.在框架理论中成立的一些定理在g－框架中并不成立.其中之一是在框架理论中的无冗框架与Riesz基是等价的，而在g－框架理论中无冗g－框架与g－Riesz基是不等价.本文主要从两个方面比较了两者的差别.首先g－Riesz基可以用线性无关等价刻画，举例说明了无冗g－框架可以是线性相关的.其次从无冗g－框架与g－Riesz基的两个等价刻画中发现g－Riesz基所要求的条件比无冗g－框架强.最后给出无冗g－框架的另一等价刻画及讨论了fusion框架的扰动.

设U，V是两个复Hilbert空间，其内积为＜·，·＞，范数为 ·，{Vj}j∈J是U的闭子空间序列，其中J是整数集Z的子集，L(U，Vj)表示U到Vj的所有有界线性算子的全体.定义线性空间:

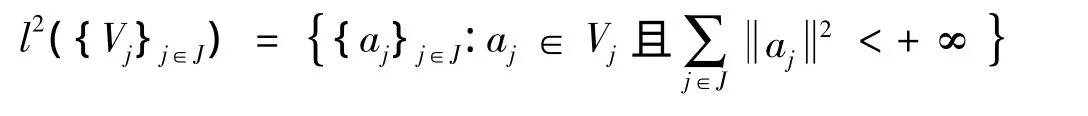
和内积＜·，·＞:

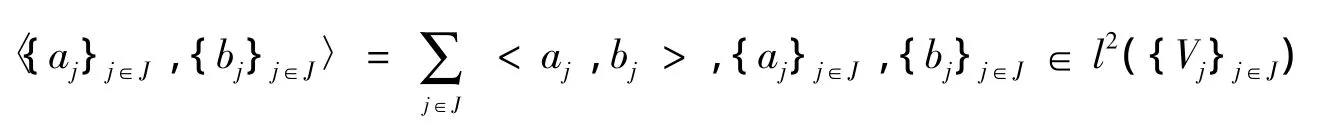
则l2({Vj}j∈J)是一个复的Hilbert空间.

定义1 序列{Λj:Λj∈L(u，Vj)}j∈J称为Hilbert空间U关于{Vj}j∈J的g－框架，如果存在A，B＞0，对任意的f∈U有

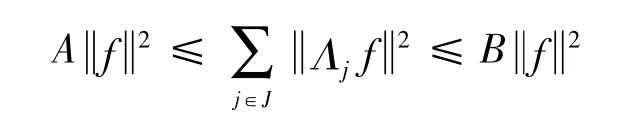
成立，称A，B分别为g－框架的下界和上界.

若仅有右边不等式成立，则称{Λj}j∈J为U关于{Vj}j∈J的g－Bessel序列.

如果A=B=λ，则称为紧g－框架.若λ=1，则称为g－Parseval框架.

定义2 序列{Λj:Λj∈L(U，Vj)}j∈J称为U关于{Vj}j∈J的无冗 g－框架，如果{Λj}j∈J是U关于{Vj}j∈J的g－框架但去掉任意一个元素就不是U关于{Vj}j∈J的g－框架.

定义3［3］序列{Λj}j∈J称为Hilbert空间U关于{Vj}j∈J的g－Riesz基，如果满足下列两个条件:

1){Λj}j∈J是g－完备的即{f∈U:Λjf=0，j∈J}={0};

2)存在正数A，B使得对任意有限集合J1⊂J和任意gi∈Vj，j∈J1有

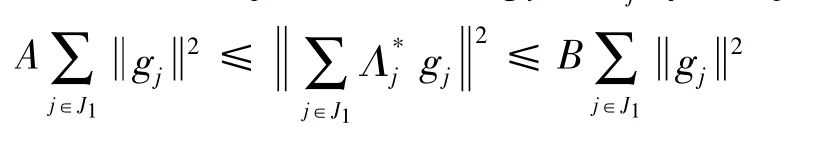
1 无冗g－框架与g－Riesz基的关系

引理1 设Λj∈L(U，Vj)，j∈J.则下列两个叙述等价:

1)序列{Λj}j∈J是U关于{Vj}j∈J的 g － Riesz基且界为A，B.

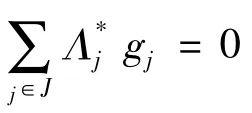
由引理1知g－Riesz基一定是线性无关的，但无冗g－框架却不一定是线性无关.

例1 设{en}∞n=1为Hilbert空间U的标准正交基，定义有界线性算子Λi:U→C2其中:

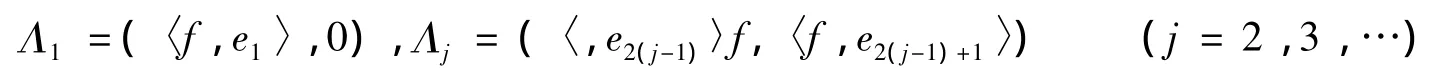
则对任意的f∈U，有

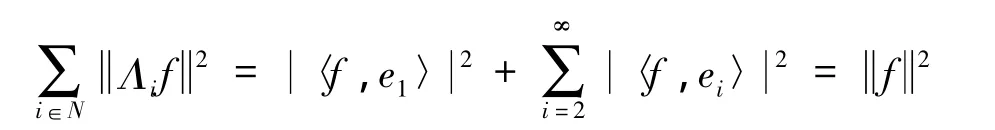
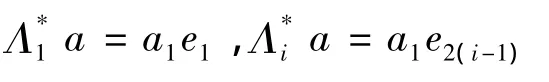
以上是无冗g－框架与g－Riesz基的第一个不同之处，接着给出两者的不同的等价刻画.先给出一个引理.

引理2 设Λj∈L(U，Vj)，则下面两个条件等价:

1)序列{Λj}j∈J是U关于{Vj}j∈J的无冗g－框架，且

2)序列 {Λj}j∈J是U关于{Vj}j∈J的 g － Riesz基.

定理1 序列{ΛJ}j∈J是U关于{Vj}j∈J的g－框架，以下结论等价:

1)序列{Λj}j∈J是U关于{Vj}j∈J的无冗 g－框架.

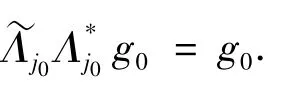
证明 必要性 由文献［6］知结论成立.

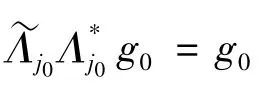
定理2 序列{Λj}j∈J是U关于{Vj}j∈J的g－框架，以下结论等价:

1)序列{Λj}j∈J是U关于{Vj}j∈J的 g － Riesz基.

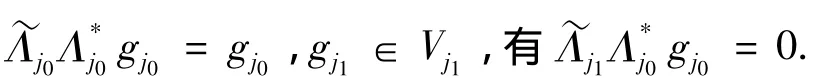
证明 必要性 由{Λj}j∈J是U关于{Vj}j∈J的g－Riesz基，知对任意的j1，j2∈J，gj1∈Vj1，gj2∈Vj2由引理2知

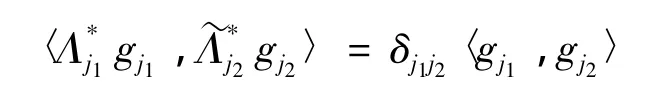
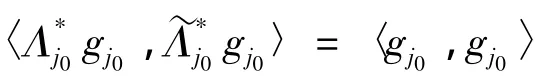
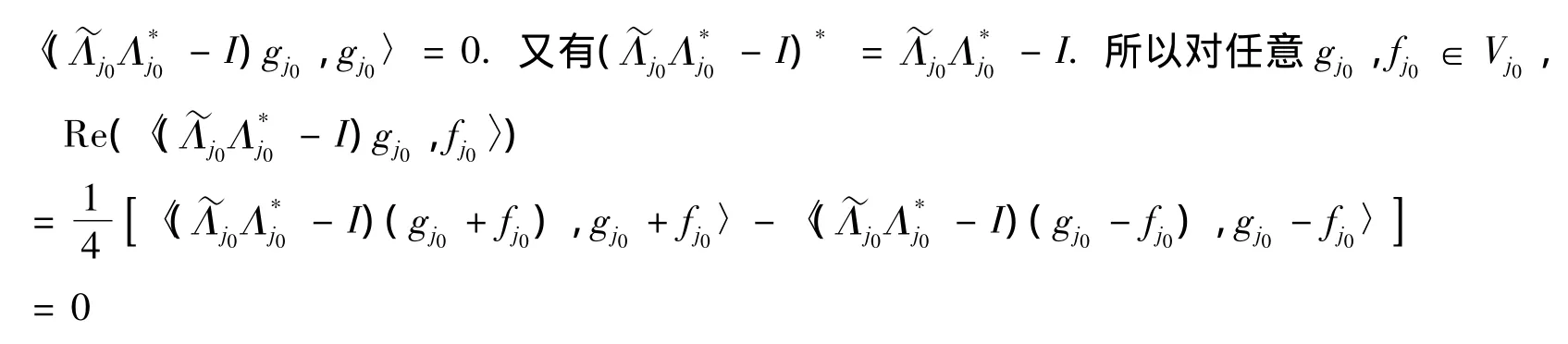
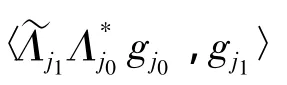
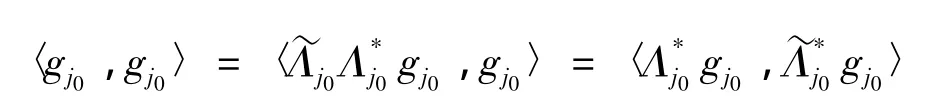
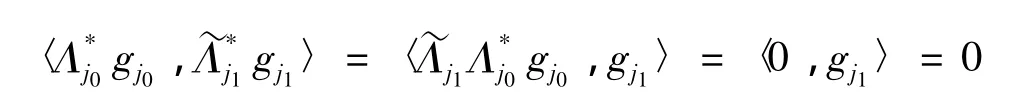
注1 由定理1及定理2可以看到无冗g－框架与g－Riesz基之间的差别.无冗g－框架成立的条件要弱很多.

下面给出无冗g－框架的另一等价刻画.

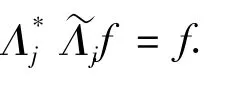
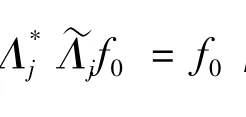
引理3 设H，K为Hilbert空间，T:H→K为有界线性算子，则以下结论等价:

1)T为单射且T(H)为闭子空间.

2)存在常数c＞0使得对任意的f∈H有Tf≥cf.

引理4［7］序列{Λ}是U关于{V}的g－框架，令T:U→U是U的可逆算子，则{ΛT}是U

jj∈Jjj∈Jjj∈J关于{Vj}j∈J的g－框架.

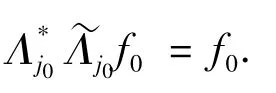
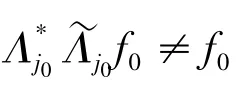
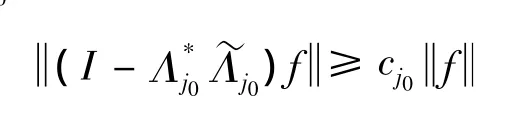
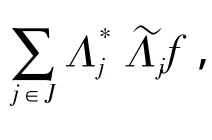
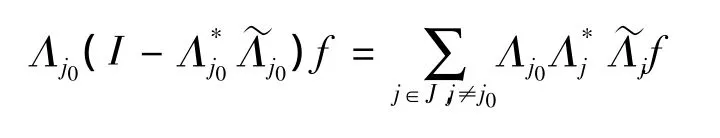
又有

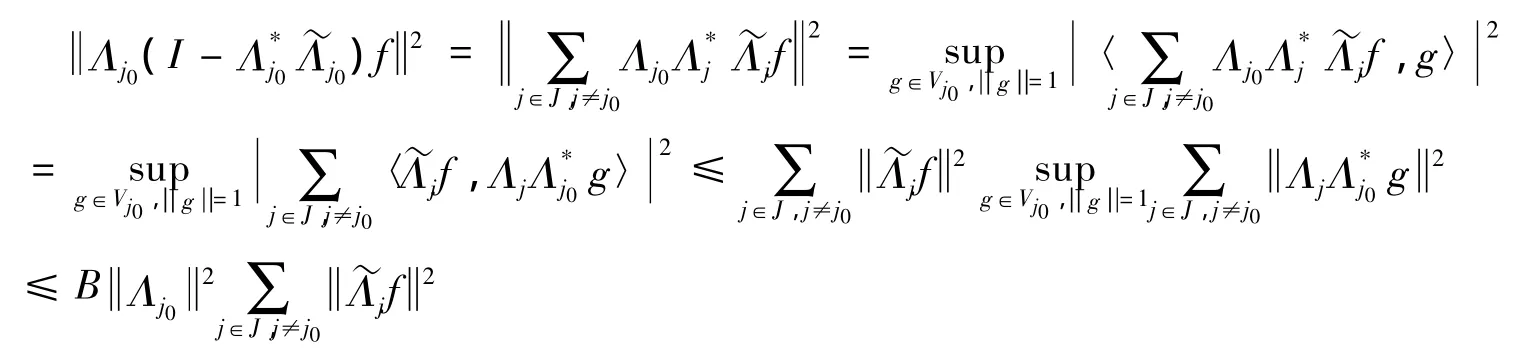
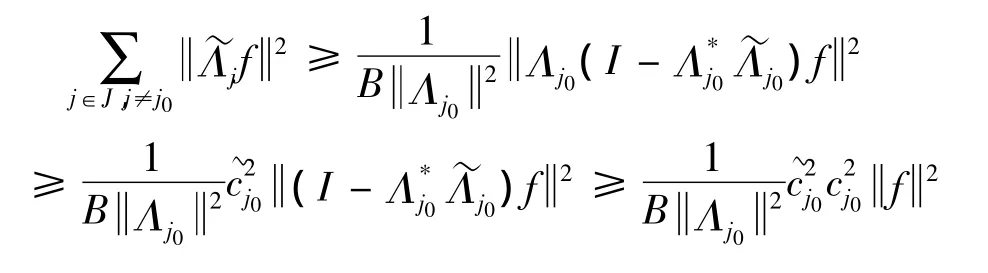
2 fusion框架的扰动

fusion框架是g－框架的一种特殊情况.fusion框架的特殊性在于其算子是空间到子空间上的正交投影而不是g－框架中的有界线性算子.正是由于fusion框架的特殊性，使得fusion框架有很多不同的结论.

设W是H的闭子空间，用πWj表示H到Wj的正交投影.

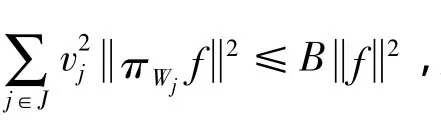
如果A=B，则称{(Wj，vj)}j∈J为H的紧fusion框架.

如果A=B=1，则称{(Wj，vj)}j∈J为H的 Parseval fusion框架.

在文献［9］定理2中对fusion框架中的不带权的扰动进行了讨论，在文献［10］中定理4.3对fusion框架的带有相同的权重的扰动进行了讨论.下面将对fusion框架带不同权的扰动进行讨论.

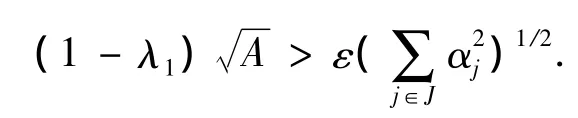
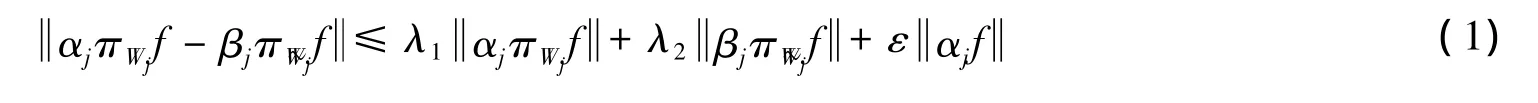
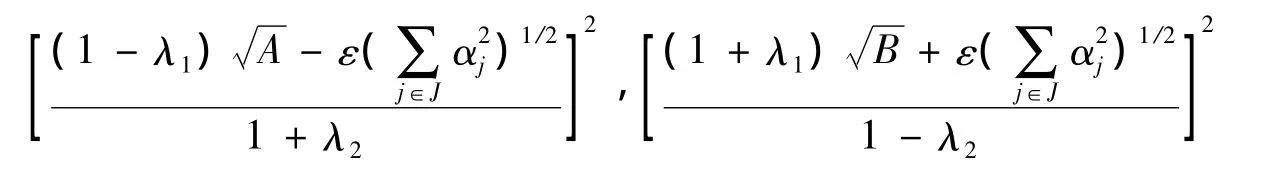
证明 由(1)式得对任意的f∈H，j∈J有

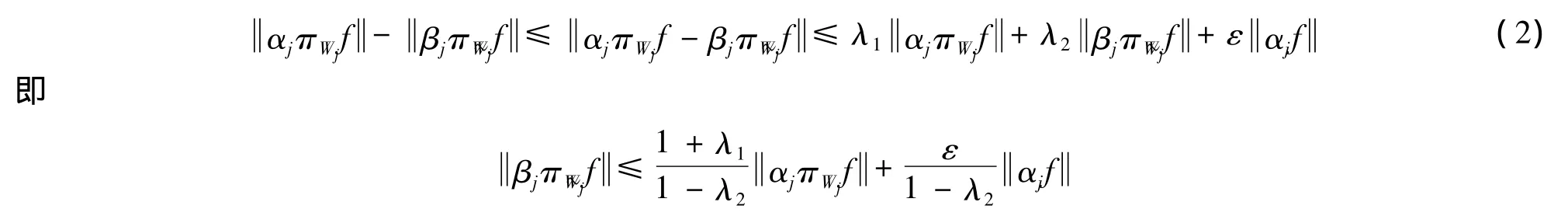
从而对任意f∈H，有

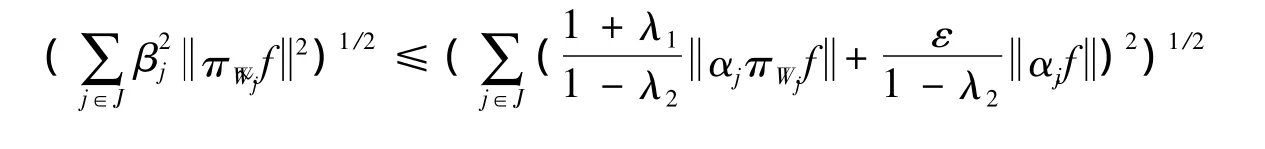
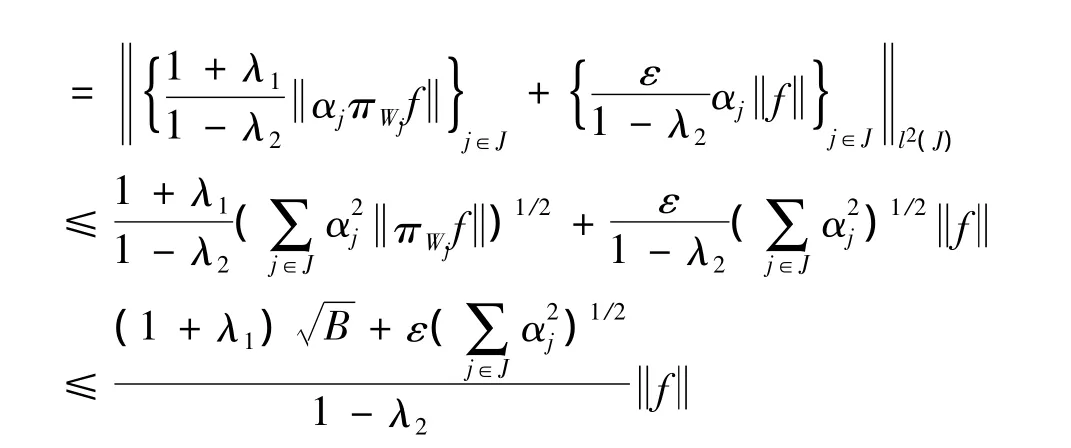
另一方面，对任意f∈H，j∈J，由(2)式得

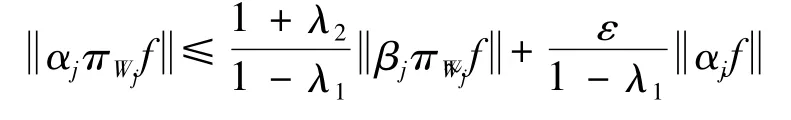
类似的，对任意f∈H，有

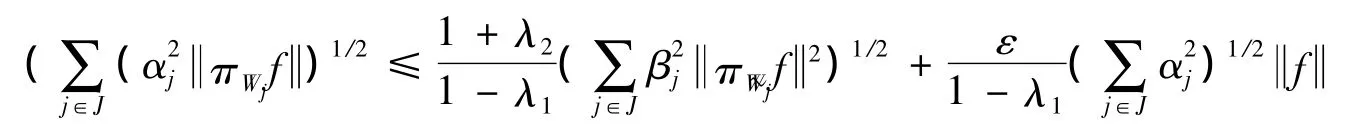
故此对任意f∈H，有

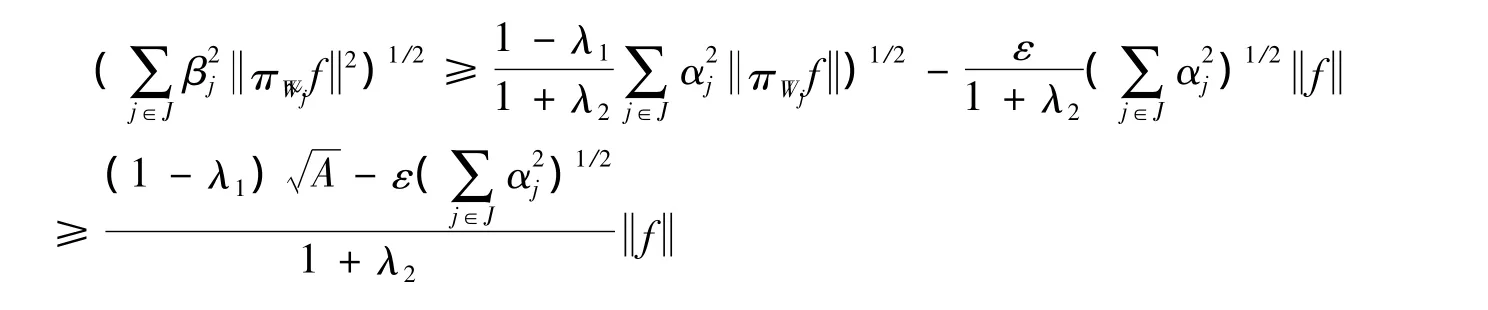
［1］Duffin R J，Schaefief A C.A class of nonharmonic Fourier series［J］.Transactions of the American Mathematical Society，1952，72(2):341－366.

［2］Daubechies I，Grossmann A，Meyer Y.Painless nonorthogonal expansions［J］.Journal of Mathematical Physics，1986，27(5):1 271－ 1 283.

［3］Sun Wen－ chang.G －frames and g－Riesz bases［J］.Journal of Mathematical Analysis and Applications，2006，322(1):437－452.

［4］Zhu Yu－can.Characterizations of g－frames and g－Riesz bases in Hilbert spaces［J］.Acta Mathematica Sinica:English Serires，2008，24(10):1 727 －1 736.

［5］Li Jian－zhen，Zhu Yu－can.Exact g－frames in Hilbert spaces［J］.Journal of Mathematical Analysis and Application，2011，374(1):201－209.

［6］丁明玲，朱玉灿.Hilbert空间中的无冗g－框架［J］.福州大学学报:自然科学版，2010，38(4):461－467.

［7］王静，高德智.g－框架的摄动和原子分解［J］.数学物理学报，2010，30(6):1 451－1 456.

［8］Casazza P G.Kutyniok G.Frame of subspaces［J］.Contemporery mathematics，2004，345(1):87 －114.

［9］Casazza P G，Kutyniok G，Li Shi－ dong.Fusion frames and distributed processing［J］.Applied Computational Harmonic A-nalysis，2008，25(1):114－132.

［10］Khosravi A，Musazadeh K.Fusion frames and g－frames［J］.Journal of Mathematical Analysis and Application，2008，342(2):1 068－1 083.