基于改进粒子群算法参数优化的APF预测电流控制

陈东毅，陈冲

(福州大学电气工程与自动化学院，福建福州 350116)

有源电力滤波器(APF)是一种能有效消除由非线性负载产生的谐波电流的电力装置［1］.APF的控制系统可以使实际输出补偿电流实时跟随指令电流的变化［2］.APF预测电流控制方法通过在第k采样时刻预测第k+1时刻的APF参考电流.预测电流的方法有:人工神经网络预测［3］、拉格朗日外推插值算法［4］和线性预测方法［5］，前者计算量大，后两者准确度不高.本研究将改进的带有收敛因子的粒子群算法应用于预测电流控制中，通过仿真分析，输出预测电流的准确度得到进一步提高，补偿后系统线路中电流的畸变率减小，且计算量较小，暂态响应过程平稳，在谐波指令电流突变点附近误差较小，提高了APF的谐波补偿效果.

1 有源电力滤波器的预测控制

建立APF数学模型.在图1中，忽略APF交流侧电阻的影响，可以得出下列关系式:

对式(1)进行离散化处理可得:

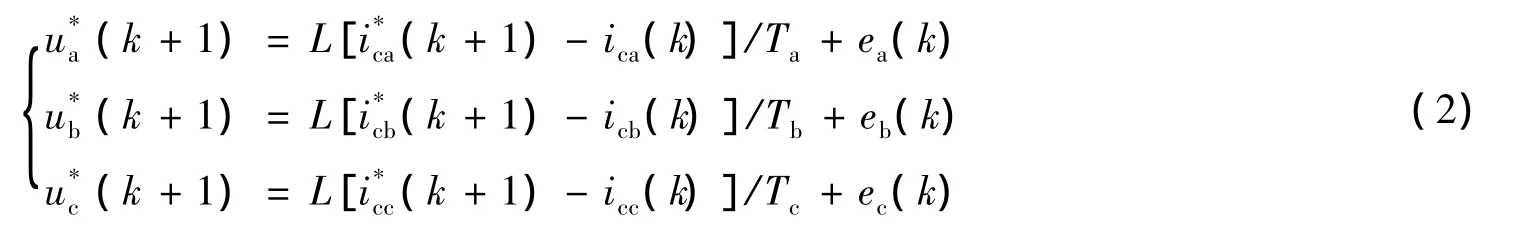
(2)式中:(k+1)和(k+1)分别为在k+1采样时刻APF的指令电流与参考电压，T为系统采样周期.

由式(2)可知，为了在k采样时刻得到k+1时刻的APF参考电压(k+1)，就必须提前一个采样时刻预测出APF的指令电流(k+1)，应用(k+1)和(k+1)值再通过相应的控制算法可得到合适的APF开关控制信号，从而达到电流跟踪控制的目的［4－6］.

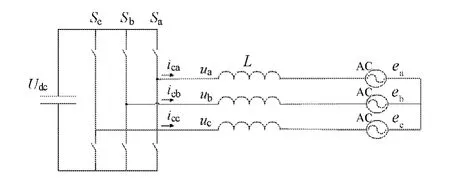
图1 并联APF等值电路Fig.1 Equivalent circuit of the SAPF

2 指令电流的预测策略

要实现APF预测电流控制的功能，在当前采样时刻能准确、快速地预测下一采样时刻的指令电流值是非常重要的［7－11］.

采用快速预测指令电流的策略如图2所示.

首先，根据式(3)的条件，判断系统的不确定性以及外界的各种干扰的状况，

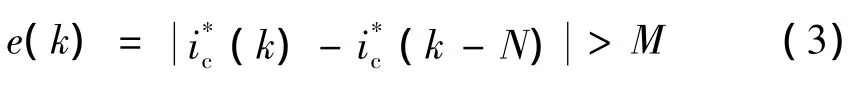
其中:M定义为常数，本文设定为0.1;N为一个周期的采样点数.

当式(3)不成立时，可以认为负载电流及其所含有的谐波电流成分都比较稳定，指令电流可以近似认为是周期变化的，因此可以利用上一周期的历史数据来产生下一采样时刻的指令电流预测值(k+1)，即:

当式(3)成立时，说明电流发生较大的变化，将采用拉格朗日插值法做外推预测来得到下一采样时刻的指令电流预测值，(k+1)为:

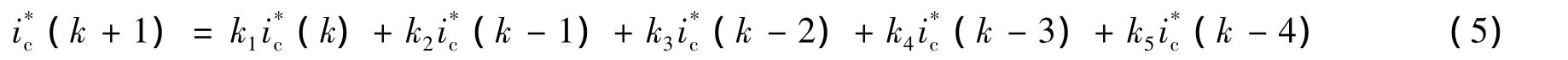
其中:k1、k2、k3、k4和k5为拉格朗日的插值系数.

3 基于改进的带有收敛因子的粒子群算法预测电流控制的参数优化

在电流预测策略中，式(5)中拉格朗日的插值系数以及对应的线性插值系数的选取将直接影响电流预测的准确性.选取k+1时刻之前的5个采样点对k+1时刻的电流值进行预测，分别赋予相应的5个参数，并对其参数进行优化.对带有收敛因子的粒子群算法进行改进，优化其局部搜索能力，并将其应用于APF电流预测策略的参数优化.

在每一次迭代中，粒子跟踪其本身个体极值点(pbest)，以及整个种群中所找到的最好解即全局极值点(gbest).在找到这两个极值点后，粒子根据式(6)、(7)和(8)来分别更新算法的速度v、收敛因子β和位置x.

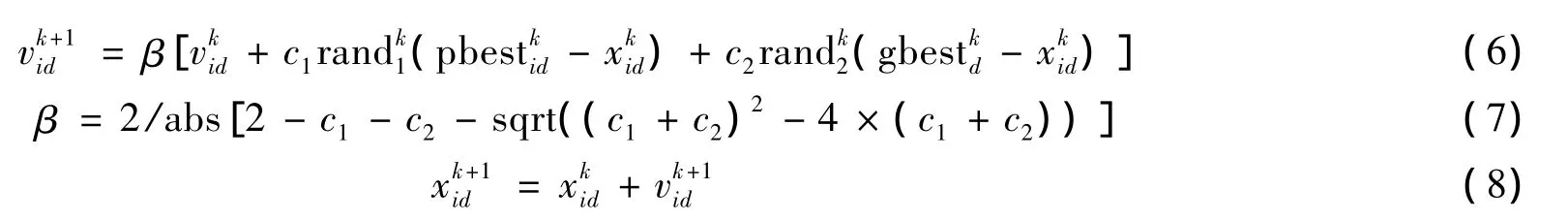
其中:v是粒子i在第k次迭代中第d维的速度;c1、c2是加速系数(或称学习因子)，合适的c1、c2可以加快收敛且不易陷入局部最优;rand1、2是［0，1］之间的随机数;x是粒子i第k次迭代中第d维的当前位置;pbestid是粒子i在第d维的个体极值点的位置(坐标);gbestd是整个群体在第d维的全局极值点的位置［12－16］.

对预测电流控制中的系数进行PSO参数寻优时，选取个体最优适应函数值fbest(m)为:

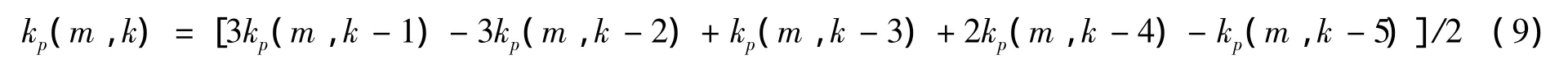
上式中，p=1、2、3、4、5，

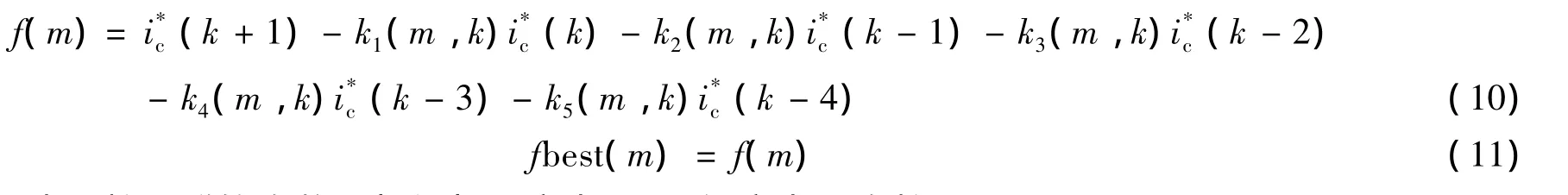
其中:m表示表示粒子群的个数，本文中m定为6，即设定为6个粒子;k1(m，k)、k2(m，k)、k3(m，k)、k4(m，k)和k5(m，k)分别是寻优的5个参数;fbest(m)表示个体最优适应度函数值，即每个粒子每次迭代得到的最优参数，然后判定参数值与其相对应的电流值乘积和能否正确计算下一时刻预测的电流值.

结合式(6)至式(8)，进行粒子群粒子的位置与速度更新.结合式(9)至式(11)，可求取f(m)的最小值，通过求取全局最优适应函数值即fgbest=min(fpbest)，其中pbest表示每次迭代中所有粒子得到全局最优的粒子位置即5个采样时刻电流值对应的系数值，得到全局最优的位置，进而确定预测电流控制中的5个参数的值.

式(9)中体现了对收缩因子法的改进，对每一个粒子在经过一次迭代后生成的满足个体最优适应度函数值的最后5个最优位置同时进行拉格朗日插值与线性插值运算，然后将两次插值的结果取平均值，得出一次迭代后的个体最优位置，最后通过群体适应度函数条件的判别，得出pbest的值即群体最优值.因为拉格朗日插值比线性插值算法有更强的局部搜索能力，在接近最小值附近做二次插值会比在其他位置做二次插值来的精确［17］.将带有收敛因子的粒子群算法在每一个粒子经过一次迭代运算后的最后5个数值做插值运算，可以帮助算法本身提高粒子群运算的精度，同时将插值法与粒子群的收缩因子法相结合，提高了算法的局部搜索能力.

4 仿真实验

粒子群数目为30个，参数个数设定为5个，迭代次数为500次，算法中参数的含义同上一节.应用改进的收敛因子法PSO进行参数寻优，得出优化后的5个采样时刻电流的插值系数为3、－3、0.5、0.5、0，即全局最优位置.将以上5个系数代入Simulink仿真模型中，进行在线仿真.

通过Simulink对构建的APF模型进行仿真，APF模型如图3所示.

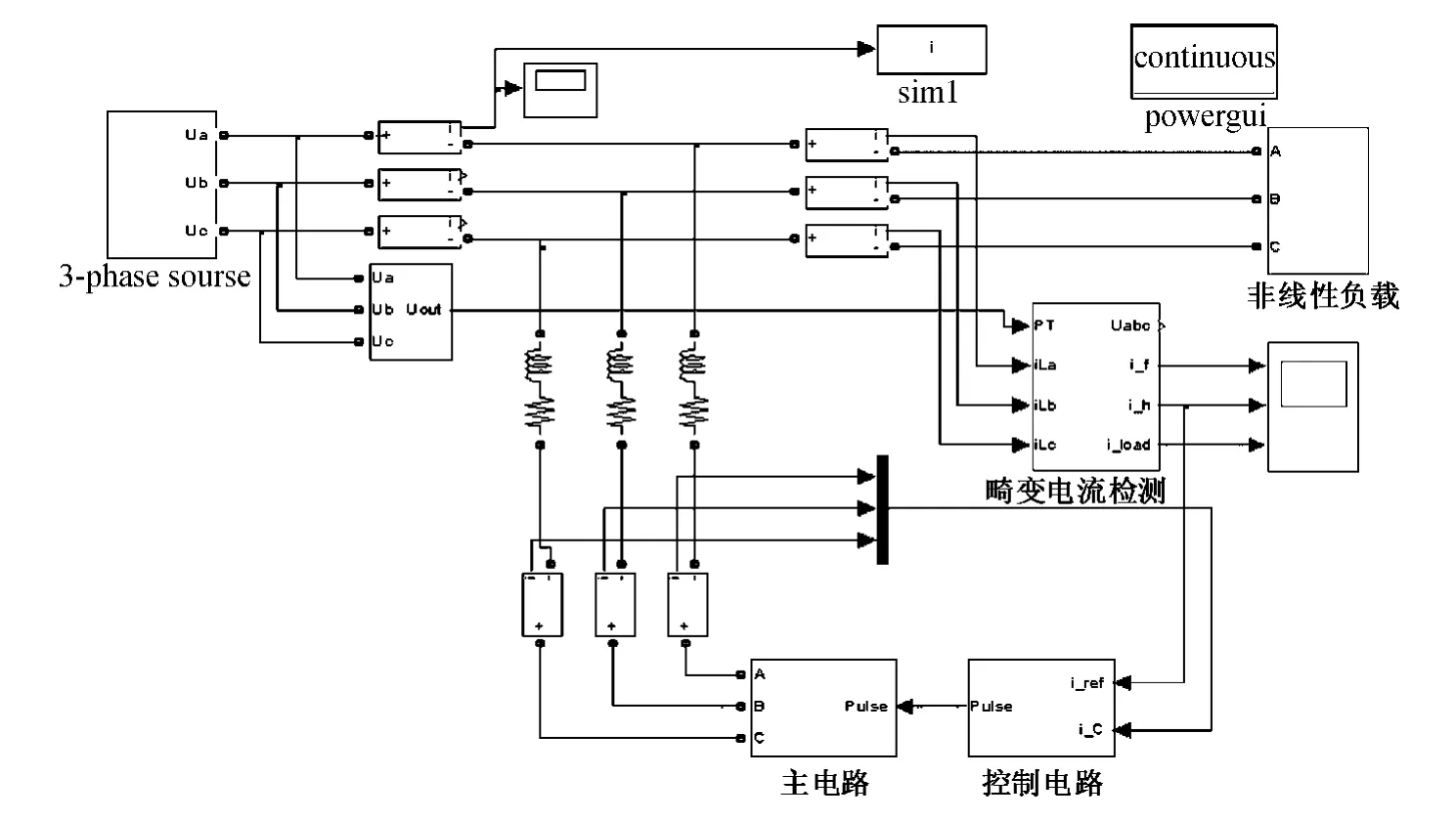
图3 APF模型Fig.3 Model of APF

负载谐波电流的次数主要包含有5次、7次和11次谐波，谐波的傅里叶分析如图4所示，其中APF输出的实际谐波指令电流如图5所示.采用基于改进粒子群算法的预测电流控制，算法输出的指令电流波形如图6所示.

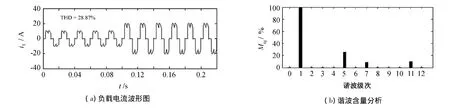
图4 未补偿系统线路的电流Fig.4 Uncompensated current of the power system

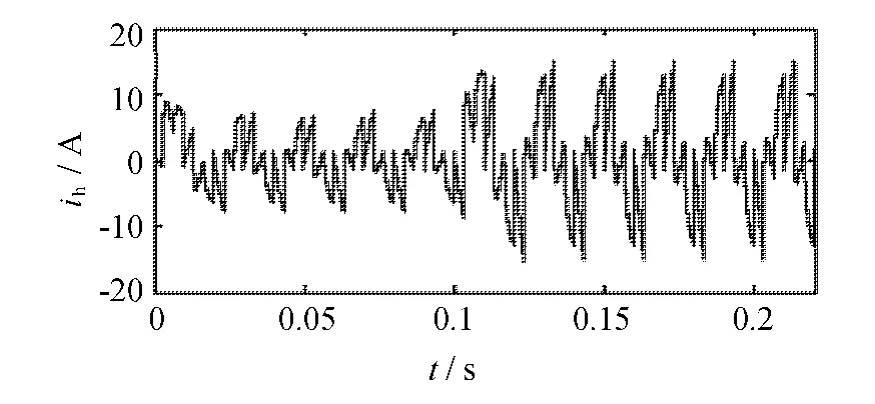
图5 实际指令电流波形Fig.5 Waveform of the actual current

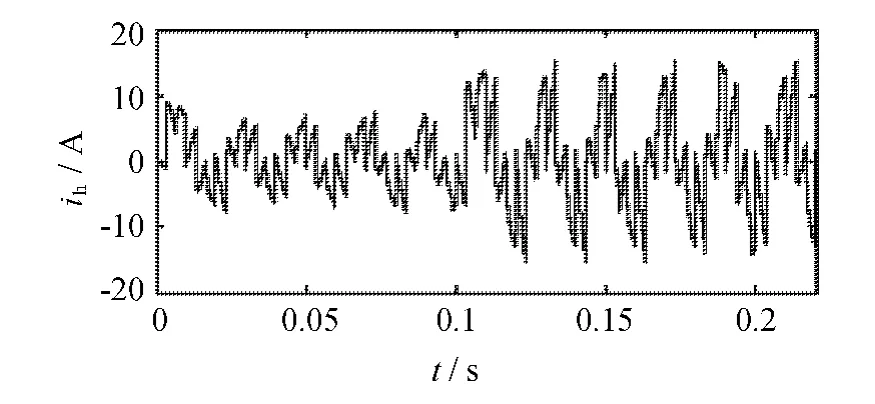
图6 预测指令电流波形Fig.6 Waveform of the predictive instruction current

为了便于对该算法的预测精度进行分析，将实验得到的预测指令电流与实际指令电流之间的误差进行积分.采用插值系数为3，－3，1，0，0时所得到的预测指令电流与实际指令电流之间的误差进行积分［4］.所得预测指令电流的误差积分曲线如图7(a)所示.

图7(a)中，曲线2是本文预测算法得出的预测指令电流误差积分曲线，曲线1是拉格朗日插值系数为3，－3，1，0，0时的预测指令电流误差积分曲线.对比实验结果可以看出，经过改进型PSO参数优化算法得出的插值系数值，其预测指令电流值与实际指令电流值的差值比未优化的差值小，表明插值系数优化后的预测指令电流更接近真实的指令电流值，准确度更高.

再将该预测算法的实验结果与采用线性插值法做外推预测指令电流所得到的误差积分曲线［6］进行比较，得出的预测指令电流的误差积分曲线分别如图7(b)所示.其中，曲线2是本文预测算法实验得到的指令电流误差积分曲线，曲线1是采用线性插值法做外推的预测指令电流误差积分曲线，对比之下也能得到上述同样的结论.

为了验证预测电流控制在APF负载发生突变时的动态补偿效果，假设在仿真时间为0.1s时，APF系统中负载突然减半，对模型中补偿后系统线路中的动态电流进行傅里叶分析.

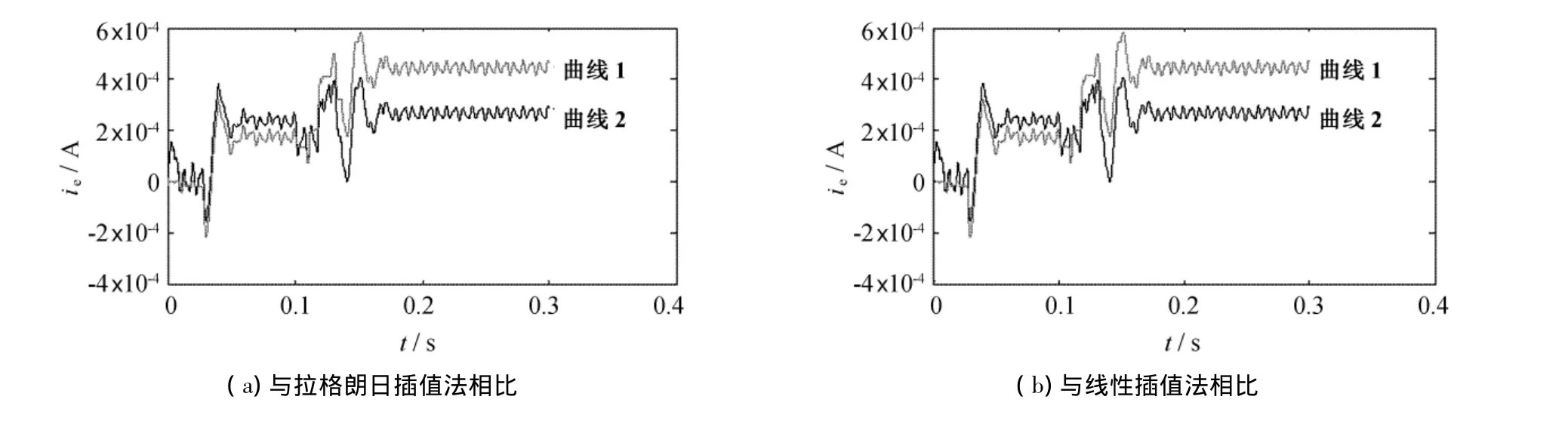
图7 不同方法的误差积分曲线Fig.7 Curves of the predictive instruction current

图8是采用文献［4］拉格朗日插值外推算法的预测电流控制的实验结果.可以看出，经过APF补偿后大大减小了电流的畸变率.但是，当负载发生突变，由于预测指令输出的电流值不稳定，使得系统线路中的电流发生振荡，控制的稳定性下降，预测指令电流与实际电流之间存在较大的误差.

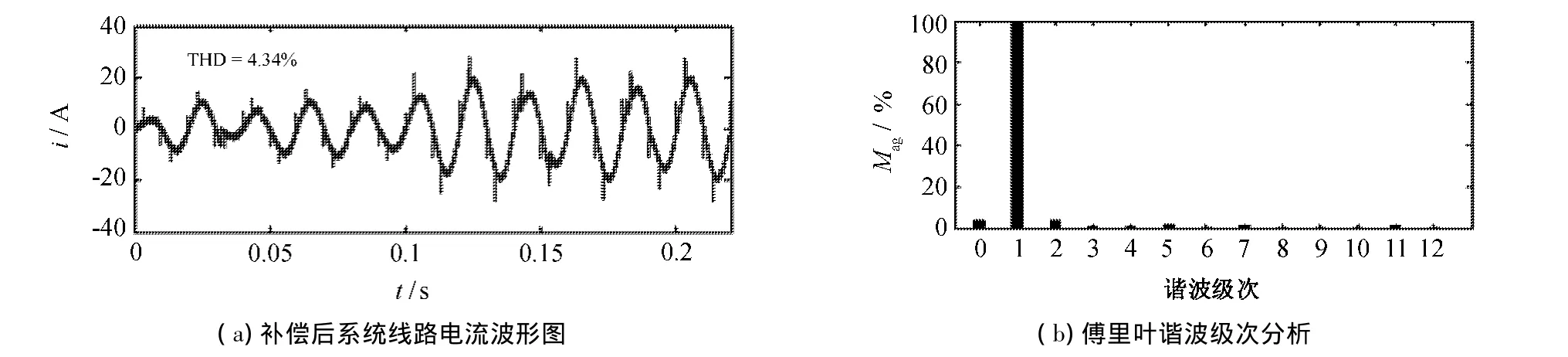
图8 拉格朗日插值后的系统线路电流傅里叶分析Fig.8 The Fourier analysis of the current of power system after the Lagrange＇s interpolation

采用文献［6］线性插值外推算法和本文中所述基于改进粒子群算法的预测电流控制，对补偿后线路中的电流进行傅里叶分析，分别如图9和图10所示.

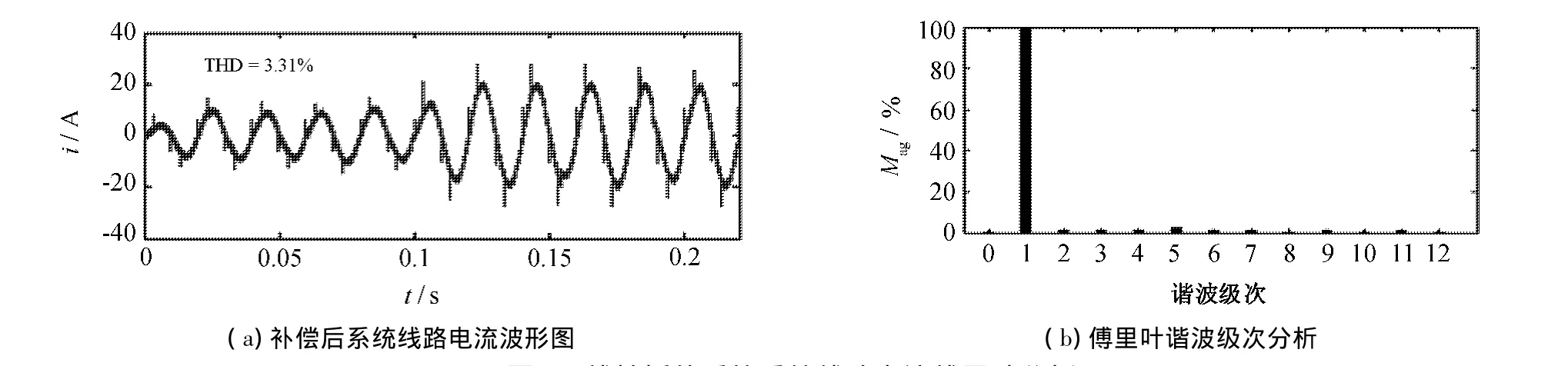
图9 线性插值后的系统线路电流傅里叶分析Fig.9 The Fourier analysis of the current of power system after the linear interpolation

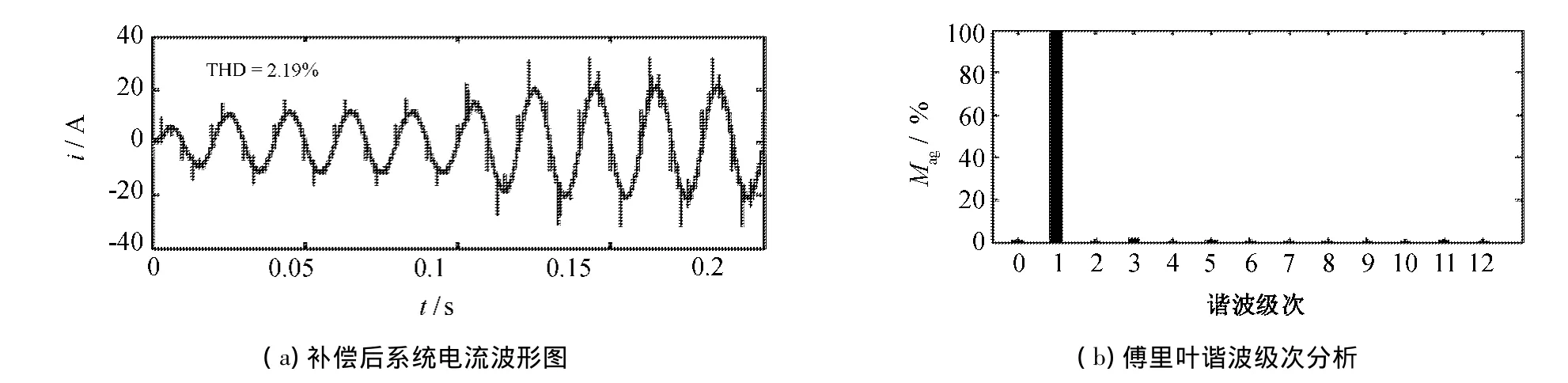
图10 参数优化后的系统线路电流傅里叶分析Fig.10 The Fourier analysis of the current of power system after the parameter optimization

从图10可以看出当负载发生突变，经过参数优化以后的预测指令输出的电流不会造成系统线路中电流的振荡，补偿后系统稳定性较好，预测指令电流与实际电流的误差较小.

三种方法仿真试验对比的结果见表1.从实验对比结果可以看出，采用基于改进粒子群算法的预测电流控制所得到的预测指令电流更接近真实的指令电流值，准确度更高.APF补偿后线路中电流的畸变率明显减小，提高了APF的谐波补偿效果.

表1 预测指令电流三种方法对比Tab.1 The comparisons of the three methods of predictive instruction current

5 结语

利用改进的带有收敛因子的粒子群算法对预测电流控制中的参数进行优化.改进后的带有收敛因子的PSO算法相较于未改进的带有收敛因子的PSO算法，其局部探索能力得到加强，不易陷入局部最优.通过对优化后的系数以及仿真实验结果进行分析，说明该方法进一步提高系统输出谐波预测指令电流的准确度，电流暂态响应过程较为平稳，在谐波指令电流突变点附近误差较小，减小补偿后系统线路中电流的畸变率，使得APF的谐波补偿效果得到提高.

［1］姜齐荣，赵东元，陈建业.有源电力滤波器:结构·原理·控制［M］.北京:科学出版社，2005.

［2］Han B M，Bae B Y，Ovaska S J.Reference signal generator for active power filters using improved adaptive predictive filter［J］.IEEE Transaction on Industrial Electronics，2005，52(2):576－584.

［3］颜文旭，韩立圣，惠晶，等.三相四线有源电力滤波器新型神经预测控制［J］.电力系统及其自动化学报，2011，23(1):28－33.

［4］郭自勇.有源电力滤波器检测与控制技术的研究及应用［D］.长沙:湖南大学，2007.

［5］周宏斌.基于无差拍控制策略的并联有源电力滤波器研究［D］.南宁:广西大学，2009.

［6］何英杰，刘进军，王兆安，等.基于重复预测原理的三电平APF无差拍控制方法［J］.电工技术学报，2010，25(2):114－120.

［7］Kouro S，Cortes P，Vargas R，et al.Model predictive control－ a simple and powerful method to control power converters［J］.IEEE Transactions on Industrial Electronics，2009，56(6):1 826－1 838.

［8］Correa P，Rodriguez J，Rivera M，et al.Predictive control of an indirect matrix converter［J］.IEEE Transactions on Industrial Electronics，2009，56(6):1 847－1 853.

［9］Cortes P，Ortiz G，Yuz J I，et al.Model predictive control of an inverter with output LC filter for UPS application［J］.IEEE Transactions on Industrial Electronics，2009，56(6):1 875－1 883.

［10］Miranda H，Cortes P，Yuz J I，et al.Predictive torque control of induction machines based on stat－ space models［J］.IEEE Transactions on Industrial Electronics，2009，56(6):1 916 －1 924.

［11］Vargas R，Ammann U，Rodriguez J.Predictive approach to increase efficiency and reduce switching losses on matrix converters［J］.IEEE Transactions on Power Electronics，2009，24(4):894 －902.

［12］温惠英，李俊辉，周玮明.适于车辆路径规划的改进型粒子群优化算法［J］.华南理工大学学报:自然科学版，2009，37(7):1－5.

［13］何潜，王岗，雷雨，等.基于改进粒子群优化算法的火电机组负荷多目标优化［J］.电网技术，2010，34(8):118－122.

［14］顾威，李兴源，王渝红，等.基于改进粒子群算法的次同步阻尼控制器设计［J］.电网技术，2010，34(8):52－56.

［15］吴昌友，王福林，董志贵，等.改进粒子群优化算法在电力负荷组合预测模型中的应用［J］.电网技术，2009，33(2):27－30.

［16］陈如清.采用新型粒子群算法的电力电子装置在线故障诊断方法［J］.中国电机工程学报，2008，28(24):70－74.

［17］莫祯贞.改进粒子群算法在模糊环境下平行机批调度问题中的应用研究［D］.合肥:中国科学技术大学，2010.