周期性边界条件下炭黑增强橡胶基复合材料有效弹性性能数值模拟

李庆，杨晓翔

(福州大学机械工程及自动化学院，福建福州 350116)

0 引言

橡胶是一种无定形的高聚物，又可称为弹性体.橡胶具有优异的弹性、良好的柔软性，较高的耐磨性、电绝缘性、致密性以及耐腐蚀、耐溶剂、耐高低温等特殊性能，广泛应用于能源建设、交通运输、土木建筑、医疗卫生、军事国防以及航天、航空、宇宙开发等多个领域.虽然橡胶具有优良的特性，但是单用生胶(包括天然橡胶及合成橡胶)并不能制得符合各种使用要求的橡胶制品.工业上使用的橡胶材料都是由本体材料和各种配合剂构成的细观复合材料，其中炭黑填料粒子是橡胶工业中最重要的补强剂，它能提高橡胶的模量、拉伸强度、撕裂强度、耐磨性、扯断伸长率及黏度等，会降低压缩永久变形和口型膨胀等性能，所以，炭黑的填充明显改善了橡胶的静态与动态性能［1］.

炭黑填料对改善橡胶材料的力学性能起着至关重要的作用，它对橡胶性能的影响主要取决于填料的粒径、含量、形态结构和表面性质等结构因素［2］，所以，为指导相关材料设计，缩短研发周期，必须建立炭黑颗粒填充橡胶复合材料的细观结构与宏观性能的内在联系和规律的定量关系.对此，Govindjee［3］，Bergstrom＆Boyce［4］以及夏勇［5］等国内外很多学者进行了探索研究，并建立多种细观数值模型对炭黑填充橡胶进行力学行为分析，主要有单颗粒夹杂二维平面应力模型和三维轴对称模型，多颗粒夹杂二维平面应力模型以及采用若干个相同的菱形十二面体建立的三维数值模型.就炭黑填充橡胶复合材料细观数值模型的发展而言，目前仅处在初步阶段，实际考察的因素仅有体积分数一种，仍有许多不完善之处.

本研究基于细观结构的周期性假设，建立联系复合材料宏观和细观特征的细观数值模型，对炭黑填充橡胶复合材料进行单向拉伸的数值模拟，比较分析圆形和方形炭黑填料粒子模型的变形场和应力场，以及炭黑填料的含量对于复合材料有效弹性模量的影响规律.

1 复合材料细观力学研究基础

1.1 代表性体积单元

如图1所示，对于颗粒增强型复合材料通常假定宏观材料具有周期性的细观结构，即采用代表性体积单元(RVE)进行细观力学研究，图1(b)为单颗粒夹杂RVE示意图，图1(c)为多颗粒夹杂RVE示意图.对于RVE的选取，它应该选取足够大以包含充分的细观结构组成信息，而同时RVE的尺寸又要足够小以反映其细观非均质性［6－7］.

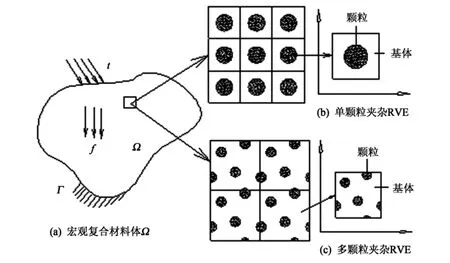
图1 RVE选取示意图Fig.1 Extracting diagram of RVE

1.2 周期性边界条件

代表性体积单元是宏观复合材料连续统一体的代表，需要在邻近代表性体积单元的边界施加周期性边界条件［5，8－9］以确保变形场的协调性，主要包括位移连续条件和应力连续条件.

1.2.1 位移连续条件:RVE对边边界形状保持相同

图2所示为二维代表性体积单元的几何表述，其外框为一边长为L的正方形，顶点A0为坐标原点，顶点A1和A2分别位于坐标轴x和y上，则对边边界上点的自由度应满足以下约束关系:

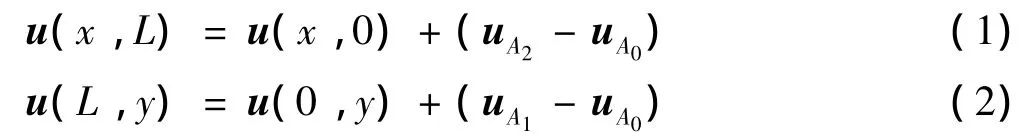
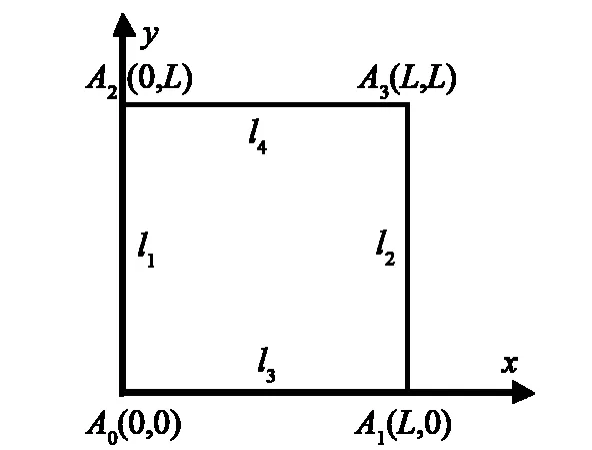
图2 二维RVE的几何表述Fig.2 Geometrical frame of two －dimensional RVE

式中:uAi代表顶点Ai的位移矢量，i=0，1，2.若分别用l1、l2、l3、l4代表RVE中x=0、x=L、y=0、y=L时的边界，用uli代表RVE边界li上点的位移矢量，则约束方程(1)和(2)可写为:

则RVE边界l2和l4上的节点(不包含顶点)称为被约束节点，而边界l1和l3上的节点称为保留节点，被约束节点的位置由保留节点的位置来确定.

由边界虚位移引起的虚应变能变化为:

式中:σl代表RVE边界的柯西应力张量，nl代表其外法线单位向量.由lRVE=l1+l2+l3+l4，则式(5)可展开为:

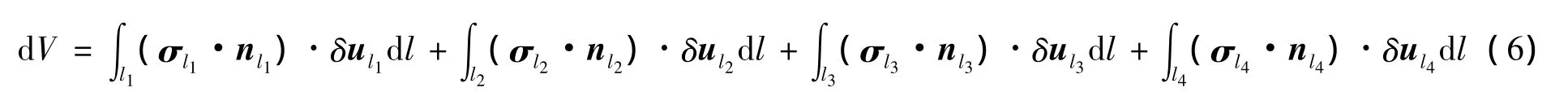
把位移约束方程式(3)和式(4)代入式(6)，可得:

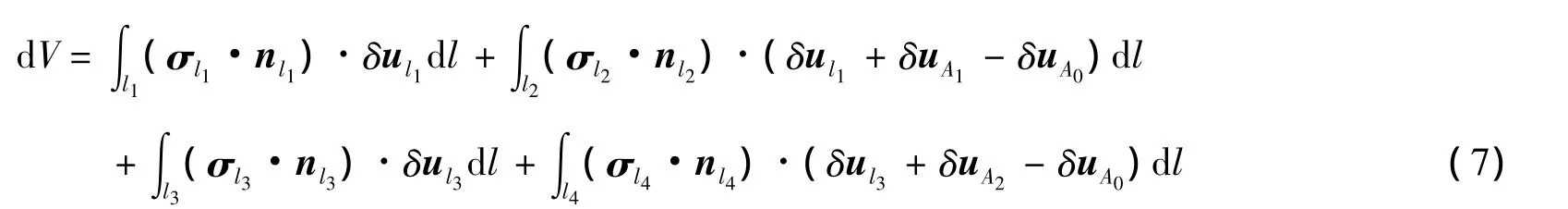
因为RVE对边边界形状相同，l1=l2，l3=l4，则式(7)可写为:

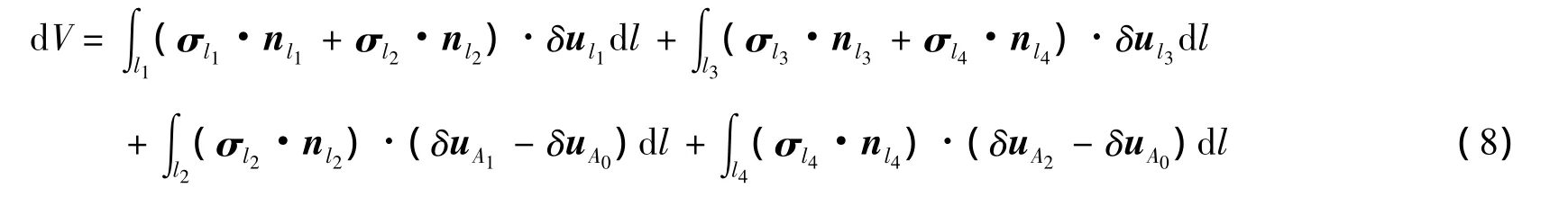
根据变形体的虚功原理，外力在虚位移上所做的外力虚功dW恒等于内应力在虚应变上所做的虚变形功(即虚应变能变化dV)，则有:

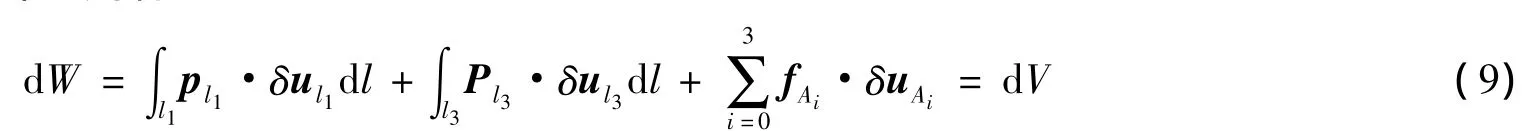
式中:Pli代表外部作用于RVE边界li上的分布载荷，fAi代表外部作用于RVE顶点Ai上的集中载荷.根据式(8)和式(9)，可得出外部载荷表达式为:

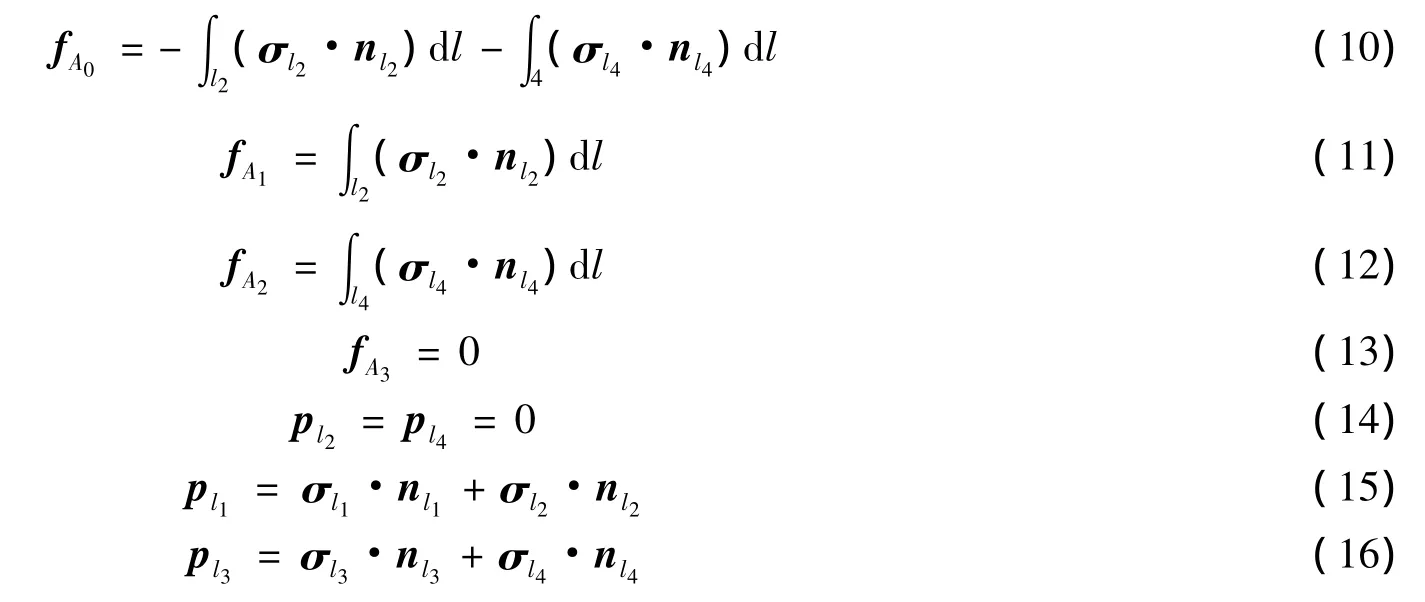
1.2.2 应力连续条件:RVE对边边界上应力矢量大小相等，方向相反

对边边界上点的应力应满足以下约束关系:

将式(17)和式(18)分别代入到式(15)和式(16)，可得:

由以上推导可得，周期性边界条件约束的结果不仅使被约束节点的位置可以由保留节点的位置来确定，还使RVE所受的外部载荷可以由分配到顶点上的集中载荷来等效，因此，具有周期性的二维RVE模型的外加载荷仅仅需要作用于顶点A0，A1和A2上.

2 有限元建模

形如图1(b)所示的单颗粒夹杂代表性体积单元只适用于研究颗粒分布均匀的填充复合材料，对于颗粒随机分布的复合材料，单颗粒夹杂RVE已经不再适用，必须建立符合颗粒随机分布真实情况的RVE.所以，本研究采用多颗粒夹杂的代表性体积单元，如图1(c)所示，考虑复合材料中颗粒随机分布特征，通过建立具有随机分布形态的代表性体积单元的数值模型，来模拟分析炭黑颗粒填充橡胶复合材料的力学行为.

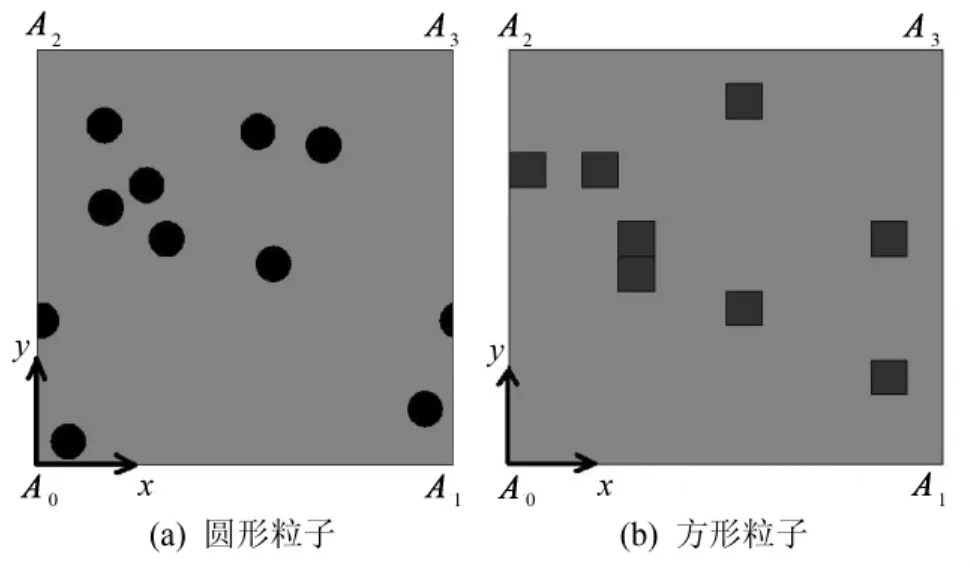
图3 RVE模型Fig.3 RVE model

对于多颗粒夹杂随机分布的二维代表性体积单元建模时，将橡胶基体和炭黑粒子之间的界面假设为理想连接状态，不发生脱落现象［4］.如图3所示，采用RSA算法［10］通过MATLAB随机函数程序在给定区间［0，L］产生两个均匀分布的伪随机数，用来确定颗粒形心的位置坐标，分别建立圆形粒子和方形粒子的RVE模型，RVE边长均为L=24 μm.其中，圆形颗粒半径为r=1 μm，颗粒个数m=10，颗粒所占体积分数φr=5.45%;方形颗粒边长为b=2 μm，颗粒个数n=8，颗粒所占体积分数φb=5.56%.

模型中炭黑颗粒看作为线性弹性材料，弹性模量Ef=200 MPa，泊松比设为 υf=0.3［4］.

橡胶基体本构关系采用近乎不可压缩的Mooney－Rivlin模型［11－12］

其中:C10和C01是同温度有关的材料常数，与初始剪切模量μ0的关系为［12－13］:

设初始弹性模量Em=2 MPa，泊松比υm=0.5，则有初始弹性模量与剪切模量关系式［12］

根据式(21)和式(22)，并取材料常数C10与C01的比值为4［13］，可计算得到Mooney－Rivlin模型中的材料常数C10=0.266 7 MPa，C01=0.066 7 MPa.

在Abaqus/Standard中进行网格划分时，橡胶基体采用平面应变8节点四边形二次完全积分的杂交单元CPE8H①ABAQUS Inc.ABAQUS analysis user’s manual.The State of Rhode Island and Providence Plantations:ABAQUS Inc，1978.，炭黑颗粒采用CPE8.特别提出的是，要保证模型对边网格相同，节点一一对应，以便于施加周期性边界条件的约束方程.在ABAQUS软件中，通过添加约束方程*Equation来实现方程式(1)和方程式(2)所描述的约束.为给定RVE有限元模型充分的约束，还需要约束顶点A0在x、y方向的位移，约束顶点A1在y方向的位移，约束顶点A2在x方向的位移.然后通过在顶点A1施加x方向位移载荷进行单轴拉伸的模拟.

3 结果与讨论

3.1 变形场和应力场分析

基于本研究提出的方法和参数对图3所示的几何模型沿x方向施加拉伸位移载荷，对RVE施加周期性边界条件约束后进行有限元计算.图4给出了拉伸位移为15 μm时的变形图，从图4中可以看出橡胶基体产生的变形较大，而炭黑颗粒基本上没有变形.通过分析发现RVE对边边界的形状在变形过程中始终保持完全相同，符合周期性结构位移连续的真实情况.

图5给出了拉伸位移为15 μm时的von－Mises应力等值线图，并且沿x和y方向分别周期排列2个.从两幅图中可以看出模型中应力分布并不均匀，距离填充颗粒越近的橡胶基体处等值线越密集，应力梯度越大;距离填充颗粒越远的橡胶基体处等值线越稀疏，应力梯度越小.将方形粒子与圆形粒子模型的应力等值线图相比较可以看出，在相同的载荷条件下，方形粒子模型中的应力集中现象更加明显，应力值相对更高，如图5所示，方形粒子模型中最大应力值为29.996 MPa，而圆形粒子模型中的最大应力值只有5.066 MPa.分别观察两幅图中相邻RVE共同边界处的应力等值线分布情况，发现它们在加载过程中始终构成连续闭合曲线，RVE中对边边界的应力等值线分布相同，满足RVE对应边界的对应节点应力一致条件，符合周期性结构应力连续的真实情况.

图4 RVE的变形图Fig.4 Deformation of RVE

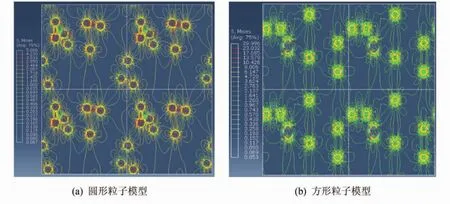
图5 RVE的von－Mises应力等值线图Fig.5 The distribution of von － Mises stress in RVE

图6给出了圆形和方形粒子模型的平均应力－应变曲线，其中，复合材料的真实应力(MPa)由加载方向的约束反力除以变形后的表面积得到;真实应变由如下公式得到:

式中:u为加载的位移(μm)，L为RVE边长(μm).

从图6中可以看出应力与应变呈非线性关系，符合橡胶材料的非线性弹性的特性.所以，本文研究所建立的模型可以用来模拟炭黑填充橡胶复合材料的力学行为.

3.2 炭黑颗粒含量和形状对复合材料有效弹性模量的影响

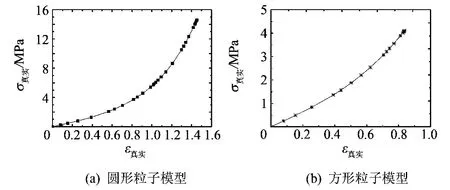
图6 RVE的平均应力－应变曲线Fig.6 The stress－ strain behavior of RVE

基于本研究提出的方法和参数，保持炭黑颗粒大小不变，增加颗粒数目，分别建立不同炭黑体积含量的代表性体积单元，通过平面应变模型进行单轴拉伸的有限元模拟，计算橡胶复合材料在不同炭黑含量下的平均应力－应变曲线，如图7所示.

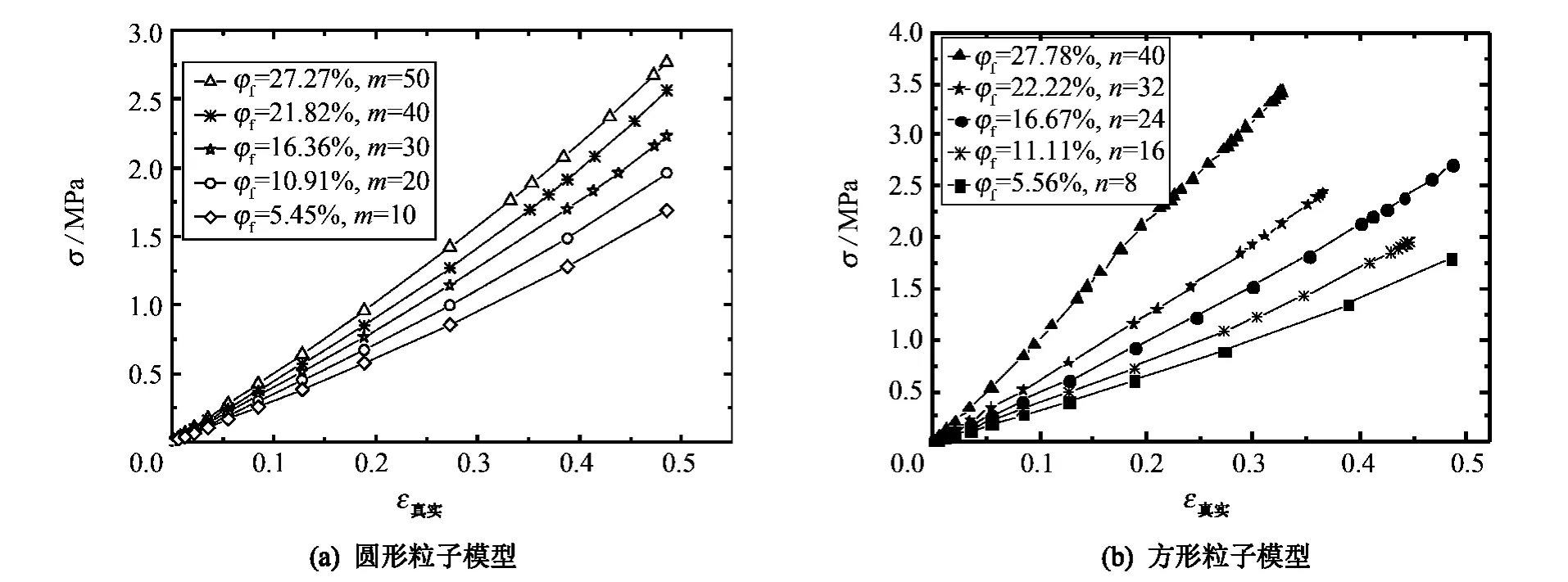
图7 不同颗粒体积分数下的复合材料应力－应变关系曲线Fig.7 Influence of volume fraction of particles on the stress－ strain behavior

采用应力－应变曲线在真应变为0.002处的正割模量来近似炭黑填充橡胶材料的有效弹性模量＜E＞［4］，即

其中:ε=0.002，σ为应力－应变曲线上ε=0.002时的应力值(MPa)，所以，有效弹性模量＜E＞的单位也为MPa.由此方法，可以得到不同颗粒含量下的炭黑填充橡胶材料的有效弹性模量＜E＞，如图8所示.同时，图8还给出了Bergstrom＆Boyce通过实验得到的7%、15%和25%炭黑N600填充氯丁橡胶的有效弹性模量的实验结果.将圆形粒子和方形粒子的有限元模型对不同含量炭黑填充的橡胶复合材料有效弹性模量的预测结果与实验结果进行比较分析，发现它们所呈现的趋势一致.即，炭黑颗粒的填充使得橡胶材料的弹性模量明显增大，炭黑填充橡胶材料的有效弹性模量随着炭黑颗粒所占体积分数的增加而增大;表明本研究基于周期性边界条件所建立的二维多颗粒夹杂RVE模型是合理的，能够用于炭黑颗粒增强橡胶基复合材料有效性能的模拟分析.另外，从图8中还可以看出，在相同的炭黑填料体积分数下，方形粒子模型对炭黑填充橡胶材料的有效弹性模量的预测结果明显高于圆形粒子模型.

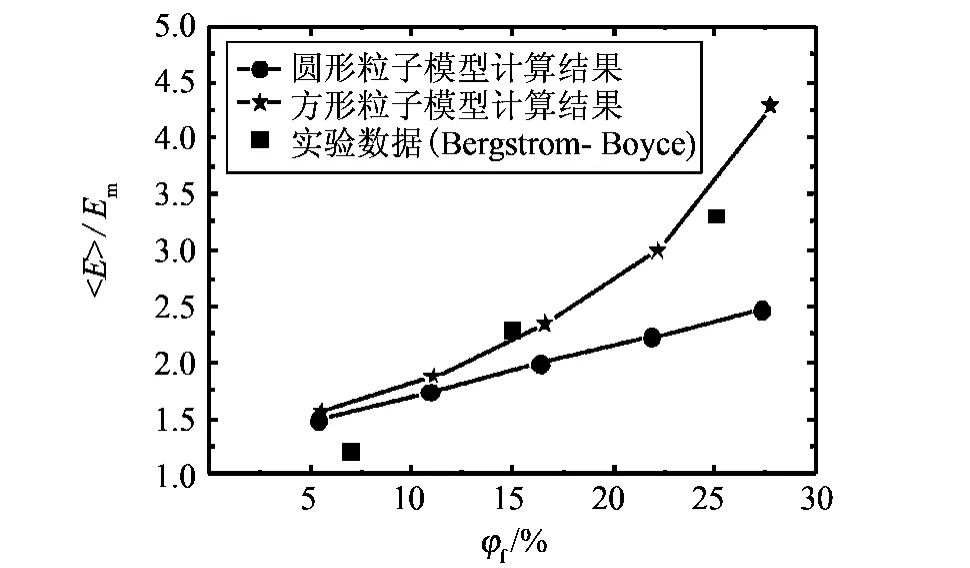
图8 不同炭黑颗粒含量下橡胶复合材料的有效弹性模量Fig.8 Influence of volume fraction of particles on the normalized Young’s modulus

4 结语

通过建立具有随机分布形态的代表性体积单元的二维数值模型，对炭黑颗粒填充橡胶复合材料的力学行为进行非线性有限元分析.研究表明，该方法通过周期性边界条件的约束使得模型在整个加载过程符合周期性结构的位移连续和应力连续的真实情况，保证了变形场的协调性，可较好地模拟颗粒增强橡胶基复合材料的等效力学性能.结果显示:

1)炭黑的填充明显增大了橡胶材料的弹性模量;

2)炭黑填充橡胶材料的有效弹性模量随着炭黑颗粒所占体积分数的增加而增大;

3)在相同的炭黑填料体积分数下，方形粒子模型对炭黑填充橡胶材料有效弹性模量的预测结果明显高于圆形粒子模型;

4)本研究中圆形粒子和方形粒子的有限元模型对不同含量的炭黑填充橡胶材料有效弹性模量的预测结果与实验结果吻合较好，证实了本研究基于周期性边界条件所建立的二维多颗粒夹杂RVE模型是合理的，为炭黑颗粒增强橡胶基复合材料其他性能的分析提供了依据.

［1］王艳秋.橡胶材料基础［M］.北京:化学工业出版社，2006.

［2］傅政.橡胶材料性能与设计应用［M］.北京:化学工业出版社，2003.

［3］Govindjee S.An evaluation of strain amplification concepts via Monte Carlo simulations of an ideal composite［J］.Rubber Chemistry and Technology，1997，70:25－37.

［4］Bergstrom J S，Boyce M C.Mechanical behavior of particle filled elastomers［J］.Rubber Chemistry and Technology，1999，72:633－656.

［5］夏勇.轮胎胶料在较大变形范围内准静态力学性能的研究——测试、表征以及细观数值本构模型［D］.合肥:中国科学技术大学，2004.

［6］Gitman I M，Askes H，Sluys L J.Representative volume:existence and size determination［J］.Engineering Fracture Mechanics，2007，74:2 518 －2 534.

［7］Hassani B，Hinton E.A review of homogenization and topology optimization II－analytical and numerical solution of homogenization equations［J］.Computers and Structures，1998，69:719 － 738.

［8］Smit R J M，Brekelmans W A M，Meijer H E H.Prediction of the mechanical behavior of nonlinear heterogeneous systems by multi－ level finite element modeling［J］.Computer Methods in Applied Mechanics and Engineering，1998，155:181 －192.

［9］Smit R J M，Brekelmans W A M，Meijer H E H.Prediction of the large－strain mechanical response of heterogeneous polymer systems:local and global deformation behavior of a representative volume element of voided polycarbonate［J］.Journal of the Mechanics and Physics of Solids，1999，47:201 －221.

［10］Segurado J，Llorca J.A numerical approximation to the elastic properties of sphere － reinforced composites［J］.Journal of the Mechanics and Physics of Solids，2002，50:2 107 －2 121.

［11］Boyce M C，Arruda E M.Constitutive models of rubber elasticity:a review［J］.Rubber Chemistry and Technology，2000，73(3):504－552.

［12］张少实，庄茁.复合材料与粘弹性力学［M］.北京:机械工业出版社，2005.

［13］Gent A N.Engineering with rubber:how to design rubber components［M］.Lübeck:Hanser Gardner Publications，2001.