规划高速公路路线的变异蚁群算法

尚艳艳，李应，董晨

(福州大学数学与计算机科学学院网络系统信息安全福建省高校重点实验室，福建福州 350116)

1 路径规划问题

路径规划是指在数据或物理网络中选择路径的过程.机器人路径规划［1－4］和物流配送路径优化［5－6］是常见的路径规划的问题，也是采用蚁群算法研究的两个热点.蚁群算法是信息正反馈原理和启发式算法的有机结合，在求解组合优化等问题方面具有其它群智能算法所不具有的优点［7］.正反馈原理虽然可以强化较优的解，却容易陷入停滞现象，所以在采用蚁群算法规划路径时往往对蚁群算法做一些改进.规划高速公路修建路线和机器人寻径相同的是给出起点和终点，搜索一条最优路径.但不同的是，机器人遇到障碍物时选择绕开［1－4］，而修建高速公路时可以通过架设高架桥、开凿隧道等手段通过河流、高山等障碍物.

1.1 地理信息表示

修建高速公路的区域可能有高山、山谷、河流和城镇等地理情况，为了更好地研究路径规划问题，需要较准确地表示该路径规划区域的地理信息.

地图和路径有坐标、网格和位图三种地图表示方法.坐标地图最贴近实际，但其坐标值是浮点数，蚂蚁的行动方向没有限制，导致对路径的保存、操作、计算和表示有一定的困难;网格地图对实际地图进行了一定程度的抽象，坐标值是整型，蚂蚁的行动限制在上、下、左、右四个方向上，使得路径的保存、操作和计算方便简单，网格表示路径直观易懂，但是对于障碍物，特别是障碍物范围的表示不够明确清晰，这对判断蚂蚁是否遇到障碍物造成了较大的困难;位图地图类似于网格地图，坐标值也是整型，蚂蚁的行动也有四个方向上的限制，但是位图能明确表示障碍物及其范围，而且位图的每个像素相互独立.基于以上三种地图的特点，本研究选择位图地图来表示区域地图上的地理信息和路径.

虽然位图地图只是实际地图的抽象，但在实际应用中，只要像素细化到一定程度，就可以无限近似于实际地图.对位图地图上像素点的属性进行设置:

1)坐标.用于定位.

2)类型.0表示可行地区，1表示高山或者山脉，2表示山谷，3表示河流，4表示城镇.

3)权值.类型为0、1、2、3的像素点权值设为0.类型为4的城镇像素点权值取值为1～10之间的一个整数值，权值越高表示城镇越发达越重要.在遇到城镇时由权值的大小来判断是绕开城镇、架设高架桥通过城镇还是进行征地直接修建高速公路.

4)信息素值.保存每个像素点上的信息素值.该值会随着经过的蚂蚁和时间的变化而变化.终点的像素值被赋予一个极大值，不会改变.

5)经过标志.为每只蚂蚁设置像素点经过标志.0表示某只蚂蚁未走过该像素点，1表示蚂蚁已走过该像素点.为实现蚂蚁行走路线不形成回路，任意蚂蚁下一步只能选择标志为0的像素点.

对于以上地图像素点的属性，除了信息素浓度和经过标志在系统运行时会发生改变之外，其他属性初始化之后一般不会再改变.

1.2 建立数学模型

修建高速公路的造价可转换为修建高速公路所需的时间.假定普通情况下修建每公里需要时间为t1，架设高架桥、开凿隧道、征用居民用地等的造价分别转换为普通情况下造价的X、Y、Z倍，相应的修建时间可转化为普通情况修建时间的X、Y、Z倍.假设建设一条高速公路的总长度为L，其中普通路段长度为L1、高架桥路段长度为L2、开凿隧道路段长度为L3、征用居民用地路段长度为L4，则修建这条高速公路需要的时间为:

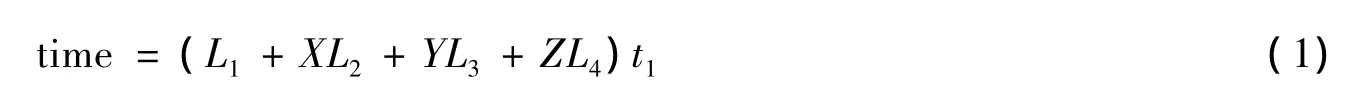
因此，修建造价最小的高速公路转化为式(1)取得最小值.

在位图地图上，蚂蚁从当前位置出发可以有上、下、左、右4个行进方向，到达相邻像素点需要一步.假设从起点到终点的规划路径上依次经过位图上的m个像素点，xi，i+1为从i点到i+1点的行进距离，位图方式下设为一个距离单位，i=1，2，…，m－1.从i像素点到i+1像素点的行进时间为ci，i+1，普通路段行进时间需要一个时间单位，修建高架桥、开凿隧道、征用居民用地路段的行进时间设为普通路段的相应倍数.设蚂蚁从起点到终点的行进时间为w，则数学模型为:

约束条件:

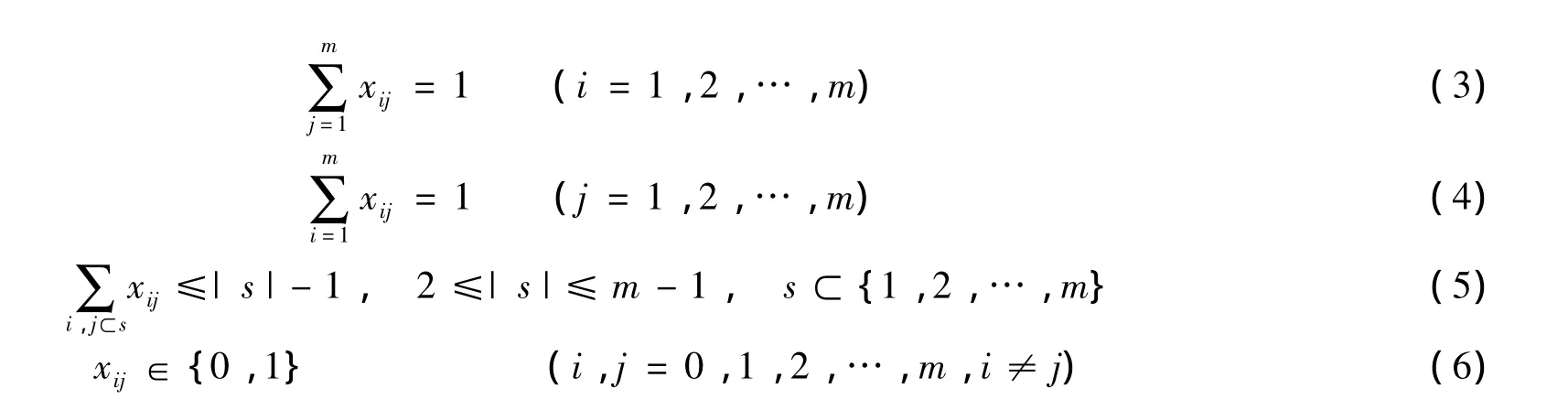
xij=0表示蚂蚁没有走i和j之间的路径，xij=1表示蚂蚁走了i和j之间的路径.在位图方式下，蚂蚁只能走相邻的像素点.式(3)表示只从i点走出来一次;式(4)表示只走入j点1次;式(5)表示在任意点之间不形成回路.

1.3 遇到障碍物的处理

蚂蚁从像素点i行走到达像素点i+1，如果像素点i+1的类型值为1或者2或者3，表示蚂蚁遇到了高山或者山谷或者河流，则该蚂蚁有一定的较小概率ζ因为遇到障碍物走入死角死亡，借鉴蚁群算法引入侦查子群［8］和生物可变异的思想，让蚂蚁以1－ζ的概率变异成一种特殊蚂蚁，可通过相应的方法(架设高架桥或者开凿隧道)穿过障碍物.

如果像素点i+1的类型值为4，表示蚂蚁遇到了城镇.此时判断像素点i+1的权值，如果权值大于等于5，表示遇到的是主要城市，不适合架设高架桥，蚂蚁就因为遇到障碍物走入死角死亡;如果权值小于2，表示是偏远小村落，可以进行征地直接修建高速公路;如果权值小于5并且大于等于2，表示可以对这个城市架设高架桥，则蚂蚁有一定的较小概率ζ因为遇到障碍物走入死角死亡，以1－ζ的概率变异成特殊蚂蚁，能通过架设高架桥穿过该城镇.对于这些能够通过障碍物的特殊蚂蚁，蚂蚁的行进时间为:

2 算法

2.1 设置每只蚂蚁属性

1)蚂蚁的坐标.用于表示每只蚂蚁的当前位置.初始化为起点坐标.

2)蚂蚁的生存时间.用于保存每只蚂蚁从起点出发行进到当前位置花费的时间，当超过最大值T时表示蚂蚁死亡.初始化为0.到达终点且生存时间最小即为最优解.

3)蚂蚁的障碍物标志.用来记录蚂蚁遇到的障碍物的长度.与障碍物类型有关，并且遇到的障碍物越长，延时越长.初始化为0.

4)蚂蚁到达终点标志.用来标记每只蚂蚁是否到达终点.初始化为0，到达终点为1.

5)路径.用于保存每只蚂蚁走过的路径.

2.2 更新信息素

在基本蚁群算法中，每只蚂蚁都可以到达终点并在它经过的路径上留下信息素.在本文中，蚂蚁在寻径过程中会由于超时或遇到障碍物而死亡，因此，可把能够到达终点并且没有超时的蚂蚁看做精英蚂蚁，只有精英蚂蚁k到达终点后才按照式(7)更新其经过路径上的信息素:

其中:timek表示精英蚂蚁k搜寻路径的时间;ρ为局部信息素挥发系数，ρ值越大表示信息素的影响越小.

为进一步增强最优蚂蚁的作用，迭代一次后，按照式(9)更新目前搜索到的最优路径上的信息素，加强蚁群算法的正反馈作用［9］.

其中:besttime表示当前最短搜寻路径时间;γ是全局信息素挥发系数，γ值越大表示信息素的影响越小.

如果一次迭代中有多只蚂蚁搜寻到了最优路径，那么这几条最优路径都按式(9)进行信息素更新.

2.3 设置延时系数

在改进的蚁群算法中，需将架设高架桥、开凿隧道和征用土地等转换为修建普通路段时间的相应倍数，设置相应的延时系数.这三个系数与蚂蚁穿过障碍物的长度直接影响蚂蚁对最优路径的选取，因此它们的取值非常重要.

一般障碍物分为狭长形和宽广型.实际障碍物在位图中抽象成规则形状，如图1中的阴影部分所示，但障碍物的范围和走向不同.图1中的“⊕”字符表示起点和终点，实线箭头表示蚂蚁绕障碍物行走路线，虚线箭头表示蚂蚁穿过障碍物行走路线(参照实际穿过障碍物时一般采用直线路线).

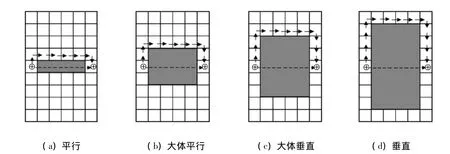
图1 障碍物和起点、终点走向关系图Fig.1 Diagrams of obstacles and start，and point

表1 穿过和绕开障碍物步数对比表Tab.1 Comparison of passing or bypassing obstacles

图1四种情况下蚂蚁穿过障碍物和绕开障碍物步数对比如表1所示.从表1可以看出，随着障碍物和起点、终点走向由平行变为垂直，蚂蚁穿过障碍物需要行走步数不变，但是绕开障碍物需要行走的步数在不断增加.在二者走向是平行时，绕开与穿过步数比值小于2;而二者走向是垂直时，绕开与穿过步数比值大于2，小于3.如果图1(d)中障碍物沿走向再继续延长，蚂蚁绕开障碍物需要行走更多步，绕开与穿过障碍物的步数比值将会更大.因此延时系数的范围可选择在2～3之间.

结合在实际工程中，开凿隧道工程难度最高、花费也最大，架设高架桥最常用且工程难度中等，征用土地工程难度较小，因此开凿隧道延时系数relaytime1最大，架设高架桥延时系数relaytime2次之，征用土地延时系数relaytime3最小.程序选择relaytime1=2.8、relaytime2=2.6、relaytime3=2.2这一组数据做了测试，测试结果说明，这样的系数设置较合适.

2.4 定义每只蚂蚁的行动规则

蚂蚁在前进时会受到信息素的吸引，根据信息素浓度决定转移方向.在位图方式下，每只蚂蚁只有上、下、左、右4个方向可走.蚂蚁k在t时刻从i像素点出发选择j像素点的转移概率如式(11)所示.

其中:allowedk表示蚂蚁k可选择方向的集合;α是信息素启发因子，表示信息素浓度在蚂蚁选择路径中作用的大小.

为增加探索新路径的机会，蚂蚁有一定的概率随机选择前进方向.定义蚂蚁的行动规则如下:

①判断蚂蚁是否能走下一步.对于生存时间小于最大值T且没有到达终点的蚂蚁，进行步骤②;否则这只蚂蚁已经死亡.

②蚂蚁选择下一步的坐标.如果一只蚂蚁当前处在起点处，则比较起点坐标和终点坐标，让蚂蚁有较大概率走某个方向;否则排除蚂蚁上、下、左、右已经走过的方向，蚂蚁有一定的概率不被信息素的浓度吸引，而是随机选择向可走的方向走一步，蚂蚁进入步骤④;或者蚂蚁被信息素浓度吸引，蚂蚁进入步骤③.

③按式(11)计算可走方向的转移概率，选择转移概率最大的方向.

④判断步骤②或步骤③计算的蚂蚁的下一步坐标:

如果坐标为终点坐标，表示这一只蚂蚁完成了寻径过程，更新该蚂蚁当前坐标，记录蚂蚁行进方向，计算生存时间，到达终点的标志记为1.

如果坐标对应的像素点类型为0，表示下一步蚂蚁没有遇到障碍物，则更新蚂蚁的当前坐标，记录蚂蚁行进方向，该像素点的经过标志置1，计算其生存时间;否则蚂蚁遇到了障碍物，按遇到障碍物处理，如果蚂蚁可通过障碍物变为特殊蚂蚁，障碍物长度+1，更新其坐标，记录蚂蚁行进方向，该像素点的经过标志置1，为其计算生存时间.

⑤重复上述步骤①直至蚂蚁死亡或到达终点.

2.5 保存蚂蚁行进路径

考虑到蚂蚁的行进方向只有上、下、左、右4种可能，上、下、左、右4个方向分别用1、2、3、4数值表示，所以在保存蚂蚁的路径时，只保存1～4之间的某一个整数值来表示蚂蚁每一步行进的方向，而未保存每一步的坐标.只有当一只蚂蚁到达终点后的生存时间最短时再将其路径转换成坐标值.这样路径保存的数据量减少了一半.

2.6 算法伪代码

1)read要修建高速公路的起点坐标、终点坐标;

2)初始化地图信息;

3)位图上所有像素点的经过标识初始化为0;

4)初始化迭代次数N，每代蚂蚁数量m;

5)set最小寻经时间besttime=T;

9)计算最小搜寻时间besttime对应的最优路径，保存路径;

10)输出最优路径.

3 实验

3.1 初始化区域地图

初始化一个如图2所示的位图地图，图中的“－”字符表示平地，“1”字符部分表示山谷，“～”字符部分表示河流，“#”字符部分表示高山或者山脉，“4”字符部分表示城镇.地图横坐标为［0，99］，纵坐标为［0，99］，坐标原点在左上角.

3.2 搜寻最优路径

在实验中，蚂蚁的迭代次数和种群数均设定为100.以地图中的起点坐标［43，17］和终点坐标［72，85］为例，测试变异蚁群算法的α、ρ、γ 3个参数.实验中为每一个参数设定一组值，ρ∈{0.1，0.2，0.3，0.5，0.7，0.9}，γ∈{0.1，0.2，0.3，0.5，0.7，0.9}，α∈{0 ，0.5，1，2，5}.每次实验只改变其中一个参数的值，其他参数保持不变.为降低偶然因素的影响，每组参数仿真10次，取10次实验的平均值、最优值、最差值作比较，以此来分析参数取值对算法性能的影响.设α=1，ρ=0.3，γ=0.4为默认参数值.实验结果如表2所示.

在表2中，当设定α=1，γ=0.4时，ρ∈［0.2，0.3］得到的解是较优的;当α=1，ρ=0.3时，γ=0.2得到的解是较优的;当设定ρ=0.3，γ=0.4时，α∈［0.5，1，2］得到的解是较优的.所以可以得出，设定α=1、ρ=0.2、γ=0.2较为合适.

同样以图2所示的地图中的起点坐标［43，17］和终点坐标［72，85］为例，设定参数α=1、ρ=0.2、γ=0.2对变异蚁群算法仿真10次，得到最优时间 besttime为104.0，最长时间为127.6，平均时间为113.8.通过对比仿真结果与表2中的数据说明，参数的取值是有效的.当参数α=1、ρ=0.2、γ=0.2时对可变异和不变异蚁群算法分别进行测试，测试搜索到的最优路径分别如图3的(a)和(b)中起点至终点的连线所示.在图3(a)中蚂蚁遇到障碍物可变异成一种特殊蚂蚁穿越山脉和河流，最优时间besttime为104.0.而在图3(b)中，蚂蚁没有变异，不可穿越障碍物，只能绕着障碍物行走，最优时间besttime为120.0.仿真10次得到的最优时间besttime为120.0，最长时间为149.0，平均时间为136.8.通过数据对比说明，挖隧道经过山脉、架设高架桥通过河流、绕过中等权值城市的路径是造价最小的.

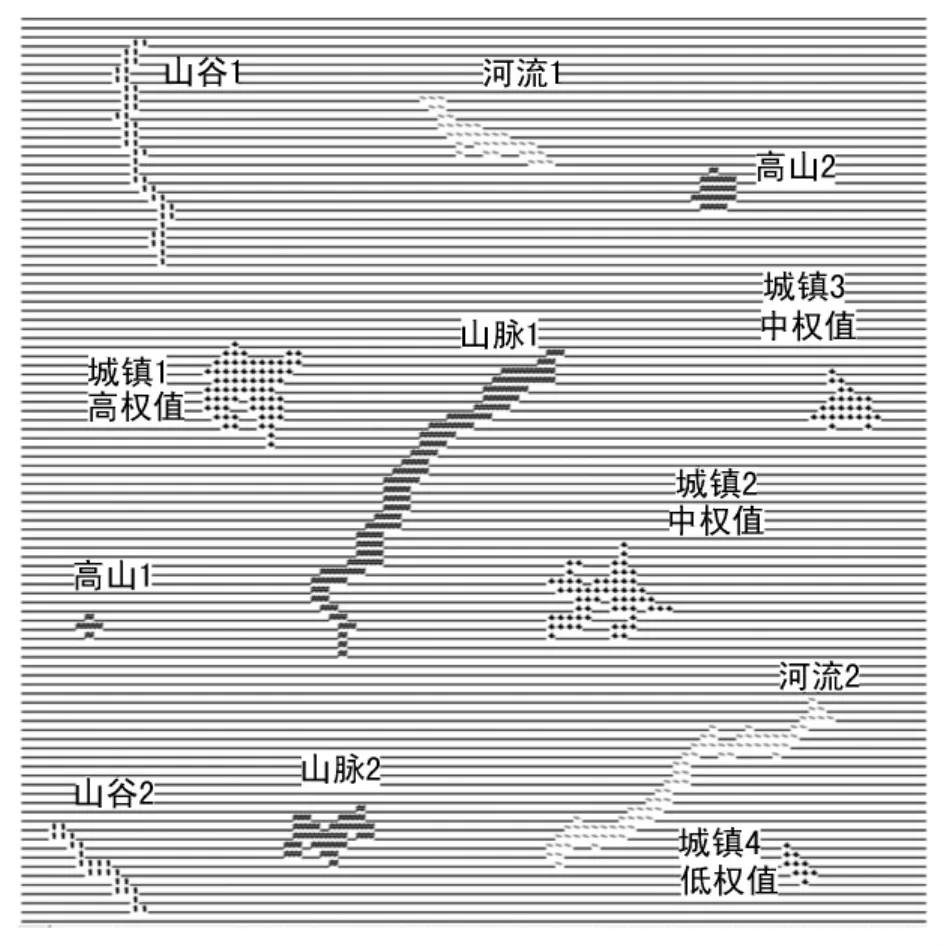
图2 拟修建高速公路的区域地图Fig.2 Regional map of the highway to be constructed

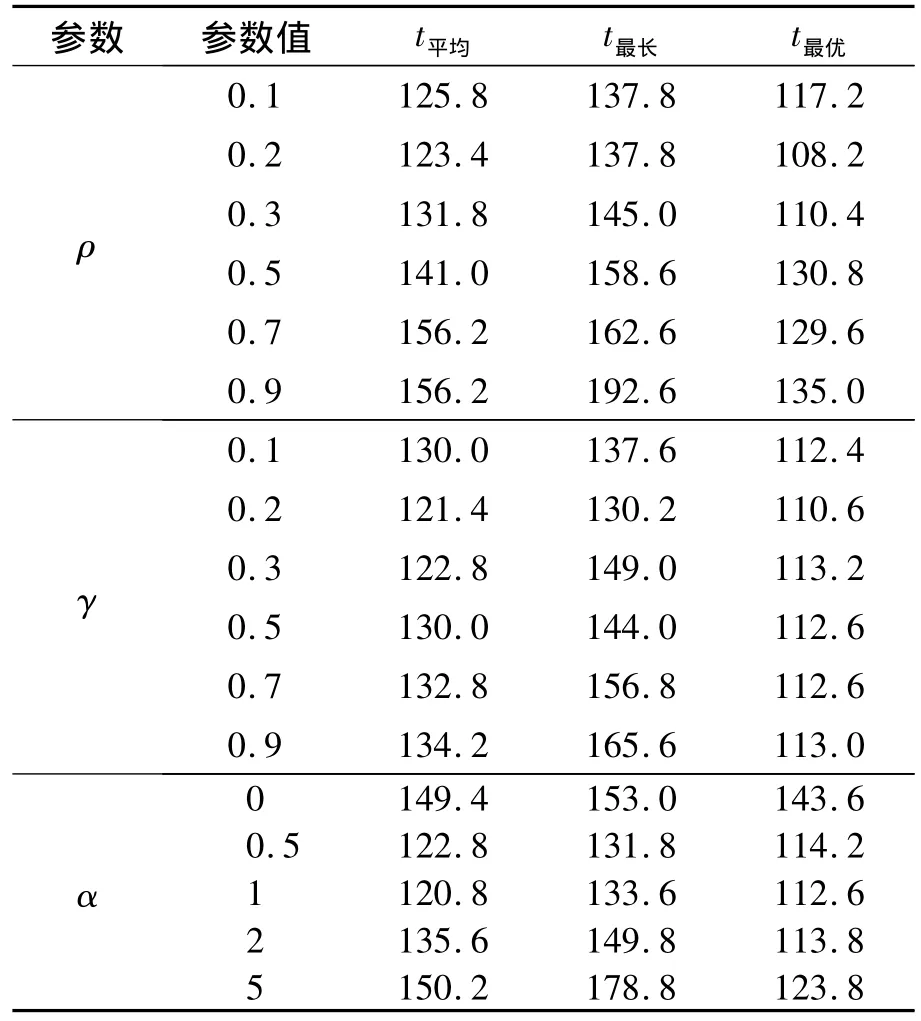
表2 变异蚁群算法各参数测试结果Tab.2 Test results of the parameters of the mutated ant colony algorithm

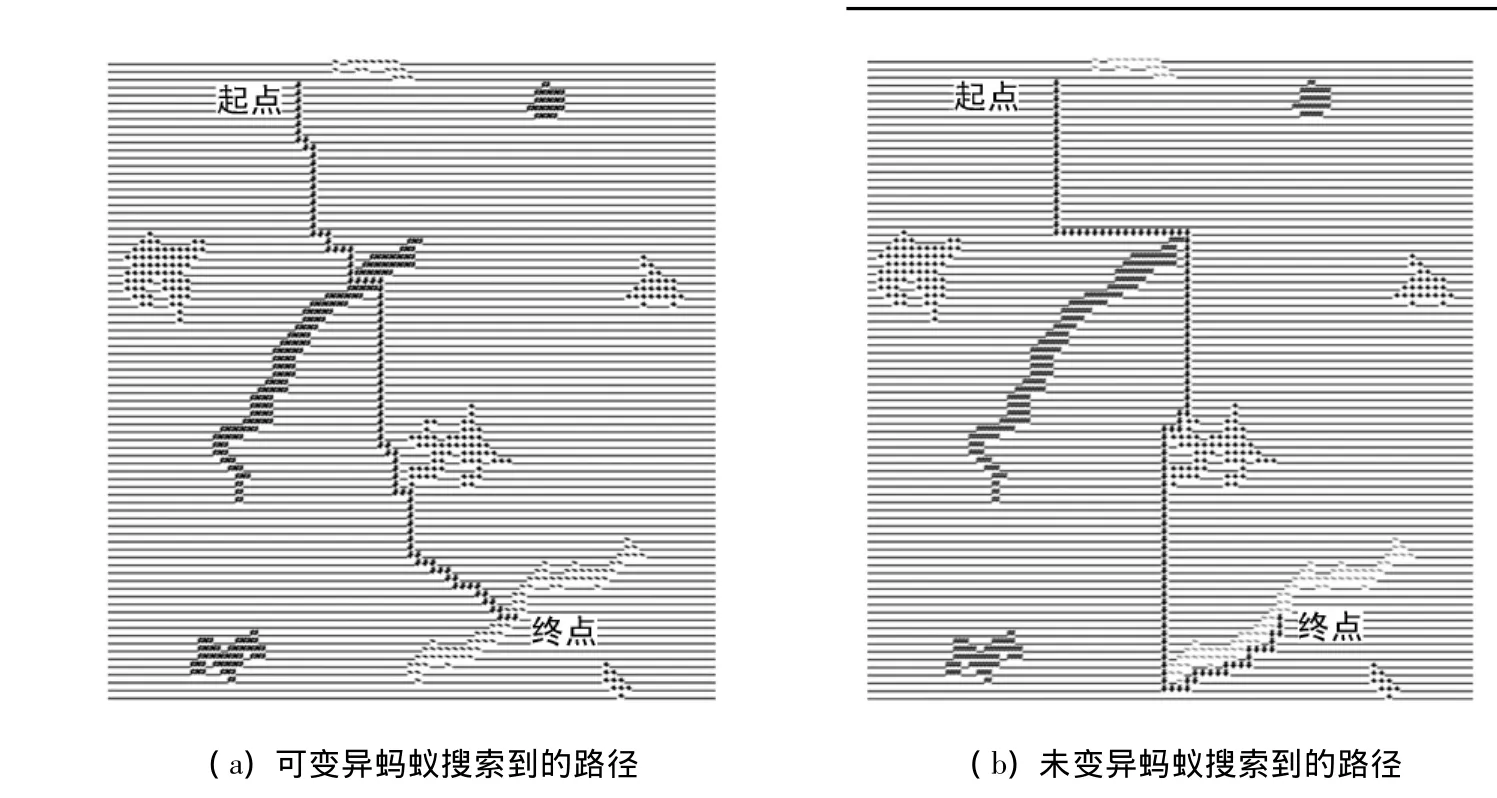
图3 最优路径Fig.3 Optimal path

4 结语

蚁群算法是一种启发式的随机搜索技术，具有鲁棒性、正反馈等特点.考虑到高速公路路线规划问题的特殊性，利用生物进化过程中可能出现的变异特性，对蚁群算法做了一些改进，使得蚂蚁种群中的部分蚂蚁可以变异成一种特殊蚂蚁，通过架设高架桥、穿凿隧道等方式穿越障碍物，可搜寻出一条造价最小的修建路线.

由于采用位图地图来表示地理信息，蚂蚁的行进路线只有上、下、左、右4个方向，所以不可避免的在搜寻高速公路路径时出现了垂直角度的路线，这不符合高速公路不能出现直角路线的要求，所以本文的高速公路选径研究离真正的选径路线还有一定的差距，但在实际应用时有一定的指导意义.本文的研究是规划高速公路路线的一种新理论方法的探索，也为其他道路设施如高速铁路的规划建设，提供了一些参考依据.智能算法应用于高速公路建设对未来合理、智能地规划道路具有一定的参考意义.

［1］Porta Garcia M A，Oscar M，Oscar C，et al.Path planning for autonomous mobile robot navigation with ant colony optimization and fuzzy cost function evaluation［J］.Applied Soft Computing，2009，9(3):1 102 －1 110.

［2］Mei Hao，Tian Yan－tao，Zu Li－nan.A hybrid ant colony optimization algorithm for path planning of robot in dynamic environment［J］.International Journal of Information Technology，2006，12(3):78 －88.

［3］Zhu Qing－bao，Hu Jun，Cai Wen －bin，et al.A new robot navigation algorithm for dynamic unknown environments based on dynamic path re－computation and an improved scout ant algorithm［J］.Applied Soft Computing，2011，11(8):4667－4 676.

［4］温如春，许樱，王祖麟.改进蚁群算法在迷宫路径规划问题中的研究和应用［J］.江西理工大学学报，2010，31(2):26－28.

［5］张维泽，林剑波，吴洪森，等.基于改进蚁群算法的物流配送路径优化［J］.浙江大学学报:工学版，2008，42(4):574－578;597.

［6］吴建军，刘军.物流配送路径安排问题的混合蚁群算法［J］.土木工程学报，2004，37(8):98－101.

［7］Duran T M.Ant colony optimization for finding the global minimum［J］.Applied Mathematics and Computation，2006，176(1):308－316.

［8］胡中华，赵敏，姚敏.引入侦查子群的二进制蚁群算法求解函数优化问题［J］.小型微型计算机系统，2010，31(6):1 175－1 179.

［9］朱庆保，杨志军.基于变异和动态信息素更新的蚁群优化算法［J］.软件学报，2004，15(2):185－192.