函数问题寻解 以形助数逞能——以2013年江苏卷第20题为例谈以形助数“三好”

☉江苏省锡山高级中学 吴宝莹（特级教师）

☉江苏省锡山高级中学 王良骏

数形结合是“数”与“形”相互转化的研究策略，即把数量关系的研究转化为图形性质的研究，或者把图形性质的研究转化为数量关系的研究，数形结合是重要的数学思想，又是常用的数学方法.显然，数形结合的应用大致可分为两种情形：第一种情形是借助形的几何直观性来阐明数之间的某种关系，即“以形助数”；第二种情形是借助于数的精确性来阐明形的某些属性，即“以数解形”.第二种情形“以数解形”已经形成一门成熟的学科——解析几何，这里重点谈谈第一种情形“以形助数”的“三好”.

一、作图好

在中学数学中，“形”的广义性以及学生数学学习中直觉形象思维的主导地位决定了大部分数学知识学习需要“形”的支撑.如数学概念的建立借助“形”的直观、数学性质的探索通过“形”的操作、数学规则的形成以“形”做材料、解题思路的获得用“形”来帮助等.以形助数，作图解决问题好处多多，亦即“作图好”，下面以2013年江苏高考数学卷第20题为例说明.

题目：设函数f（x）=lnx-ax，g（x）=ex-ax，其中a为实数.

（1）若f（x）在（1，+∞）上是单调减函数，且g（x）在（1，+∞）上有最小值，求a的取值范围；

（2）若g（x）在（-1，+∞）上是单调增函数，试求f（x）的零点个数，并证明你的结论.

解：（1）略.

当0＜x＜e时，h′（x）＞0，h′（x）单调递增且连续不断；当x＞e时，h′（x）＜0，h′（x）单调递减且连续不断.

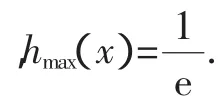
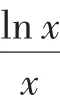
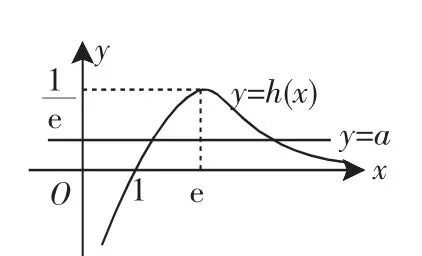
图1

f（x）的零点个数转化为图像交点个数问题，通过作图解决，形象直观，简便可行.而函数的单调性是函数的重要性质，决定了函数图像的变化走势，导数又是研究函数单调性的有力工具，所以本题从导数入手，借助图形，解决f（x）的零点个数问题.

二、作好图

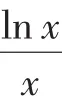
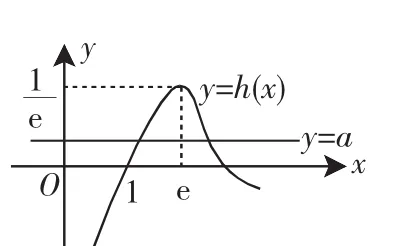
图2

三、好作图

以形助数是借助形的几何直观性来研究代数问题，但是同一个代数问题有时不止用一种形来助数，好作图即容易作图，就是通过转化，选择容易作的图形来助数，以达到研究代数问题的目的.

本例题第（2）问江苏命题组给出的标准答案如下：

解：（2）当a≤0时，g（x）必为单调增函数；当a＞0时，令g′（x）=ex-ax＞0，解得a≤ex.即x＞lna，因为g（x）在（-1，+∞）上是单调函数，类似（1）有lna≤-1，即0＜a≤e-1.结合上述两种情况，有a≤e-1.

（ii）当a＜0时，由于f（ea）=a-aea=a（1-ea）＜0，f（1）=-a＞0，且函数f（x）在［ea，1］上的图像不间断，所以f（x）在（ea，1）上存在零点.

当0＜x＜a-1时，f′（x）＞0，

当x＞a-1时，f′（x）＜0，所以，x=a-1是f（x）的最大值点，且最大值为f（a-1）=-lna-1.

①当-lna-1=0，即a=e-1时，f（x）有一个零点x=e.

②当-lna-1＞0，即0＜a＜e-1时，f（x）有两个零点.

实际上，对于0＜a＜e-1，由于f（e-1）=-1-ae-1＜0，f（a-1）＞0，且函数f（x）在［e-1，a-1］上的图像不间断，所以f（x）在（e-1，a-1）上存在零点.

下面考虑f（x）在（a-1，+∞）上的情况，先证f（ea-1）=a（a-2-ea-1）＜0.

为此，要证明：当x＞e时，ex＞x2.

设h（x）=ex-x2，则h′（x）=ex-2x.

再设l（x）=h′（x）=ex-2x，则l′（x）=ex-2.

当x＞1时，l′（x）=ex-2＞e-2＞0，所以l（x）=h′（x）在（1，+∞）上是单调增函数.故当x＞2时，h′（x）=ex-2x＞h′（2）=e2-4＞0，从而h（x）在（2，+∞）上是单调增函数，进而当x＞e时，h（x）=ex-x2＞h（e）=ee-e2＞0.即当x＞e时，ex＞x2.

当0＜a＜e-1，即a-1＞e时，f（ea-1）=a-1-aea-1=a（a-2-ea-1）＜0.又f（a-1）＞0，且函数f（x）在［a-1，ea-1］上的图像不间断，所以f（x）在（a-1，ea-1）上存在零点.

综合（i），（ii），（iii），当a≤0或a=e-1时，f（x）的零点个数为1，当0＜a＜e-1时，f（x）的零点个数为2.

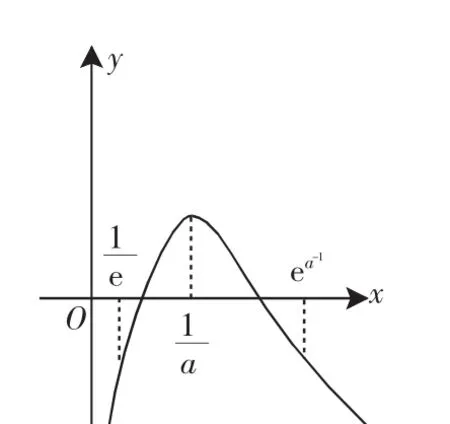
图3

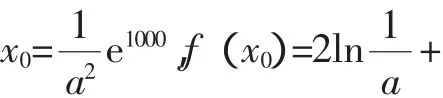
总而言之，通过适当转化，遵循好作图的原则，准确作图，作好图，才能凸显作图好的优势.但是，“形”虽具有形象直观的优势，但也有其粗略、烦琐和不便于表达的劣势.只有以简洁的数学描述、形式化的数学模型表达“形”的特性，才能更好地体现数学抽象化与形式化的魅力，从而更准确地把握“形”.正如我国著名数学家华罗庚教授所说：“数缺形时少直觉，形少数时难入微，数形结合百般好，隔离分家万事非.”数与形是辩证统一关系，“以形助数”与“以数解形”是数形结合的左膀右臂，不可偏驳.