赛场命题天然成 真题真解真思想——2013年全国高中数学联赛湖北省预赛填空题详解

☉湖北省浠水县实验高级中学 程贤清 占巧月

2013年全国高中数学联合竞赛湖北省预赛试卷分高一年级卷和高二年级卷，每份试卷均设计10道填空题和3道解答题.命题组提供的参考答案对填空题只给出结果，未做详解.为了帮助同学们在学习、研究中有所启发和参照，本文对高二试卷中所有填空题做出详解分析和点评.

分析：由集合C中代表元素为a+b，且a∈A，b∈B，可用列举法写出集合C={3，5，7，9，11，13，15，19，21，23，25，27}，从而集合C的所有元素之和为（3+5+7+…+27）-17=195-17=178.

点评：本题考查了考生对集合概念的本质理解及计算的灵活性.易错点有：①未去掉生成集合C时的重复元素；②不会转化为等差数列求和.

2.已知数列{an}满足：a0=0，a1=1，且a2n=an，a2n+1=an+1（n∈N*），则a2013=_________.

分析：由递推关系可知，无论下标为奇数还是偶数，都可以迅速将下标缩小.据此，反复使用递推关系，即可求得结果.a2013=a1006+1=a503+1=a251+2=a125+3=a62+4=a31+4=a15+5=a7+6=a3+7=a1+8=9.

点评：本题重点考查了转化思想和解题方法的选择判断能力.本题易错点有：①欲求出通项，思路受阻；②平时训练过此类题，大多是周期数列，因而部分考生很想求出该数列的周期，但由于此题无法求出周期（本不是周期数列）而出现思路中断；③不了解a0这个条件怎么用，产生畏惧心理.实际上这里a0是数列的首项，a1是数列的第二项.设置a0的目的是考查考生解题的抗干扰能力.事实上本题去掉a0=0这个条件，不影响解题结果.

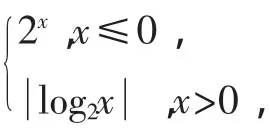
分析：由已知得F（1，0）.设P（x，y），M（x0，y0），则过点M的切线方程为集为_________.

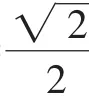
点评：本题主要考查分段函数的概念，指数、对数、绝对值的运算及分类讨论思想.本题易错点是对数及其绝对值的运算.

点评：本题考查的知识有同角三角函数关系，二倍角公式，正弦函数有界性，二元均值不等式.考查的方法是利用均值不等式及正弦函数的有界性进行连续放缩.该法能够成功的关键在于多次放缩时，等号能同时成立.本题易错点是不能合理分组进行连续放缩.

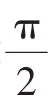
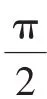
有P=2cos2x-2cos2y-4cosx+4cosy

=2（cosx-1）2-2cos2y+4cosy-2

≥-2cos2y+4cosy-2=2cosy（2-cosy）-2＞-2.

又有P=2（cosx+cosy-2）（cosx-cosy）＜0.

综上所述，有P∈（-2，0）.

点评：本题主要考查余弦函数的单调性、二次函数的性质以及三角恒等变换、放缩变换的能力.解题难点是所求范围的两个界点需要用两种不同的思路进行求解.本题易错点是不能准确求出两个界点值，导致所求范围扩大.

图1

①-②×4得（x0-4）（x-4）=0.又-2≤x0≤2，

故x-4=0，即x=4为所求点P的轨迹方程.

点评：本题考查了椭圆的切线方程、向量的数量积等知识以及代数的消元变形能力.易错点是列出相关条件方程后不知如何变形运算.

7.从集合A={1，2，3，…，30}中取出5个不同的数，使这5个数构成等差数列，则可以得到不同的等差数列的个数为_____________.

分析：按公差分别为1，2，3，…，7进行分类（先考虑公差为正数的个数）：

公差为1的等差数列有1，2，3，4，5；2，3，4，5，6；…；26，27，28，29，30.共26个.

公差为2的等差数列有1，3，5，7，9；2，4，6，8，10；…；22，24，26，28，30.共22个.

……

公差为7的等差数列有1，8，15，22，29；2，9，16，23，30.共2个.

故构成公差为正数的不同等差数列的总个数为26+22+18+…+6+2=98.

又公差为负数的不同等差数列的个数也为98.

故所求不同的等差数列的个数为98×2=196.

点评：本题主要考查集合及等差数列的概念，数列求和等知识和分类讨论的策略和意识.本题易错点是易漏掉计算公差为负数的情形.

8.四面体P-ABC的体积为1，G和K分别是△ABC和△PBC的重心，过G作直线分别交AB，AC于点M，N，那么四棱锥K-MNCB的体积的最大值为__________.

分析：如图2，连接PK并延长交BC于Q，过P作PO⊥面ABC，垂足为O，连接OQ.由PO⊥面ABC知面POQ⊥面ABC，过K作KR⊥OQ于R，则KR⊥面MNCB，KR为四棱锥K-MNCB的高.记四面体P-ABC的底面积为S，高PO=h.

图2

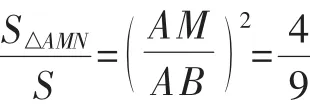
点评：本题是一道立体几何综合题.重点考查了空间问题平面化策略以及运动变化思想的应用.涉及的几何知识有：重心概念及重心定理，相似三角形的有关性质，棱锥的体积公式.本题易错点有：①不能准确画出空间图形或画出的图形粗糙，线条重叠，妨碍思考；②不善于运用平面化的策略及运动变化思想对问题进行逐步简化.

9.已知互不相等的三个实数a，b，c成等比数列，且logca，logb c，logab构 成 公 差 为d的 等 差 数 列 ， 则d=__________.

分析：因为a，b，c成等比数列，所以b2=ac，两边同取以b为底的对数得：

①代入②整理得2x3-9x2+9x-2=0.

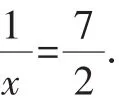
点评：本题是高一试卷中的解答题12题，此处最后两步运用整体思想处理较命题组参考答案的解法更为简捷，有效地避免了直接解方程再分类讨论的烦琐运算.

本题考查了等差数列、等比数列的概念，对数的运算性质，换底公式等知识，还考查了换元（简化）转化，整体代入等重要数学思想方法.结合式的运算对考生思维能力和运算技巧的结合进行了深刻考查.试题设计精巧，下手易，深入难.解决本题的关键有：①是对b2=ac两边取对数；②是对已知对数式换元.本题易错点是根据已知条件直译列出方程后不知如何运算，换元转化意识不强.

10.已知a，b，c，d∈［-1，+∞），且a+b+c+d=0，则ab+bc+cd的最大值为_______.

分析：本题为多变元求最值问题，可尝试逐步消元（减元）.比如，消去d得，ab+bc+cd=ab+bc-c（a+b+c）=abac-c2=a（b-c）-c2.为便于放缩，继续消元，可对b，c的大小关系进行分类讨论.

（1）若b≤c，则由a≥-1，b-c≤0知a（b-c）≤-（b-c）有

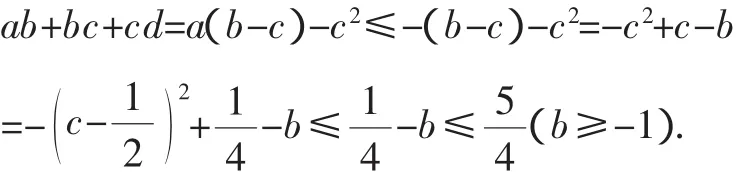
由d≥-1，c-b≤0知d（c-b）≤-（c-b），

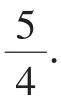
点评：本题是一道区分度较大的难题，竞赛味浓.着重考查考生的代数推理能力 （尤其是不等式的放缩变形能力）.本题易错点是放缩变形方向不明.本题的放缩技巧很值得我们思考与回味.