有效利用数学错题集，培养学生的思维品质

☉江苏省栟茶高级中学 张 飞

错题集是学生在学习过程中，把自己做过的作业、习题、试卷中的错题整理成册，便于找出自己学习中的薄弱环节，在复习时能够突出重点、更有针对性，进而提高复习效率、提高学习成绩.本学期笔者尝试指导学生使用错题集来搜集典型错题，通过错题集进行数学反思、培养学生良好的学习态度和习惯，指导学生学会归纳分析、梳理，抓住问题的关键，条理化、系统化地解决问题；通过错题集解决零散、疏漏等问题，通过一学期的实践，有效使用错题集，可以培养优良数学思维品质，具体表现为思维的严密性、广阔性、深刻性、独创性及批判性等数学思维品质.

一、经常阅读，查漏补缺，培养数学思维的严密性

错题集不是简单的错题的集中，它需要学生经常把其中的错题拿出来复习，重新再做，体会其中的方法，这样就使每一道题都发挥出最大效果，在今后遇到同类习题时，就避免在同一个地方摔倒.这样经常温故知错、持之以恒，学生的成绩就会得到提高.

案例1 （1）△ABC中，A（0，-1），B（0，1），A，B，C所对的边分别为a，b，c，且a，c，b构成公差大于0的等差数列，则顶点C的轨迹方程为______.

学生都能解出方程，但忽视了限制条件：能构成三角形而且公差大于0.

（2）对概念学习的反思.

生1：今天学习了椭圆的定义，我用代数式表示：

E（-2，0），F（2，0），EF=4，令P（x，y），则

（3）对出错题的反思.

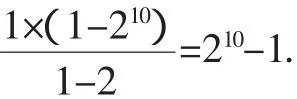
又1+2+22+…+210有11项，

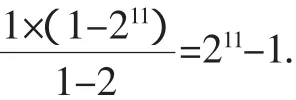
让学生整理错题集，一方面可以完善学生对知识的理解，拓宽学生的思维方式，提高解题能力，另一方面，老师通过阅读学生的错题集，了解学生的学习情况，及时调整教学计划，同时促进师生之间的交流.

二、相互交流，必要补充，培养数学思维的广阔性

由于基础不同，每个学生的错题集各不相同.通过交流，学生之间可以相互借鉴，提醒自己不要犯同样的错误，提高做题的效率.

生3的错误解法：设F1（-c，0），F2（c，0），在△F1PF2中用余弦定理，得到：

化简得：

对①式两边平方，化简得c2=4或16.再由点在椭圆上，解出a2，b2的值.

事实上，①式隐含了条件16-2c2≥0，所以c2=16舍去.在整理错题时可以注明，化简的过程要等价，另外，还可以补充其他同学的做法.

生4：设PF1=m，PF2=n，由椭圆的定义及在△F1PF2中用余弦定理得：

由①，②可解出a2=10，b2=6.

当然，生3的错误对其他同学也是个警示，其他同学也可以把他的错误标注在自己的错题集上.

对于每一个错题，你应该能从各个方面理解它，补充多种解法，否则，在下一次测试中，对于这一问题的处理再深入一点，你可能还要犯同样的错误.

三、注重联系，联想转化，培养数学思维的深刻性

在教学活动中，学生对很多数学问题无从下手.学生订正错题后，此时的关键是教师如何让学生的思维逐步上升到能揭示知识间内在的本质属性.所以在做错题集的过程中，培养学生善于洞察数学对象的本质属性及相互关系；善于消去条件与结论的本质差异，寻找解决问题的突破口，迅速确定解题策略并形成解题方法，即培养学生数学思维的深刻性.

CRD法虽然已经被广泛地应用于大断面浅埋偏压隧道的建设，但仍存在一定的技术问题，主要包括施工指导问题和防排水技术问题，这或多或少地导致大断面浅埋偏压隧道建设存在一些问题。

学生在订正题后，可以引导学生联想到，若把双曲线改为椭圆，则以PF1为直径的圆和哪个定圆相切？

通过引导，看似不同的题目，其解决的方法和思想都是一样的，都可以用圆锥曲线的定义来解决.由此可见，学生订正完一道题后，会经常注意反思此题的思想方法是否可以做一般性的推广与引申，长此以往，学生可以巩固他们的知识和发展他们的解题能力，形成数学思想，提高解题能力，同时培养了数学思维的深刻性.

四、错题改编，善于思考，培养数学思维的独创性

这一工作的难度较大，解题经验丰富的同学可能做起来比较顺利.很多同学在解了很多题目之后，对有些题型能够准确把握.初始阶段，学生只需要对题目做一点改动.如：考虑条件与结论交换是否成立？考虑一般的情况会怎样？

案例4 已知直线y=x-2与抛物线y2=2x相交于点A，B，则∠AOB=_____.

学生在订正完后，可以引导学生将此题改编：

将直线一般化：

（1）直线l过（2，0），交抛物线y2=2x于A，B两点，则∠AOB=______.

将条件与结论交换，证明充要性：

（2）已知直线l交y2=2x于A，B两点，且OA⊥OB，证明：直线l过（2，0）.

将结论一般化：

（3）已知直线l交y2=2px（p>0）于A，B两点，且OA⊥OB，证明：直线l过（2p，0）.

将点O位置一般化：

（4）已知直线l交y2=2px（p>0）于A，B两点，M是抛物线上一点，且MA⊥MB，证明：直线l过定点.

在学生做错题集的过程中，只要学生的思考方式方法新颖，独特，教师应该不吝表扬，鼓励学生善于动脑，培养学生思维的独创性.

五、典型错误，善于积累，培养数学思维的批判性

开始错题集里浅显的错误会占大多数，随着错题的积累，错题集中的错误层次会越来越高.

学生通过积累典型错误，发现在前3种解法中都无法取到等号，只有解法4的答案是正确的.从中还总结利用基本不等式求最值要注意的问题：“一正、二定、三相等”.这样通过错题集，学生自己不断积累错误，加深学生对易错地方的印象，避免错误的再次发生.

又如，学生在求定义域，值域时总漏掉一些函数本身固有的范围，如指数函数，对数函数，三角函数等；在求离心率时会忘记要与椭圆或双曲线本身的范围取交集；当一个集合为某一集合的子集时总是不考虑空集的情况等.这些问题只要平时多积累，考试时就不容易犯错.

错题集是提高学习效率的办法.通过错题集的使用，可以提高思维质量，可以更准确地把握知识点及概念，可以极大地改善粗心的现象，可以迅速地提高学习成绩，有效地进行数学反思.

总之，重视学生错题集的建立是基于学生的思维实际，避免老师全盘灌输，让学生将自己的数学思维方式在错题集上显现出来，让学生自己主动整理，纠错，反思，从而培养学生优良的数学思维品质.