排序原理在不等式证明中的应用

☉宁夏彭阳县第三中学 王伯龙

人教A版数学选修专题4-5《不等式选讲》模块中给我们介绍了柯西不等式与排序不等式，是课标教材中新增加的内容，也是高考中的选考内容.关于柯西不等式的应用倍受青睐，多见于各级各类考试的试题中或公开发表的刊物上，而排序不等式却很难见到，对于这样一个形式简单，结构优美的不等式似乎被人们淡忘，其实它在证明不等式中起到举足轻重的作用.

一、排序不等式及其另一种表示形式

排序不等式（又称排序原理）：设a1≤a2≤…≤an，b1≤b2≤…≤bn为两组实数，c1，c2，…，cn是b1，b2，…，bn的任一排列，则有a1bn+a2bn-1+…+anb1≤a1c1+a2c2+…+ancn≤a1b1+a2b2+…+anbn，即反序和≤乱序和≤顺序和.为了便于研究问题，我们令矩阵

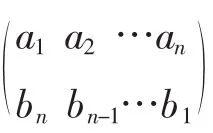
二、排序原理在不等式证明中的应用

1.运用排序原理证明教材中的不等式

例1 已知a，b都是正数，a≠b，求证a3+b3>ab2+a2b（文［1］第41页习题）.

证法1：由对称性，不妨设a>b>0，于是有a2>b2>0，则顺序和为a3+b3，反序和为ab2+a2b，由排序原理得a3+b3>ab2+a2b.

评析：对于这样一个简单优美的不等式，从两个不同的角度出发，用排序原理证明别具独特，回味无穷.

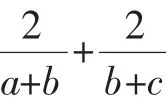
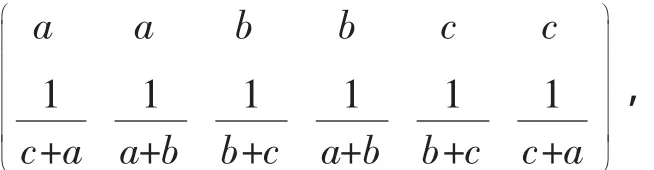
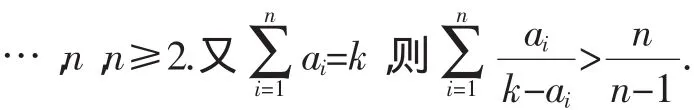
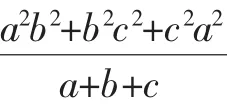
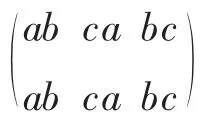
2.运用排序原理证明数学竞赛中的不等式或较难的不等式

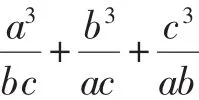
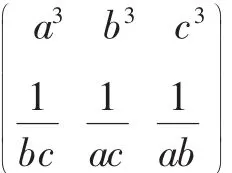
评析：这是一道经久不息的经典赛题，流传至今，证法多达几十种，但用排序原理证明还尚未见到.

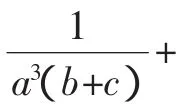
故原不等式成立.

评析：通过合理的排序，使一个原本较难的不等式赛题便可得到轻松愉快的证明，证法新颖独特.

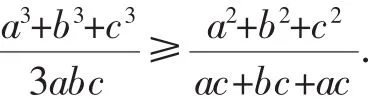
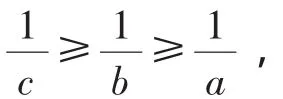
评析：原文的证法是先构造了一个令人十分费解的复杂函数，接着研究函数的单调性，最后再利用单调性进行证明，且证明过程过于复杂，不容易想到，而用排序原理证明则有心旷神怡的感受.

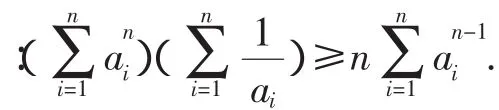
总之，用排序原理证明一些对称不等式问题的关键，是合理的构造出两个数列，进行恰当的排序.然而，这一过程奥妙无穷，需要我们不断地思考、分析、探究、总结经验才能游刃有余.排序原理形式简单，结构优美，为不等式的证明增添了一道靓丽的风景线.

1.普通高中课程标准实验教科书 数学选修4-5不等式选讲［M］.北京：人民教育出版社（A版），2007.