改进BFO算法在函数优化问题上的应用

曹天问，雷秀娟

陕西师范大学 计算机科学学院，西安 710062

改进BFO算法在函数优化问题上的应用

曹天问，雷秀娟

陕西师范大学 计算机科学学院，西安 710062

1 引言

Passino于2002年提出了模拟人类大肠杆菌觅食行为的细菌觅食优化（Bacteria Foraging Optimization，BFO）算法[1]，由于其新颖性吸引了很多学者对它进行研究[2-6]。但是该算法存在早熟收敛的缺陷。Abraham等人[7-8]针对BFO算法的复制操作对算法的收敛性和稳定性的影响进行了理论分析，并得出在复制操作中引入自适应机制能避免算法早熟。但这种理论分析是建立在一定的条件假设上的，只考虑了在一维的连续空间中两个粒子组成的种群进行的复制操作。本文主要是从应用的角度出发，为了进一步提高标准BFO算法的局部搜索能力以及算法的精度以减少早熟现象的发生，对标准BFO算法的趋向、复制和迁徙操作进行了改进和优化，并将改进BFO算法在函数优化问题上进行了仿真实验。

2 标准BFO算法

BFO算法的生物学基础是人类肠道中大肠杆菌在觅食过程中体现出来的智能行为。细菌的觅食行为具有3个典型的模式，分别为趋向性行为、复制行为和迁徙行为[9]。

（1）趋向性操作。大肠杆菌的运动是通过其表面的鞭毛实现的。当鞭毛全部逆时针摆动的时候，大肠杆菌就会向前运动；当鞭毛全部顺时针摆动的时候，它就会减速直至停止并在原地旋转。细菌在觅食的过程中，这两种行为交替进行。设θi(j，k，l)表示个体i当前的位置，其中，j表示第j代趋向性行为，k表示第k代复制行为，l表示第l代迁移行为。BFO算法中方向的调整按照下式进行：

其中，ϕ(j)表示鞭毛摆动后确定的方向，c(i)表示游动步长单位。

（2）复制操作。当细菌完成设定的趋向性操作次数之后，细菌将进行分化，一部分个体由于无法得到足够的食物而被淘汰掉，一部分觅食能力强的个体将得到进行个体繁殖的机会。新复制的个体将取代被淘汰掉的个体。设细菌种群大小为S，在复制过程中，群体中要被淘汰的个体数设为Sr=S/2。首先对群体中的个体按其位置的优劣进行排序，而后将排在最后的Sr个个体删除，剩余的个体进行自身的复制，即复制出与原来的个体一样的新个体，这保证了算法群体规模的稳定。

（3）迁徙操作。细菌群体所依附的生存环境的变化将对其造成很大的影响。这些都很可能使得群体逐渐或者突然发生变化。例如，整个区域内的细菌全部死亡或者部分细菌移动到另外一个全新的环境。迁徙操作就是以一定概率对趋向性操作起到一个促进的作用，因为迁徙操作可能将部分细菌带到离食物源更近的区域。

迁徙操作按照预先给定的概率P发生，如果某个体满足迁徙操作发生的条件，那么将此个体删除，重新生成一个新的个体。这相当于将原来的个体移到了一个新的位置。

BFO算法主要包括3层循环：最外层是迁徙操作循环；中间层是复制操作循环；最内层是趋向性操作循环。

3 改进后的BFO算法

标准BFO算法中细菌个体全部使用相同的最大游动步长，不利于体现细菌个体能力之间的差异性；复制操作采用保留精英的方式对原有细菌进行100%复制，不利于保持种群多样性；迁徙操作以一定概率发生，仅凭概率来决定细菌个体的更换与否，随机性太强，不利于提高算法的全局收索能力。针对以上不足，主要对标准BFO算法作如下改进。

3.1 最大游动步长的改进

趋向操作中最大游动步长改进的理论基础，源于第一个对学习中的强化做出理论分析的心理学家爱德华·桑代克（E L Thordike）的经典效果律和经济学家巴莱多的巴莱多定律。桑代克的效果律中强调了3个重要的行为法则：其一，强化原则。在对相同的环境作出的几种反应中，令人满意的、受到鼓励的行为结果将增加先前行为的力度，并增加未来再次发生此行为的可能性。其二，惩罚原则。不理想的或受到惩罚的行为结果将减少先前行为的力度，并减少未来再次发生此行为的可能性。其三，消退原则。如果行为之后没有任何后果，既没有正性的也没有负性的事后结果，在若干时间后，这种行为将会逐渐消失。巴莱多定律则认为任何一组事物中，最重要的只占其中一小部分，约20%，其余80%的尽管是多数，却是次要的。本文先初始化最大游动步长Ns，Ns根据种群中细菌个体的强化和惩罚进行动态变化，而对细菌个体强化和惩罚的判定条件则依据巴莱多定律，对种群中适应度值排在前20%的精英个体进行强化，即增加其最大游动步长；对适应度值排在后80%的普通个体进行惩罚，即减小其最大游动步长。这就赋予种群中的优秀个体更大搜索空间的特权。由于每次趋向操作时都进行一轮适应度值计算并排序，种群中每一个个体都有得到强化的机会，因此，这种改进增加了种群间个体竞争的激烈程度，有利于提高算法的全局收索能力和收敛速度。

3.2 复制操作的改进

标准BFO算法的复制操作是按照细菌位置的优劣排序，然后把排在后面的一半细菌淘汰掉，剩余的细菌进行自我复制，各自生成一个与自己完全相同的新个体。这使得新个体与原个体具有相同的觅食能力，虽然提高了算法的局部搜索能力，但同时也使种群的多样性受到限制。改进BFO算法的复制操作在淘汰掉排在后面的Sr(Sr=S/2)个个体后，并没有直接将前Sr个个体进行自我复制，而是增加了交叉步骤，将原有种群中的个体两两交叉，然后计算各细菌个体的适应度值，按优劣排序，选择排在前面的Sr个个体取代原种群中被淘汰掉的Sr个个体，保持种群数量不变的同时，也增加了种群个体的多样性。

设pop(S，dim)为原种群，其中S为种群规模，dim为维度。在复制操作中将原有种群中的个体两两交叉，得到新的种群newpop(S，dim)，计算新种群各个体的适应度值，选择新种群前S/2个个体取代原有种群pop(S，dim)中适应度值排在后面的S/2个个体。

3.3 迁徙操作的改进

迁徙操作使BFO算法具有随机搜索的能力，有助于BFO算法保持种群的多样性，减少早熟收敛的现象发生。标准BFO算法的迁徙操作是当细菌个体满足迁徙条件时，随机产生新的个体代替原有个体，而不考虑新生成个体的能力是否优于原有个体。这种迁徙操作随机性大，可能将本来优良的个体灭亡后又随机生成一个相对较差的新个体，影响了算法的收敛速度。改进的BFO算法在迁徙操作的过程中，如果得到的新个体优于当前群体中最差的个体，则用新产生的个体取代当前最差个体进行择优迁徙；否则，保留原来的个体[10]。初始时设i=0，rand()是[0，1]区间上均匀分布的随机数。改进后的迁徙操作能够以更大的概率提高整个群体的平均适应度，为群体增加了优秀的基因，使得算法能够以更大的概率找到全局最优解。

3.4 改进的BFO算法流程

设Nc、Nre、Ned分别是趋向性、复制和迁徙操作的执行次数，j、k、l分别是对这3个操作的计数参数，S为种群数量。改进的BFO算法如下：

步骤1初始化群体，利用评价函数对群体中的各个体进行优劣评估，初始化j=0，k=0，l=0。

步骤2迁徙循环：l=l+1。

步骤3复制循环：k=k+1。

步骤4趋向性循环：j=j+1，对各个个体进行趋向性操作。

步骤5如果j＜Nc，转向步骤4。

步骤6复制操作：将原种群中个体两两交叉，分别选取原种群和交叉后的种群中适应度排在前面的S/2个个体，作为复制后的新种群。

步骤7如果k＜Nre，转向步骤3。

步骤8迁徙操作：如果种群中的某个细菌个体满足迁徙发生的概率，则随机地在解空间生成一个新个体，并计算新个体的适应度值，如果优于当前种群个体中的最差的适应度值，则用新个体替换满足迁徙概率的那一个细菌个体；否则，不予替换。

步骤9如果l＜Ned，则转向步骤2；否则整个算法结束。

表1 用于测试的6个函数

表2 参数设置

4 仿真实验及结果分析

为了显示改进后的BFO算法的高效性，本文选择了在函数优化中经常使用的6个Benchmark函数来体现改进算法的性能，如表1所示。

Rosenbrock函数的全局最优点位于一个平滑且狭长的抛物线山谷内，是一个经典复杂优化函数；Griewank和Rastrigin函数是典型的非线性多模态函数，具有广泛的搜索空间、大量的局部极小点和高大的障碍物，通常被认为是很难处理的复杂多模态问题[11-12]；Shubert函数具有多个全局最小值点，可以很好地检验一个算法跳出局部极值的能力，最小值为-24.062 499；Michalewicz’s有一个全局极小值点，取值近似为-1.801 3。

4.1 参数设置

细菌觅食算法中细菌种群的大小直接影响到细菌寻求最优解的能力，种群数量越小，种群在搜索过程中获得与解有关的信息就越少，种群数量越大，个体初始时分布的区域多，靠近最优解的概率就越大，能避免算法陷入局部极值，但不可避免地增加了算法的计算量[13]。综合算法计算量和搜索精度两方面的考虑，将种群的大小设为100，其他具体的参数设置如表2所示。

改进BFO算法中的最大游动步长4±1是指：趋向操作中的最大游动步长初始值Ns设为4，再在每一次趋向过程中根据细菌个体适应度值的排序情况，将强化的个体的最大游动步长加1，将惩罚的个体的最大游动步长减1。

4.2 实验结果比较分析

4.2.1 单项改进效果分析

Griewank函数是典型的非线性多模态函数，具有广泛的搜索空间，大量的局部极小点和高大的障碍物，通常被认为是很难处理的复杂多模态问题，能够很好地测试算法的性能。因此对于单项改进效果的分析以Griewank函数为例，分别针对3种改进进行独立实验，分析每一种改进的优势。标准BFO算法和改进BFO算法分别对Griewank函数做20次独立实验，并计算其种群平均适应度值。如图1～3，分别为只改进趋向、复制、迁徙后的BFO算法与标准BFO算法的优化效果对比。

如图1，显示了只对趋向操作中最大游动步长进行改进的BFO算法与标准BFO算法在Griewank函数优化上的效果对比，可以看出改进后的算法在对种群中细菌个体的能力差异进行区别后，提高了种群优化解的搜索精度。图2中改进BFO算法在迭代初期就将优化解锁定在0.2附近，而标准BFO算法初始锁定的解区域在0.9周围，这说明改进后的BFO算法在搜索起点上就明显优于标准BFO算法，大大提高了算法的初始搜索精度，为进一步的精确查找奠定了基础。图2中改进BFO算法从第10次迭代开始快速收敛，20代时基本收敛到最优解，说明在复制操作中引入交叉步骤后，增加了种群个体的多样性，大大提升了算法的局部搜索能力和收敛速度。图3可以看出在37次迭代之后，改进迁徙操作后的BFO算法的收敛速度得到明显提升。

图1 趋向改进对比图

图2 复制改进对比图

图3 迁徙改进对比图

就趋向、复制、迁徙3项操作在Griewank函数优化进行独立实验的结果来看，迁徙操作改进后算法在迭代的前中期开始慢慢提高优化解的精度；趋向操作的改进使得算法的搜索精度得到明显提升，使改进后的算法能快速找到最优解；复制操作的改进对算法的性能提升最大，不管是搜索精度还是收敛速度方面都比标准BFO算法有了相当大程度的改进。

4.2.2 综合改进效果分析

上一小节对3项改进操作分别进行了独立实验，分析了各项改进后算法的优化效果。本小节将3项改进综合后，与标准BFO算法进行函数优化效果的对比分析。

由于复制操作中种群交叉操作与遗传算法的交叉操作类似，因此将遗传算法与改进前后的BFO算法一起进行对比分析。对于各测试函数，每种优化算法运行20次求得的结果的最小值(fmin)、最大值(fmax)、平均值(fmean)，平均运行时间(tmean/s)如表3所示。

从表3可以看出改进BFO算法在各个函数上都具有较快的收敛速度和较强的全局搜索能力，尤其是搜索精度得到了很大程度的提升，如Griewank函数的优化精度比标准BFO算法提高了34倍，Rastrigin函数提高了975倍，Sphere函数提高了1 513倍。由于改进的BFO算法增加了更多的操作，使得其运行时间较标准BFO算法要长，但从表3可以看出两者平均运行时间的差距并不明显，相对改进BFO算法在优化效果的强势表现而言，这种平均1 s左右的时间差距是完全可以接受的。另外，改进BFO算法对于Shubert函数的优化比标准BFO算法用时更少。

如图4～9，分别表示遗传算法和改进前后的BFO算法对6个函数进行优化时20次实验的平均种群适应值变化趋势。从图中可以看出，改进后的BFO算法较标准BFO算法收敛更快，优化精度更高，能持续有效地搜索全局最小点，具有很强的挖掘能力。尤其是Griewank和Rastrigin函数，改进BFO算法能快速收敛，展现出了更加卓越的优化性能。改进的BFO算法能够建立全局搜索和局部搜索两者之间更有效的平衡机制。

表3 BFO及其改进算法在Benchmark函数上的优化对比

图4 Sphere函数优化对比图

图5 Rosenbrock函数优化对比图

图6 Griewank函数优化对比图

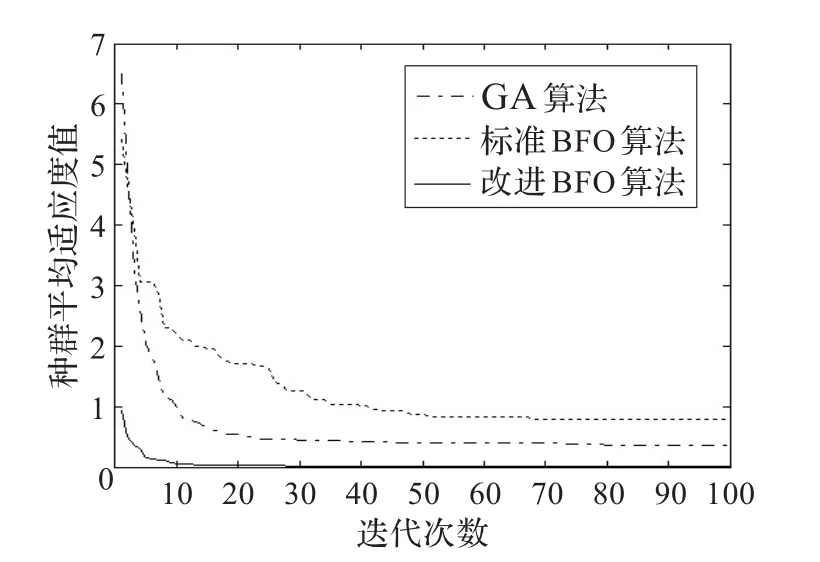
图7 Rastrigin函数优化对比图

图8 Shubert函数优化对比图

图9 Michalewicz’s函数优化对比图

5 结束语

本文主要对标准BFO算法的趋向、复制和迁移操作均进行改进和优化，然后将改进BFO算法在函数优化问题上进行了仿真实验，并对比改进前后的算法在函数优化性能上的表现。

实验结果表明，改进后的BFO算法不管是在单模态还是多模态Benchmark问题上均优于标准BFO算法，在复制操作中增加交叉步骤，将细菌原始种群和交叉后的种群中的优良个体同时保存下来，增加了细菌个体的多样体和种群的进化质量，使细菌更容易找到正确的搜索方向，从而在多模态问题上易越过局部极值而向全局极值收敛。图2表明复制操作的改进对BFO算法的优化性能有了很大提高，这也为BFO算法的进一步研究提供了基础。

[1]Passino K M.Biomimicry of bacterial foraging for distributed optimization and control[J].IEEE Control Systems Magazine，2002，22：52-67.

[2]Tripathy M，Mishra S.Bacteria foraging-based to optimize both real power loss and voltage stability limit[J].IEEE Transactions on Power Systems，2007，22（1）：240-248.

[3]Li M S，Tang W J，Tang W H，et al.Bacterial foraging algorithm with varying population for optimal power flow[C]// Proc of Evol Workshops，2007，4448：32-41.

[4]Abraham A，Biswas A，Dasgupta S，et al.Analysis of reproduction operator in bacterial foraging optimization[C]//Proceedings of the IEEE Congress on Evolutionary Computation（CEC 2008），2008：1476-1483.

[5]Lei Xiujuan，Wu Shuang，Ge Liang，et al.Clustering and overlapping modules detection in PPI network based on IBFO[J]. Proteomics，2013，13（2）：278-290.

[6]Kim D H，Abraham A，Cho J H.A hybrid genetic algorithm and bacterial foraging approach for global optimization[J]. Information Sciences，2007，177（18）：3918-3937.

[7]Das S，Biswas A，Dasgupta S，et al.Bcterial foraging optimization algorithm：theoretical foundations，analysis，and applications[J].Foundations of Comput Intel，2009，3：23-55.

[8]Biswas A，Das S，Dasgupta S，et al.Stability analysis of the reproduction operator in bacterial foraging optimization[C]// Proceedings of the IEEE/ACM International Conference on Soft Computing as Transdisciplinary Science and Technology（CSTST 2008），Paris，France，2008：568-575.

[9]周雅兰.细菌觅食优化算法的研究与应用[J].计算机工程与应用，2010，46（20）：16-21.

[10]梁艳春，吴春国，时小虎，等.群智能优化算法理论与应用[M].北京：科学出版社，2009.

[11]雷秀娟，付阿利，孙晶晶.改进PSO算法的性能分析与研究[J].计算机应用研究，2010，27（2）：453-458.

[12]雷秀娟.群智能优化算法及其应用[M].北京：科学出版社，2012.

[13]杨大炼，李学军，蒋玲莉.一种细菌觅食算法的改进及其应用[J].计算机工程与应用，2012，48（13）：31-34.

CAO Tianwen,LEI Xiujuan

College of Computer Science,Shanxi Normal University,Xi’an 710062,China

The principle of the Bacterial Foraging Optimization（BFO）algorithm as well as the current research status is analyzed firstly,then the standard BFO algorithm is improved to overcome its insufficiency mainly based on the classic effect law of psychologist Edward Thorndike grams（E L Thordike）and the Pareto’s law of economist Pareto.The experimental results on Benchmark function optimization problems show that the improved BFO algorithm has the higher searching performance and convergence rate than the standard BFO algorithm.

Bacteria Foraging Optimization（BFO）;trends;the maximum swim step;replication;preferential migration

分析了细菌觅食优化（BFO）算法的原理以及当前的研究状况，主要根据心理学家爱德华·桑代克（E L Thordike）的经典效果律和经济学家巴莱多的巴莱多定律等对标准BFO算法存在的不足进行改进；将改进后的BFO算法在函数优化问题上进行仿真实验，实验结果表明改进后的BFO算法比标准BFO算法具有更快的收敛速度和更强的搜索性能。

细菌觅食优化（BFO）；趋向；最大游动步长；复制；择优迁徙

A

TP301

10.3778/j.issn.1002-8331.1212-0095

CAO Tianwen,LEI Xiujuan.Application of improved Bacteria Foraging Optimization algorithm on function optimization.Computer Engineering and Applications,2013,49（13）：175-179.

国家自然科学青年基金（No.61100164，No.61173190）；教育部留学回国人员科研启动基金（教外司留[2012]1707号）；陕西省2010年自然科学基础研究计划青年基金（No.2010JQ8034）。

曹天问（1989—），男，硕士研究生，主要研究方向为细菌觅食优化；雷秀娟（1975—），通讯作者，女，博士，教授，主要研究领域为智能计算与智能优化，生物信息计算。E-mail：xjlei168@163.com

2012-12-10

2013-03-04

1002-8331（2013）13-0175-05