上市公司股权价值评估的实物期权定价模型——兼论亏损类上市公司股权价值评估

■应尚军 潘向阳 何荣

公司能够上市一般说明其盈利能力较强或者成长性较好，然而在我国，不少公司上市后却出现了亏损。截至2012年4月27日，A股共有2349家上市公司披露年报，其中亏损家数占到153家，亏损比例为6.51%，亏损金额合计达到423亿元；2011年亏损榜前10大上市公司合计亏损220亿元，不仅远高于2010年亏损榜前10大上市公司合计88.7亿元的亏损总额，甚至超过2010年全部亏损上市公司170亿元的亏损总额①来源：上海证券报文章《亏损广度深度同步放大，谁是A股“亏损王”》。亏损类上市公司的股权自由现金流量一般为负，如果亏损一直持续，其未来现金流也为负。根据财务理论[1]，股权自由现金流的现值即是股票价值，如果市场有效，则亏损类上市公司的股票价格应该为负。但是，现实的观察结果却是某些亏损股却呈现出了相当好的涨势。这类亏损股一般以重组概念股出现，它们对投资者有很大的吸引力，因为其中可能拥有价值较高的期权。

这就需要探寻一种新的评估方法，要求不但适用于一般上市公司的股权价值评估，而且还适用于亏损类上市公司的股权价值评估。科学的评估方法认为上市公司的股权价值不仅包含可预测的现金流现值，而且还包含可能存在的期权价值，实践中可以考虑将这两者相加作为上市公司股权的价值。然而从广义上看，可以用另一种方法替代，以避免股权现金流为负数的情况。其实，上市公司的股权可被看作是一个标的资产为公司整体资产、约定价格为债务现值的看涨期权[2]。因此，可以将期权定价理论应用于评估上市公司的股权价值。在期权定价理论中，将公司股权、不动产、投资项目、无形资产等非金融资产价值用期权价值来表现的方法称为实物期权定价方法[3]。在国外，已有多项研究成果介绍了如何将实物期权定价方法应用于各类实物资产的定价，譬如对电厂和输电线路的定价[4]、对R&D项目的定价[5]、对产品族结构的定价[6]、对公司外部气候影响的定价[7]，也有研究成果涉及到对实物期权定价方法的深化，譬如，用离散时间、动态规划、决策树等分析方法与实物期权定价方法结合起来[8]，用模糊数学分析方法与实物期权定价方法结合起来[9]。在国内，近年来也出现了许多关于实物期权的研究成果，尤其是在并购活动中目标企业价值评估方面[10～17]，国内学者普遍认为，并购价值等于标的企业自身价值加上并购附加值，而附加值主要体现在对于并购方的增长期权和放弃期权。在实物期权定价方法上，国内学者也在寻求改进，除了在高科技企业中应用模糊期权定价模型外[18]，也探寻了灰色系统理论与实物期权定价方法的结合，并将其应用在水电企业价值评估中[19]。虽然实物期权定价方法得到了广泛的应用，但是它在公司股权尤其是亏损类公司股权的价值评估中的应用却不多见。

根据市场现状及理论研究现状，本文将以上市公司股权为评估对象构建实物期权定价模型，并对该模型如何在亏损类上市公司股权价值评估中的应用作出阐述。

一、实物期权定价模型的理论基础

1.Black-Scholes模型

Black与Scholes所创立的期权定价模型表述如下[20]：

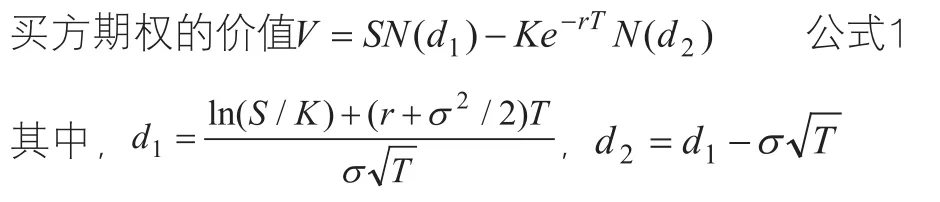
S：标的资产的当前价格；K：期权的约定价格；T：期权的有效期；r：无风险利率；：标的资产价格对数收益率的波动率；N(X)：标准正态分布下变量小于X的累计概率。

2.遗传算法

遗传算法是一类借鉴生物自然选择和自然遗传机制的随机搜索算法，由美国学者J.Holland教授[21]提出，其主要特点是群体搜索策略和群体中个体之间的信息交换，搜索不依赖于梯度信息[22]。其中标准遗传算法的基本流程如图1所示，具体步骤描述如下[23]：

步骤1：产生初始群体。群体中的个体为用二进制串来表示的染色体，一个二进制串就是优化问题可行域内的一个解；

步骤2：计算适应度值。用目标函数作为适应度函数来模拟个体对生存环境的适应性，适应度大的个体有更大几率被选择复制到下一代；

步骤3：执行选择、交叉、变异操作，产生新一代群体，群体规模保持不变；

步骤4：计算新一代群体中个体的适应度值；

步骤5：如果满足结束条件则停止，否则转到步骤3进行循环。

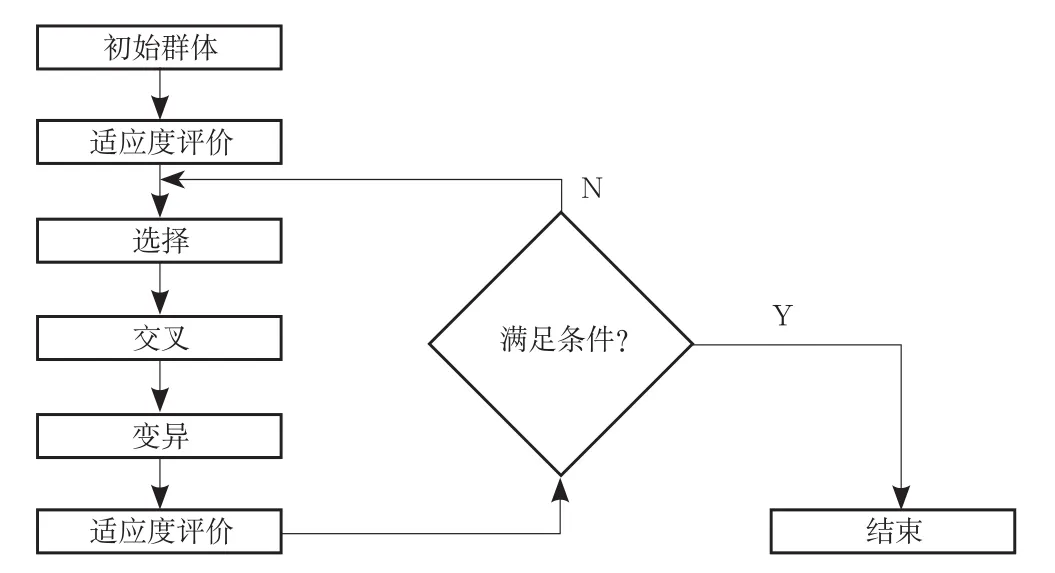
图1 标准遗传算法

二、实物期权定价模型的构建

采用实物期权定价模型评估上市公司股权价值的基本思路是将公司的股权作为期权进行评估。被视为期权的上市公司股权如果被行权，则意味着股东付出与公司债务账面价值相等的资金数额后可以得到公司的全部资产。因此，上市公司股权的价值相当于公司资产的买方期权，可以借鉴Black-Scholes模型的思路构建以公司股权为评估对象的实物期权定价模型，这种方法对于亏损类上市公司来说，尤其具有实际意义。

实物期权定价模型的构建，关键在于五个参数的确定，它们是：无风险利率、标的资产价格、约定价格、标的资产波动率、行权期。这一点与以金融资产为研究对象的Black-Scholes模型是一致的，实物期权与金融期权的不同之处在于应用对象的不同。

1.无风险利率的确定

在期权定价公式中，会涉及计算与特定时间相对应的无风险利率的问题，因为标的资产的约定价格需要以无风险利率为回报率被折现到当前时点。在我国，还未发现行之有效的用于计算无风险利率的利率期限结构实证分析模型，在构建上市公司股权的实物期权定价模型之前，有必要将不同期限的国债复合回报率拟合出来，并将其作为计算无风险利率的基础。根据任姝仪、杨丰梅、周荣喜[24]的研究成果，利率期限结构Nelson-Siegel族模型中的五因子参数模型（FF模型）与我国国债市场的实际数据有着较高的拟合度，FF模型如下：

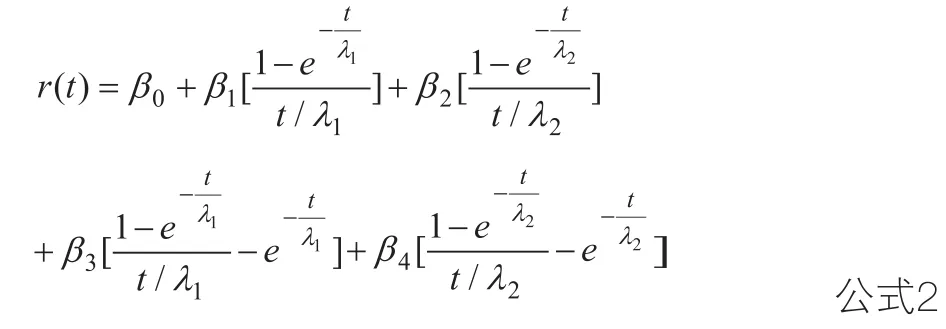
根据中国国债市场的实际数据用遗传算法进行拟合，F模型可具体表达为：

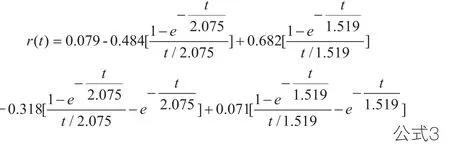
2.标的资产价格的确定

标的资产价格即上市公司的整体资产价格，该价格可以通过三种方法计算得到：一是假设公司所有的债务与股权都上市交易，将债务市值与股权市值加总得到公司整体资产价格；二是通过期望自由现金流折现求得公司整体资产价格；三是资产基础法。Copeland & Antikarov[3]认为，对于不可交易的实物资产可以直接将该资产的账面价值作为资产价格，且当该不可交易的实物资产是公司整体资产时，存在交易假设下该实物资产市场价值的无偏估计，据此推测，该无偏估计就是公司整体资产的账面价值。

在我国，由于大多数上市公司的债务并不上市交易且股权市值也往往偏离实际价值，因此无法采用上述第一种方法；第二种方法适合于企业自由现金流为正数的上市公司；第三种方法在可操作性上没有任何问题，但是评估成本较高。

对于亏损类上市公司来说，根据Copeland & Antikarov的论述，可以公司整体资产的占面价值作为标的资产价格。

3.约定价格的确定

实物期权的约定价格是股东行权的成本，而且往往是这种情况：约定价格不是一次性支付的，行权期也要依据财务经营状况及外部环境进行灵活选择。在现代企业制度下，期权的行权价格是确定的，即是公司债务价值。如果公司债务均来源于对外发行债券，可以根据对应的债券评级用收益法求得其现值。在公司债不发达及债券评级制度不完善的情况下，可以采用公司债务的账面价值作为约定价格。

4.标的资产波动率

本文的标的资产波动率即公司价格的方差，如果上市公司的股票和债务都上市交易，则可用以下公式计算公司价格的方差：

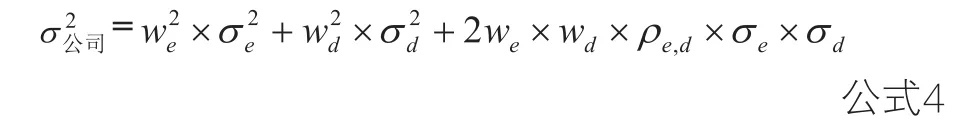
在上式中，为公司股票价格的方差，为公司债务价格的方差，分别为股票和债务价值占公司资产价值的比重，为公司股票价格和债务价格的相关系数。如果公司债务没有上市交易，则用类似风险等级的上市债券和类似公司的股权债券关系来分别估算

在我国，由于公司债市场不成熟，即便能找到其市场价格，波动范围也较窄，因此，公司债务价格相对于股票价格是稳定的，可以用股票价格的波动率替代公司整体资产价格的波动率。

5.行权期的确定

公司股东一旦行权则意味着公司面临清算。当公司有红利产生时，在市场有效的假设前提下，股东们不关心红利何时发放以及红利支付的比率，因为即便有红利支付，也是支付给股东自己，他们的利益不会发生变化。因此，当公司前景不佳或股东有解散公司意图时，不会因为红利的支付影响他们做出清算决定的时间。一般情况下，只要公司能正常经营，股东不会谋求清算，因为从公式1看，行权期越长，公司股权的价值越高。

对于亏损类公司来说，都存在被股东行权的可能，而且行权的时点一般都发生在公司债务的到期日。事实上，绝大多数公司都不止一笔债务，而且多数要付息，要把这些债务折合成一笔零息债券。实践中有一种做法，即将利息支付和到期时间本金支付按照占面值的比重计算出一个加权平均债券持续期，这个持续期就是行权期。

三、实证分析

本文以亏损类上市公司作为实证分析对象。

1.样本选择

为满足期权定价公式本身的假设条件以及评估的有效性和可操作性，实证应用中应排除以下两类亏损类上市公司：一是长期处于亏损状态的上市公司。亏损类上市公司质量良莠不齐、亏损原因不一而足。一些历史悠久的亏损类上市公司由于长期包袱的拖累，公司近乎丧失自主经营能力，财务数据已经不能有效地反映其真实盈利潜力，这样等待破产的公司应采用清算法来评估其公司股权价值。二是仅具壳资源的亏损类上市公司。壳资源公司一般是具有市值比较小、主营业务完全停止并剥离、没有复杂债务债权等特征的上市公司。壳资源上市公司极有可能被一些不具备上市资格的公司并购，以达到间接上市的目的。这种并购行为使得本来没有任何价值的垃圾股票由于壳的意义而产生股价的非理性波动，此时应用期权定价公式评估出的股权价值已失去实际意义。

根据以上要求，本文选取某上市公司A作为实证分析案例，以探讨实物期权定价方法在亏损类上市公司股权价值评估中的应用。假设评估基准日为2011年12月31日。

2.样本描述

公司A是一家以商业地产开发和商业经营为主的企业，公司经营范围包括商品零售、经营房地产、代购、代销、种植、销售林木、进出口业务。2011年归属于上市公司的净利润为－123,774,612.23元，比2010年下降27.71%，公司已经连续两年亏损。公司A发生亏损的主要原因是公司某项目仍处于投入期，没能产生收益，随着公司遗留问题的清理和主营业务的逐渐调整恢复，公司步入良性发展轨道的可能性比较高。因此，公司A的情况符合本文应用实物期权定价方法评估的亏损公司范围。

3.参数估计

(1) 标的资产价格：采用公司A合并资产负债表中的总资产数值作为标的资产价格的估计值，其值为1,537,761,372.58元。

(2) 约定价格：采用公司A合并资产负债表中的负债总额作为约定价格的估计值，其值为1,906,598,811.47元。

(3) 标的资产波动率：取公司A的上市股票自1996年7月8日上市起至2011年12月31日共计761个周收益率，计算得出周收益波动率为8.38%，再乘以年均交易周数的平方根，即得出年股票收益波动率为59.24%。

(4) 行权期根据前文关于亏损类上市公司的行权期的计算方法，得出公司A各类债务的剩余期限或加权剩余期限如表1所示。

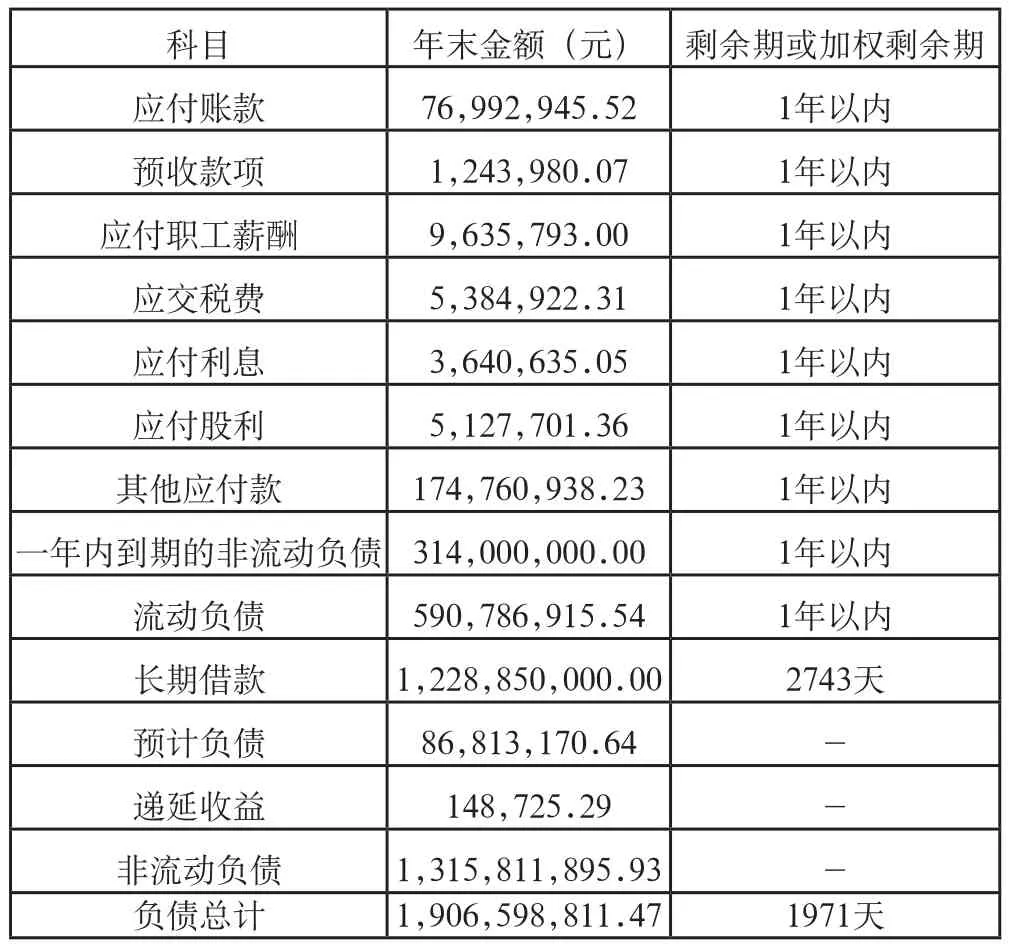
表1 公司A各类债务的剩余期限或加权剩余期限

其中，长期借款的加权剩余期限由4笔长期借款的剩余期加权计算得出。如果以年为单位，则公司A负债总额的剩余期为：1971/365=5.4（年），该期限即为公司A股权价值评估的行权期。

4.评估结果

先将t=5.4代入式中，得到无风险利率为0.021209；然后在MAT LAB软件命令窗口中输入如下指令：price=1,537,761,372.58；strike=1,906,598,811.47；volatility=0.5924；time=5.4; rate=0.021209；V=blsprice(price, strike, rate, time, volatility)。从而得出公司A的股权价值V=744270000元。

四、研究结论

通过上述研究，本文得出以下结论：

1. 上市公司股权价值评估的实物期权定价模型，实质是将Black-Scholes模型中对应的标的资产从金融资产变为上市公司整体资产。运用Black-Scholes公式计算公司股权价值所需的五个参数可以通过一定的方式得到，从而使得期权定价方法在上市公司股权价值评估中的应用成为可能。

2. 对于有一定规模的、有潜力的、暂时处于亏损状态的上市公司，标的资产价格一般用公司总资产的账面价值来表示，而且从谨慎原则上考虑，行权期一般取公司债务未能获得展期条件下的加权平均零息债务的剩余期。

[1]斯蒂芬A.罗斯,伦道夫W.威斯特菲尔德,杰弗利F.杰富.公司理财(第9版)[M].吴世农,王志强(译).北京:机械工业出版社,2011.

[2]John C. Hull. Options, Futures and Other Derivatives [M]. Pearson Education Group, 2007.

[3]Copeland, T. and V. Antikarov. Real Options[M]. New York:Texere LLC, 2001.

[4]Ewa Broszkiewicz-Suwaj. Electricity real options valuation[J]. Acta Physica Polonica B, 2006, 37(11):2955-2965.

[5]A. Cagri Tolga. Fuzzy multicriteria R&D project selection with a real options valuation model[J]. Journal of Intelligent & Fuzzy Systems, 2008, (19):359-371.

[6]Jianxin Jiao, Arun Kumar, Ching Moi Lim. Flexibility valuation of product family architecture: a real-option approach[J]. Int J Adv Manuf Technol, 2006, (30): 1-9.

[7]Emily Tyler, Richard Chivaka. The use of real 0ptions valuation methodology in enhancing the understanding of the impact of climate change on companies[J]. Business Strategy and the Environment,2011, (20):55-70.

[8]Luiz E. Brandao, James S. Dyer. Decision analysis and real options: a discrete time approach to real option valuation[C]. Annals of Operations Research, 2005, (135):21-39.

[9]Shin-Yun Wang. A fuzzy real option valuation approach to capital budgeting under uncertainty environment[J]. International Journal of Information Technology & Decision Making, 2010, 9(5):695-713.

[10]侯汉坡,邱菀华.基于实物期权的并购企业价值评估模型与应用[J].系统工程理论方法应用,2005,14(1):11-17.

[11]赵敏,唐元虎,李湛.基于实物期权的科技创业企业并购价值评估研究[J].管理科学,2005,18(5):27-30.

[12]殷仲民,杨莎.基于实物期权方法的并购中目标企业价值评估[J].经济管理·新管理,2005,(16):32-38.

[13]文海涛.基于实物期权理论的企业并购价值评估[J].生产力研究,2010,(7):209-211.

[14]方晓成,李姚矿,龙丹.基于增长期权的并购目标企业价值评估[J].价值工程,2008,(5):52-55.

[15]张燕,吴伟容.期权定价法在房地产行业并购目标企业价值评估中的应用[J].中国证券期货,2012,(5):274-275.

[16]齐安甜,张维.实物期权框架下的企业并购价值评估[J].系统工程学报,2004,19(4):203-207.

[17]白光泽,刘鸣镝,苏宁.实物期权评估法在企业并购中的应用[J].经济研究导刊,2011,(13):101-103.

[18]李姚矿,熊兴华,夏琼,张行宇.风险投资中企业价值评估的模糊期权定价模型[J].合肥工业大学学报(自然科学版),2008,31(9):1494-1497.

[19]王建辉,陈祥义.实物期权理论和灰色系统理论在水电企业价值评估中的应用探讨[J].中国资产评估,2011,(10):36-40.

[20]BlackF,ScholesM,Thepricingofoptionsandcorporateliabilities[J].JournalofPoliticalEconomy,1973,81(3):637-654.

[21]HollandJH.AdaptationinNaturalandArtificialSystems[M].Cambridge,MA:MITPress,1992.

[22]陈国良,王煦法,庄镇泉,等.遗传算法及其应用[M].北京:人民邮电出版社,1996.

[23]金菊良,丁晶.水资源系统工程[M].四川:四川科学技术出版社,2002.

[24]任姝仪,杨丰梅,周荣喜.中国国债利率期限结构Nelson-Siegel族模型实证比较[J].系统工程,2011,29(11):30-34.

[25]刘卫国.MATLAB程序设计与应用[M].北京:高等教育出版社,2006.

《晨曦》 赵鹏