关于对权证评估的应用研究

■李忠余 王慧

一、权证内涵

（一）权证的含义

权证的英文名称为Warrant，是指一种具有到期日及行使价或其他执行条件的金融衍生工具。根据美国证券交易所的定义，Warrant是指一种以约定的价格和时间（或在权证协议里列明的一系列期间内分别以相应价格）购买或者出售标的资产的期权。根据《深圳证券交易所权证管理暂行办法》，权证是指标的证券发行人或其以外的第三人（以下简称发行人）发行的，约定持有人在规定期间内或特定到期日，有权按约定价格向发行人购买或出售标的证券，或以现金结算方式收取结算差价的有价证券。

权证本质上为一权利契约，投资人于支付权利金购得权证后，有权于某一特定期间或到期日，按约定的价格（行使价）认购或沽出一定数量的标的证券。权证的交易实属一种期权的买卖。与所有期权一样，权证持有人在支付权利金后获得权利，是否行使由权证持有人自主决定。

（二）权证的分类

根据不同的分类标准，权证可分为以下几种：

1. 按交易方式可分为认购权证和认沽权证。认购权证持有人有权按约定价格在特定期限内或到期日向发行人买入标的证券，认沽权证持有人则有权卖出标的证券。

2. 按权证的发行人可分为股本权证和备兑权证。股本权证一般是由标的证券发行人发行，行权会使股份增加；备兑权证一般是由标的证券发行人以外的第三方发行，行权后不会增加股本。

3. 按行权时间可分为欧式权证和美式权证，美式权证持有人在权证到期日前的任何交易时间都能行使其权利，欧式权证持有人只能于权证到期日当日行使其权利。

4. 按结算方式可分为证券给付结算型权证和现金结算型权证。证券给付结算方式，其标的证券的所有权发生转移；现金结算方式，按照结算差价进行现金兑付，标的证券所有权不发生转移。

5. 按权证行使价格是否高于标的证券价格，可分为价内权证、价平权证和价外权证。

（三）权证的基本要素

从权证的设计来看，其一般包含以下几个要素：发行人、看涨和看跌权证、到期日、执行方式、交割方式、认股价（执行价）、权证价格、认购比率、杠杆比率等。

（四）权证价值及其影响因素

权证的价值包括内在价值和时间价值，影响其价值的因素主要有：标的证券市价、标的证券波动率、行权价格、行权比例、权证的有效期限、红利以及无风险利率七种因素。

二、权证的评估方法

权证本质上是一种期权，一般来说，期权定价的常用模型有三种，分别是Black－Scholes模型、二叉树（Binomial Trees）模型和蒙特卡罗（Monte Carlo）模拟，下面分别进行简单阐述。

（一）Black－Scholes模型

Black－Scholes模型是一种解析模型，在给定输入参数的情况下能够得到确定的解析解，但其建立在极其严格的假设条件上，包括：市场无摩擦，即无交易成本，无税收；证券允许卖空；标的证券价格的波动性σ为一已知的常数；在衍生证券的存续期内不支付红利，标的证券价格变动是连续性的；市场上不存在无风险的套利机会；存在一个固定的、无风险的利率r；标的证券的价格符合几何布朗运动。

该模型的基本表达式为：

欧式看涨期权

欧式看跌期权

N（）表示正态分布下的累计概率。

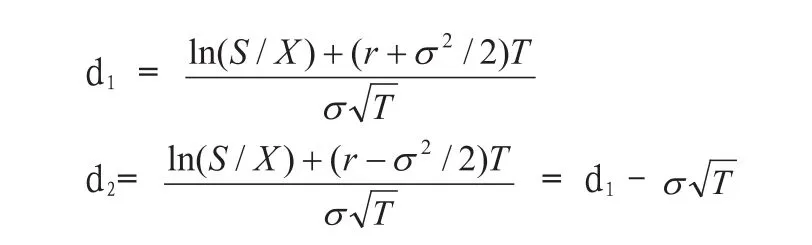
式中：S：标的证券市价；X：执行价格；r：无风险利率；T：有效期；σ：标的证券波动率。

（二）二叉树（Binomial Trees）模型

二叉树模型是用离散的随机游走模拟资产价格连续变动的可能路径，并利用二叉树状图求出到期日的资产价格，从而计算出当前期权价格。它假设标的资产在下一个时间点的价格只有上升和下降两种可能结果，然后通过分叉的树枝来形象描述标的资产和期权价格的演进历程。

假设标的资产价格的运动是由大量的小幅度二值运动构成，在每个小的时间间隔内资产的价格只有上升或者下降两种运动的可能，上升或下降的概率呈二项分布状。根据风险中性假设，单期二叉树模型可表示为：

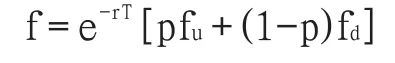
式中：f：期权现值；r：无风险概率；p：上升风险中性概率，u： 下降风险中性概率；fu：上涨期权；fd：下降期权；T：期权有效期。

同样，可以得到多期二叉树模型：

1.欧式看涨期权二叉树模型：

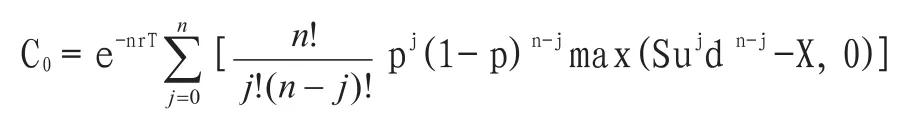
2.欧式看跌期权二叉树模型：

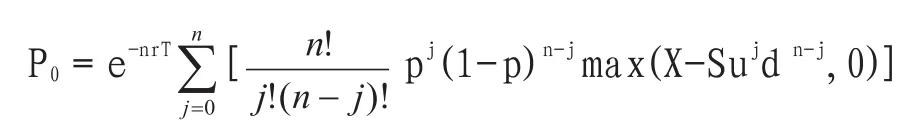
式中：n：期数；X：执行价格；Sujdn-j：标的证券期后价格。

（三）蒙特卡洛（Monte Carlo）模拟

蒙特卡罗模拟是一种通过模拟标的资产价格随机运动路径而计算出期权期望值的数值算法，作为金融衍生证券定价的一种有效数值方法之一，近年来得到了不断的应用和发展。它在每次的模拟环境中都会产生一个价格，其与真实价格的误差会随着模拟次数的增加而逐渐缩小。

假定在风险中性世界，标的资产价格服从以下过程：。式中：dz为一个维纳过程，为了模拟标的资产价格的路径，可以将期权的期限分割成N个长度为Δt的小区间，上式可近似为：，式中ε是标准正态分布中的抽样。实际中对lnS抽样比对S抽样更为准确，上式又可变为：，此式可用于计算T时刻衍生产品的价格。

三、权证评估实例

下面结合一个评估案例，按照上述三种方法分别对被评估权证进行评估。

国内某公司欲合并会计报表，要对其在香港上市的某一控股子公司的可辨认净资产进行公允价值评估，其中评估范围包含有该香港上市公司发行的权证，该公司于2009年10月19日，向独立第三方发行了6000万份认股权证，每份面值港币0.02元，期限为3年，每份认股权证附有按每股港币0.62元认购一股普通股的权利。尚未转换之任何认股证的权利将于2012年10月18日届满。评估基准日为2011年12月31日，截至评估基准日，该权证数量尚有5000万份，现需评估该权证的市场价格。经查阅该权证的发行协议、访谈及其他资料，认为该权证是欧式看涨期权。

（一）Black－Scholes模型评估

用Black－Scholes模型评估，主要是确定相关参数：

1. 标的资产价格（S）的确定。可通过香港交易所网站可查其基准日市价为1.8港元。

2. 波动率（σ）的计算。，其中，为第i日市价，笔者计算了2011年下半年的日波动率 ，该年实际交易日为260日，

3. 无风险收益率（r）的计算。无风险收益率是指不存在违约风险的收益率，可以参照剩余期限与期权行权期限相同或者相近的国债或政府债到期收益率确定。笔者选取香港金融管理局发布的与被估对象剩余期限相近的香港外汇债券收益率作为无风险收益率，即：r=0.2345%。

4. 期权期限（T）的确定。从评估基准日到权利届满日2012年10月18日，还有0.8年。

笔者通过Excel函数进行计算，在D1表格中输入(LN(B1/B4)+(B3－B6+B2^2/2)＊B5)/(B2＊SQRT(B5))，在D2格中输入B9－B2＊SQRT(B5)，在D3格中输入NORMSDIST(B9)，在D4格中输入=NORMSDIST(B10)，在B6格中输入B1＊EXP(-B6＊B5)＊B11－B4＊EXP(-B3＊B5)＊B12，见下表：

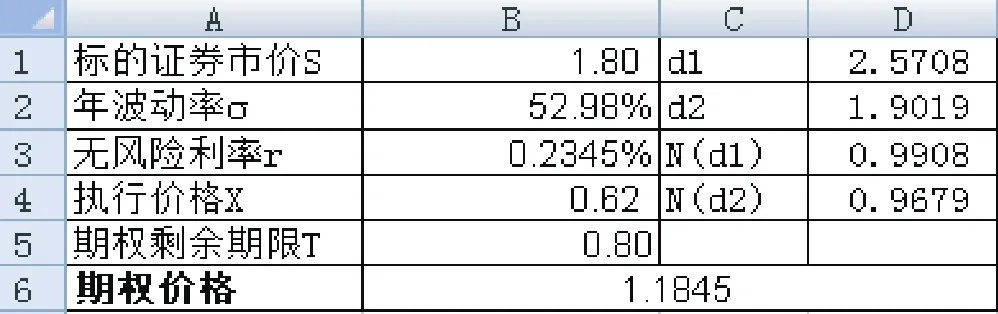
则一份权证的评估价为1.1845港元。

（二）二叉树（Binomial Trees）模型评估

笔者通过Excel进行二叉树计算，将期权剩余期限均分为200个时间间隔，利用多期二叉树公式来计算。在下表中输入相应参数，在D6格中输入B10/B11，在D7格中输入EXP(B9＊SQRT(D6))，D8格中输入1/D7，D9格中输入EXP(B8＊D6) ，D10格中输入(D9－D8)/(D7－D8) ，D11格中输入1-D10。见下表：

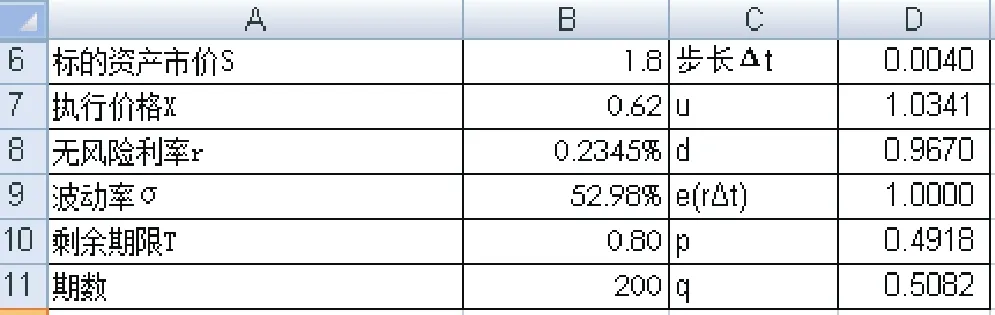
在A407中输入(D10＊B405+D11＊B409)＊EXP(-B8＊D6)，在B405中输入(D10＊C403+D11＊C407)＊EXP(-B8＊D6)，在B409中输入(D10＊C407+D11＊C411)＊EXP(-B8＊D6)，依次类推，一直到第200步。计算值见下表：

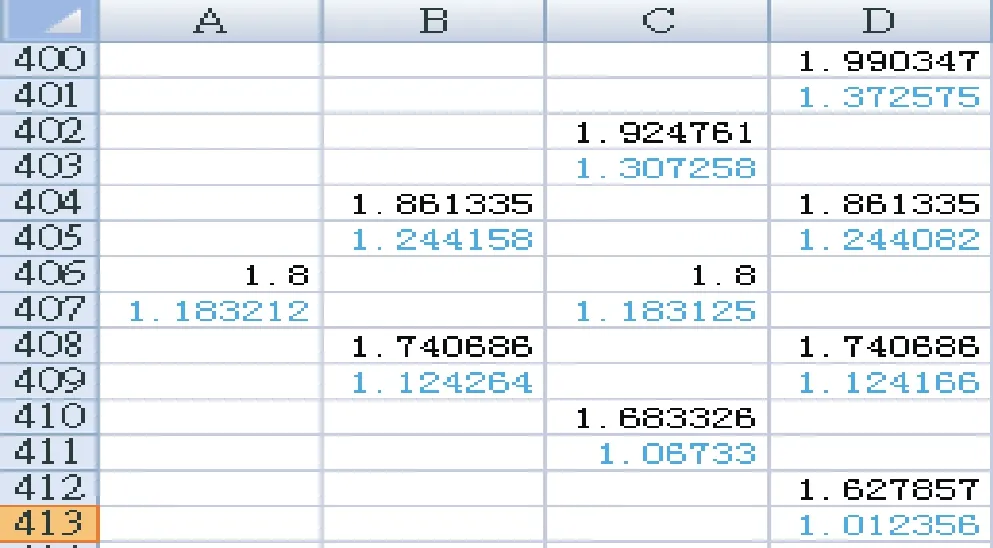
其中第4步至第200步计算表省略，则二叉树计算的一份权证价格为1.1832港元。

（三）蒙特卡洛（Monte Carlo）模拟评估

笔者通过Excel进行蒙特卡洛模拟，在I2至I20000表格中输入$B$2＊EXP(($B$4-$B$5＊$B$5/2)＊$B$6+$B$5＊NORMSINV(RAND())＊SQRT($B$6))来模拟到期价格，分别模拟了1000次、5000次、10000次、15000次和20000次，并分别求出相应次数期权的平均值和标准差，结果如上表。

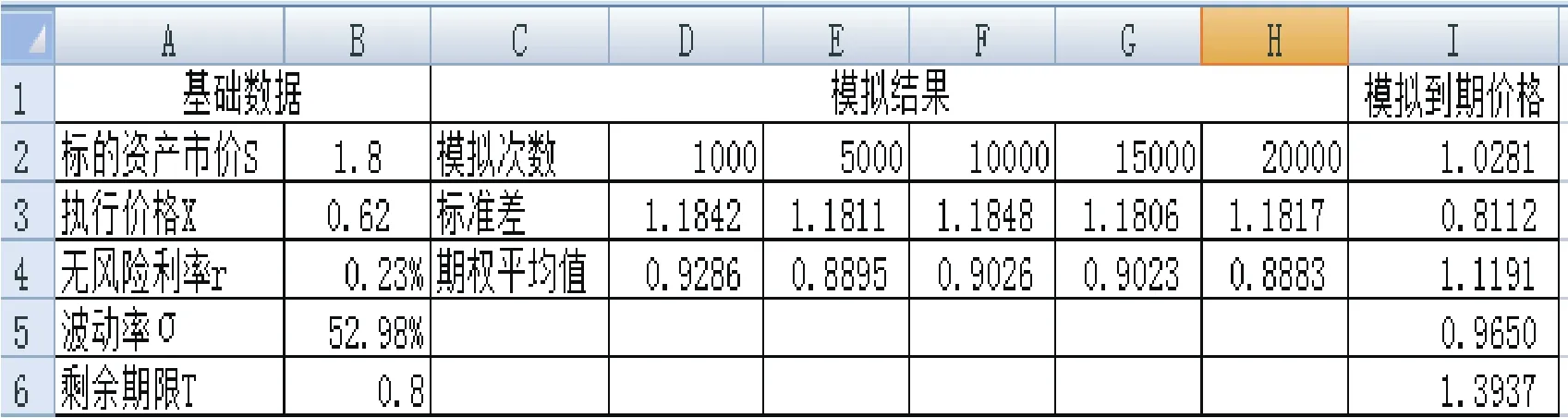
笔者选取模拟20000次的期权平均值为本次单份权证的评估价，即一份权证评估价为1.1817港元。

通过上述三种方法，可以看出其计算结果非常接近，根据具体情况，可以选取三种结果的平均值或某一种方法的结果作为最终评估结果。但上述三种方法也有具体的适用范围，最基本的区别在于三种方法都可对欧式期权进行计算，但Black－Scholes模型和蒙特卡洛（Monte Carlo）模拟很难对美式期权进行计算，在实际项目中要根据权证的具体情况选取合适的方法。

《双生》 赵静

[1]中国资产评估协会.实物期权评估指导意见（试行）.2011.

[2]（美）麦克米伦.麦克米伦谈期权.机械工业出版社,2011年9月.

[3]（加）赫尔.期权、期货和其他衍生品.清华大学出版社,2011年7月.

[4]宋浩平.期货及期权投资实务.首都经济贸易大学出版社,2011年9月.

[5]（英）海厄姆.实用金融期权估值导论(英文版).人民邮电出版社, 2009年8月.

[6]陈晗.金融衍生品：演进路径与监管措施.中国金融出版社, 2008年6月.