等级记分模型下几种等值方法的比较研究

王菲 任杰 张泉慧 曹文静

1 引言

等值是指调整不同版本平行测验间的分数，使之统一在一个量表上、实现分数互换的过程；在保证测验的公平性和测验分数的可比性方面具有重要的作用，是建设题库、开发计算机化测验和适应性测验过程中的关键步骤。我国是一个考试大国，数量繁多的考试被广泛应用于社会的各个领域。然而，我国的大部分测验和考试却没有实现等值，等值研究现阶段仍是我国测量研究中一个比较薄弱的环节，尽快实现等值是国内许多考试所共同面临的重要任务；少数经过等值的考试中，大多只限于对二级记分题目的等值，对多级记分题目的等值研究更是少之又少。

随着实践中教育测验评价形式的丰富，多种多样的考试题型应运而生，对我们的等值工作提出了新的要求。许多考试中不仅包含有“0，1”记分的题目，还出现了正确答案为多个选项，按照答对数目赋分的多级记分题目。该研究正是针对包含多级记分题目的国内某大型语言类考试，选择了目前普遍应用于多级记分等值的等级反应模型，使用同时校准法、固定共同题参数法以及链接独立校准法中的平均数标准差方法、平均数平均数方法、Haebara法和Stocking-Lord法六种方法进行等值，在各试卷版本之间利用共同题进行连接，通过比较六种方法的跨样本一致性，并以此作为评价等值效果的标准，为该考试选择最优的等值方法。

2 实验设计

研究使用某语言类大型考试2011年正式考试的3份试卷作为实验材料，其中1份为标杆卷，另外2份待等值的试卷分别称为新卷1、新卷2。等值以分测验为单位进行，进行等值的包括其中两个分测验，分测验一包含四种题型，共28道题，满分35分；分测验二包含三种题型，共25道题，满分35分。该考试不同于一般“0，1”记分的考试，区别在于其记分方式不仅有“0，1”记分的题目，还包括“0，2”、“0，0.5”这样的二级记分题目，而且出现了“0，0.5，1”这样的多级记分题目。

2.1 等值方法

等值的过程涉及等值数据的收集和等值数据的处理两个方面。该考试采用非等组锚题设计（Non-Equivalent groups with Anchor Test，NEAT）收集数据，也称为共同题设计或锚题设计，即两组水平不一样的考生分别参加两个不同考卷的测验，这两份试卷中包含一部分相同的题目。

在最常用的NEAT设计中，采用IRT理论对考试数据进行等值处理，第一个问题是模型的选取。研究采用的是目前普遍应用于多级记分测验的等级反应模型（Grade Response Model，GRM）中的同质模型，即每个项目只有一个区分度、每个等级上的区分度都是相同的。

设θ为被试潜在的特质，ui为一随机变量，作为对项目i的分级题目反应的记号，以ui（ui=0,1,2,…，mj）记录实际反应。记能力为θ的被试在第i题上得到ui分的概率为Pui(θ)，Pui'(θ)表示该被试在第i题目上的得分大于或等于ui的概率，则有

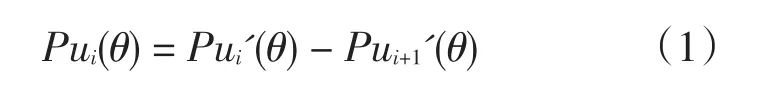
经分析，式1可以通过将多等级评分题目作“0，1”划分将Pui'(θ)转换成二级记分题目中的题目特征函数。在题目i中，令所有得分在ui或ui之上的被试为“通过”或“得1分”，得分小于ui的被试为“不通过”或“得0分”，则有Pui'(θ)=1，Pui+1'(θ)=0，等级反应模型的表达式为

其中，D为常数，ai为题目i的区分度，bui是题目i第ui等级的难度值，且第i题的等级难度是递增的，即b0＜b1＜…＜bmi。

等值处理的第二步是完成两个试卷版本的IRT量表转换。进行IRT量表转换的方法主要有3种：

1）固定共同题参数法（Fixed common item parameters）：先估计标杆卷上共同题的参数，在进行目标卷的参数估计时把这些共同题参数固定为已经得到的值，这样就使得目标卷的参数自动与标杆卷位于一个量表中。该方法可分为固定共同题单参数、双参数和三参数方法。

2）链接独立校准法（Linking separate calibration）：首先分别估计标杆卷和目标卷的题目参数，然后再依据一定的数学方法求解等值系数，将目标卷的参数转换到标杆卷上。

在NEAT设计中，由于不同考生群体分布可能不尽相同，经过参数估计，同一个锚题可以得到两个不同的能力分数θx和θy，还可以得到两组不同的题目参数ax、bx、cx和ay、by、cy，这两组参数估计值满足如下关系：

等值转换系数可采用矩估计法或特征曲线法求取。

（1）矩估计法（Moment method）：该方法使用题目参数的矩统计量来估计等值系数，主要方法包括平均数/平均数法、平均数/标准差法等。

平均数标准差法（Mean/Sigma，MS）。Marco在1977年提出该方法，MS法使用锚题的b参数标准差及其均数来获得转换系数A和B，其公式如下：

σbxv是从X测验估计出的锚题b参数的标准差，σbyv是从Y测验估计出的锚题b参数的标准差。

平均数平均数法（Mean/Mean，MM）。该方法是Lord和Hoover于1980年提出的，其做法是使用锚题的a参数的均值和b参数的均值来获得转换系数A和B，其公式如下：

特征曲线法（Characteristic curve method）：该方法是基于题目特征曲线的转换方法，其实质是通过减少题目特征曲线的差异实现量表转换。对于量表J和量表I，具有特定能力考生i和考生 j回答不同量表中试题的答对概率是相同的，其数学含义如下：

此式对于任何一个考生和任何一个题目理论上都是成立的。但是用测验样本的题目参数估计值代入，则会存在误差。求其误差平方有两种方法，由此引出两种基于题目特征曲线等值数据处理方法。

Haebara法。1980年黑巴诺（Haebara）首先提出用题目特征曲线法完成量表的转换，此方法是将一定能力的考生对每个题目的反应的题目特征曲线间的平方差进行累加，充分利用了更多参数信息，其数学表达式如下：

该函数式是锚题 j:V的总和。等式是将两个测验中每个题目特征曲线间的差的平方进行相加。Hdiff是在考生的基础上进行加和，其估计方式如下：

Stocking-Lord法。该方法是Stocking和Lord于1983年提出。Stocking-Lord方法与Haebara方法稍微不同，它是在固定考生的基础上，对题目i进行累加，由上式可推知：

上式的含义是同一考生在同一批题目上的真分数是相等的，并不受题目参数估计依据哪个群体的影响。代入具体的参数估计值，则两真分数之间存在误差，平方可得：

该函数式是锚题 j:V的特征曲线之和的差的平方。SLdiff是在题目基础上进行加和，其估计方法如下：

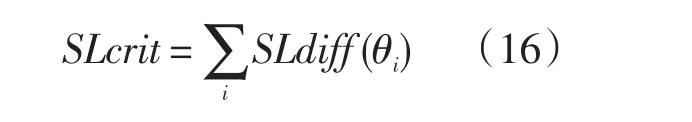
SLdiff(θi)表达式为给定能力值考生在锚题上的测验特征曲线在不同量表间差异的平方。相反，Hdiff(θi)表达式为对某一给定能力的考生在所有锚题上的题目特征曲线差异的平方和。无论是Hcrit还是SLcrit，均是在它们最小的条件下计算出A和B。将它们分别对A和B求偏导，并分别令其为0，可获得二元非线性方程组。一般采用牛顿迭代法估计出A和B。通常A和B初值采用均数标准差所估计的值为好（漆书青，2002：217）。

3）同时校准法（Concurrent calibration，CC）：与链接独立校准法不同，同时校准是将两个测验的数据合并，看成同一个测验，将一组被试未作答的另一个测验中非共同题上的反应当作缺失值，从而一次完成参数估计，得到的不同测验的题目参数自然就在同一个量尺之上。

2.2 等值效果的比较

等值过程会存在误差，等值效果的优劣依赖于不同等值方法引入等值误差的大小。为了评价等值的精确性，一般都采用比较等值误差大小的方法。一种等值设计或者方法产生的误差越小，这种等值设计或等值方法的效果就越好。

为评价等值效果，研究选择稳定性标准，主要通过计算评价样本敏感度的根均平方差（Root Mean Squared Difference，RMSD）和期望的差异平方根（REMSD）进行跨样本的一致性检验。跨样本一致性从另一个角度来说是等值的一个性质，理论上等值结果不受样本的影响。但实际上等值或多或少都存在样本的依赖性（Holland&Rubin，1982）。如果一种等值方法在不同的子样本中表现一致，虽然我们不能做出该方法是最好方法的结论，但是如果跨样本不一致，即这种方法对样本敏感，则该方法一定不是好的等值方法。

跨样本检验的具体做法是：把总体划分为有限的排他的几个样本，然后用总体和样本分别进行等值，进而比较样本等值结果与总体等值结果的差异。差异最小的方法即在不同样本中表现最为一致的方法就是较好的方法。下图以从考生群体O等值到考生群体Q为例说明跨样本检验框架。

图1 跨样本检验示意图

在NEAT设计中涉及两个被试群体，将被试群体P和Q各划分为不同的样本：{Pj}和{Qj}。WPj是指样本Pj的相应权重，WQj表示Qj在Q中的相应权重。WPj和WQj可被设定为某个值，只要总和为1。T是由被试组P和被试组Q按照一定比例组成的综合组。由此可知：

对于P和Q的样本{Pj}和{Qj}，也有相应的样本综合组Tj，可以定义为：

RMSD公式中的权重表示为：

用eTj(x)表示Tj中将X卷分数等值到Y卷上的分数，eT(x)表示综合组T上X卷分数等值到Y卷上的分数。eTj

(x)和eT(x)的等值方法相同。von Davier，Holland&Thayer（2003）把NEAT设计中的RMSD(x)定义为：

由于Y卷分数在综合组T中并不能直接观测到，因此综合组T中Y卷分数的标准差σYT的计算依赖于所选的等值方法。由公式可知，X卷上的每一个分数点对应到Y卷上都能计算出一个RMSD值，有的RMSD值比较小，有的则比较大，这样我们就无法直接客观地得出跨样本是否一致的结论。为了得到单一值，可计算REMSD指标，即期望的差异平方根。

上式中，ET{}是指T组在X卷上分部的平均数。

在计算统计量时，需要考虑的问题是统计量达到多大就可认为是显著的，即RMSD值和REMSD值都需要一个标准来衡量。Dorans，Holland，Thayer&Tateneni（2003）建议用DTM（Difference that mat-ters）这个指标。ETS多年来也是采用了这个标准。DTM是指报告分数的半个单位，即我们采用四舍五入时可以忽略的分数的一半。比如在某测验分数中，以1为分数单位，此时DTM=0.5。由于RMSD和REMSD这两个统计量通过σYT实现标准化，DTM也常常用它来实现标准化，标准化后的DTM常常用SDTM表示。如果RMSD值和REMSD值均小于SDTM，则说明等值的跨样本具有一致性。而且RMSD值和REMSD值值越小，则说明等值结果越精确、跨样本一致性越高；RMSD指标的变化趋势越平稳，则说明等值结果越稳定、跨样本一致性越高。

2.3 研究工具

使用业内公认的处理含有多级记分题目的考试的标准软PARSCALE软件进行参数估计，其他程序均使用Visual Foxpro 6.0自行编写。

3 研究结果

3.1 三份试卷各分测验原始分的CTT结果

由表1可以看出：新卷的原始平均分都远低于标杆卷；3个考生群体的分布（标准差）基本稳定；3份试卷各部分都略微偏难，新卷均比标杆卷稍难；3份试卷都具有较好的题目区分度；全卷的Alpha信度也是比较好的，分测验时Alpha信度略有降低，可能与题量的减少有关。

3.2 共同题信息

表2 标杆卷与新卷1共同题与分测验的相关

表3 标杆卷与新卷2共同题与分测验的相关

由于等值设计中，新卷1和标杆卷与新卷2和标杆卷进行连接的题型不同，故新卷1、新卷2包含的来自标杆卷共同题各不相同，但共同题题目数均在各分测验部分题目总数的一半左右。上表中列出了两份试卷共同题的相关分析结果。结果显示：该考试中共同题与所在分测验得分之间的相关较高，相关系数的P值均小于0.01。

3.3 跨样本一致性检验结果

研究以跨样本一致性检验结果作为评价等值方法的标准，所以首先对拆分的子样进行了代表性检验。样本代表性检验步骤如下：将参加新卷1的考生群体O（896人）、参加新卷2的考生群体P（906人）和参加标杆卷的考生为群体Q（1 420人）各随机分为两个独立的人数相等的样本（即O1和O2、P1和P2、Q1和Q2），然后通过独立样本T检验来检验六个样本的代表性。经检验，各样本均是各总体的无差样本，都能很好地代表该总体。

表1 各试卷分测验描述统计

跨样本一致性检验分别从六种方法的RMSD值和REMSD值的大小，以及RMSD指标的变化趋势来比较他们对样本的敏感性。

（1）RMSD值

图2 新卷1分测验一同时校准法RMSD值

将每种方法各个分数点的RMSD值与SDTM标准的情况作图如上（限于篇幅，文中仅列一图）。结果显示，每种方法对各个部分的等值的过程中，每个分数点跨样本的RMSD值，除低分段的个别分数点外，都基本低于SDTM的标准，即在RMSD指标上，四种方法都通过了SDTM标准的衡量，由此可见，四种方法都是可以实现跨样本等值的。

（2）REMSD值

从以上REMSD值表可以看出：新卷1和新卷2两个分测验四个部分的REMSD值都远低于SDTM的标准，在REMSD指标上，六种方法也通过了SDTM标准的衡量，由此可知，六种方法都实现了跨样本一致。另外，比较六种方法REMSD值的大小，分测验一时，两份试卷均是平均数平均数法的REMSD值最小，Stocking-Lord法次之；分测验二时，两份试卷均是固定共同题参数法的REMSD值最小，同时校准法次之。

（3）六种方法的RMSD指标比较

图3 新卷1分测验一四种方法RMSD值比较

表4 新卷1分测验一六种方法的REMSD值

表5 新卷2分测验一六种方法的REMSD值

表6 新卷1分测验二六种方法的REMSD值

表7 新卷2分测验二六种方法的REMSD值

图4 新卷2分测验一四种方法RMSD值比较

图5 新卷1分测验二四种方法RMSD值比较

图6 新卷2分测验二四种方法RMSD值比较

从六种方法各分数点RMSD值的大小和变化趋势来看，分测验一时，两份试卷大多数分数点均是平均数平均数法的RMSD值最小，同时也是起伏变化最小、最稳定的，Stocking-Lord法次之；分测验二时，两份试卷大多数分数点均是固定共同题参数法的RMSD值最小，同时也是起伏变化最小、最稳定的，同时校准法次之。

4 结论和进一步工作

从六种方法的跨样本一致性检验结果可以看出，六种方法在每个分数点的RMSD值和平均的REMSD值都基本低于SDTM的标准，都是可以作为该考试等值备选方法的。通过具体比较六种方法对样本的敏感性，从六种方法在每个分数点的RMSD值和平均的REMSD值的大小、以及RMSD指标的变化趋势的情况来进行优选，无论是精确性还是稳定性，分测验一均以平均数平均数法的等值效果最好，分测验二则以固定共同题参数法为佳。需要注意的是，该考试较高的试卷质量是各种等值方法效果较好的保证，现有的试卷结构是得到这一结论的前提。

研究对几种等值方法的探讨和比较都是基于同一个模型——等级记分模型之下进行的，未能涉及其他已有的多级记分模型，基于不同模型之下等值方法的比较仍是一个有待研究的内容。另外，等值效果的评价标准问题一直是等值研究中的难点，研究采用跨样本一致性指标这样的稳定性标准来进行检验。常用的几种评价标准——循环等值、模拟等值、大样本标准和研究采用的稳定性标准都各有其局限性，相比较起来稳定性的标准虽然不失为一种比较有说服力、可操作的标准，但其不能排除等值方法自身存在的“稳定的误差”的局限性，使比较的结果具有一定的不确定性，寻找一种更理想的方法作为评价标准是值得进一步研究的课题。

[1] 漆书青，戴海崎，丁树良.现代教育与心理测量学原理[M].北京：高等教育出版社.2002.

[2] 韩宁.应用项目反应理论等值含有多种题型考试的一个实例[J].中国考试，2008（7）：3-8.

[3] 谢小庆.对15种测验等值方法的比较研究[J].心理学报，2000：32-2.

[4] 周骏，欧东明，徐淑媛，戴海琦，漆书青.等级反应模型下题目特征曲线等值法在大型考试中的应用[J].心理学报，2005（6）：832-838.

[5] Brennan,R.L,(Ed.).Educational measurement(4th ed),Westport:American Council on Education and Praeger Publishers.2006.

[6] Dorans,N.J.,&Holland,P.W.Population invariance and the equatability of tests:Basic theory and the linear case.Journal of Educational Measurement,2000.37(4):281–306.

[7] Dorans,N.J.,Holland,P.W.,Thayer,D.T.,&Tateneni,K.Invariance of scoring across gender groups for three Advanced Placement Program examinations.In N.J.Dorans,(Ed.),Population invariance of score linking:Theory and applications to advanced placement program examinations.ETS RR-03-27.2003:79-118.

[8] Haebara,T.Equating logistic ability scales by a weighted least squares.Japanese Psychological Research,1980.22:144-149.

[9] Holland,P.W.,&Rubin,D.B.(Ed.).Test equating,New York:Academic Press.1982.

[10] Loyd,B.H.,&Hoover,H.D.Vertical equating using the Rasch model.Journal of Educational Measurement,1980.17:179-193.

[11] Marco,G.L.Item characteristic curve solutions to three intractable testing problems.Journal of Educational Measurement,1977.14:139-160.

[12] Samejima,F.Estimation of a latent ability using a response pattern of graded scores.Psychometrika Monograph Supplement,1969：17.

[13] Stocking,M.L.,&Lord,F.M.Developing a common metric in item response theory.Applied Psychological Measurement,1983.7(2):201-210.

[14] von Davier,A.A.,Holland,P.W.,&Thayer,D.T.Population invariance and chain versus post-stratification methods for equating and test linking.In N.Dorans(Ed.),Population invariance of score linking:Theory and applications to advanced placement program examinations.ETS RR-03-27.2003:19-36.

[15] Wingersky,M.S.,&Lord,F.M.An investigation of methods for reducing sampling error in certain IRT procedures.Applied Psychological Measurement,1984.8(3):347-364.