非参数项目反应理论回顾与展望

陈 婧 康春花 钟晓玲

1 引言

20世纪60年代，测验理论经历了从经典测验理论（Classical Test Theory，CTT）到项目反应理论（Item Response Theory，IRT）的巨大变革，IRT克服了CTT的种种局限，实现了对被试能力与其在特定项目上正确反应概率之间关系的模型化，这使得20世纪60～70年代以来，IRT成为心理计量学研究的核心内容。然而，IRT的应用与许多心理或教育测验的实际并不相符的，并在实际应用中给研究人员造成了困难。首先，IRT的基本假设难以满足。IRT理论基于能力的单维性、局部独立性和单调性这三条强假设。当所选择的参数模型支持这些假设时，所拟合的模型能够提供大量关于项目和被试的信息。而在实际应用中，所收集的数据往往难以满足IRT的基本假设。其次，IRT要求在大样本的基础上才会有较好的精确性。但是，在实践中，收集的数据往往达不到IRT对大样本的要求，则IRT参数估计的精确性必然受到影响。正因为如此，IRT的理论研究一般以模拟研究居多，而应用研究则在大尺度测评中才显现优势，在日常教学及学校或课堂的小样本测试中则无用武之地。因此，当实际测评中的数据并不能完全吻合IRT的强假设以及样本容量较小时，非参数项目理论反应理论（Non-parametric Item Response Theory，NIRT）为突破此困境提供了原理和方法。这是因为相比IRT，NIRT除了提供了与实际日常情景更适应更有弹性的理论框架，还发展出适宜小样本数据的更简便易行的分析方法（Junker&Sijtsma，2001）。因此，在项目反应理论蓬勃发展的同时，更适于日常教学及其测评情境的非参数项目反应理论应该得到更多的关注及实践应用。

2 非参数项目反应理论的数学模型

非参数项目理论的提出更加完善了参数项目反应理论。在实际的测量中并不是所有的题目都能够拟合项目项目反应理论中的各个参数，但是这些题目却在测量中同样起十分重要的作用，非参数项目反应理论就很好地解决了这一问题（Sijtsma，1998）。非参数项目反应理论假设被试的能力水平与答对题目的概率相关，能力水平越高的被试其答对的概率就越高，这点与参数项目反应理论的假设是相同的。与参数项目反应理论不同的是被试不以特质值θ和题目的参数a、b描述被试的特质水平，而是直接从被试在测试中所得的分数进行排序得出被试特质水平的高低（雷新勇，2006）。根据理论假设的不同，可以将非参数项目反应理论分为单调均质模型（Monotone Homogeneity Model,MHM）和双单调模型（Double Monotonicity Model,DMM）。

2.1 单调均质模型

Mokken在1971年提出单调均质模型（MHM），以单维性、局部独立和项目反应函数单调性假设为基础（Sijtsma,1998）。单维性假设所有题目测量的是相同的潜在特质。局部独立性是假设被试本身应答的独立性和被试之间应答的局部独立性，所有的变化都是由被试的潜在特质引起的，题目与被试之间也是独立的。项目反应理论的单调性假设说明被试答对的概率是与其能力有关的，被试能力高答对的概率就高，根据被试在试题的得分对被试的潜在特质进行排序。

设θ是一个固定的X+值，s和t是两个不同的X+值，令0＜s＜t＜k，则有

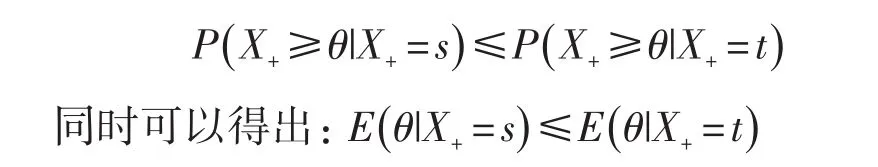
说明被试的测试得分与其能力值成正相关，测试总分为s的被试其能力值低于测试总分为t的被试。

2.2 双单调模型

双单调模型也是Mokken在1971年在单调均质模型的理论假设上提出的。DMM比MHM具有更严格的理论假设，它在MHM的基础上再加上项目反应函数非相交性为基础的非参数项目反应理论模型，即对潜在特质为θ的所有取值，k道项目反应函数不相交，也可以说单调均质模型是双单调模型的一个特例。对于所有的试题，其期望的条件试题得分等于项目反应函数值：

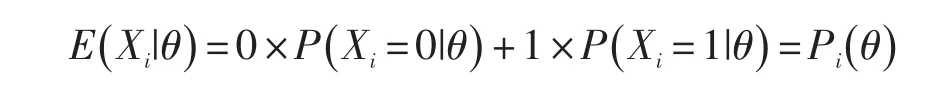
对于所有的θ取值有：

在θ的所有取值范围内，按照试题的平均分进行排序，排序结果不变。通过P值对题目排序，则可以得到题目顺序为：P1≤P2≤…≤Pk。

3 非参数项目反应理论研究

3.1 非参数项目反应理论的理论研究

3.1.1 非参数与参数估计方法的比较

对非参数项目反应理论的理论研究主要集中在对非参数估计方法和参数估计方法的比较研究上，大部分对非参数估计方法的研究都是基于核平滑（kernel smoothing）方法而展开。如Ferrando（2004）在未限制曲线单调性的前提下，采用RISE作为拟合优度指标，比较了kernel方法与线性的连续反应模型对于连续的人格量表项目的特征曲线的估计。研究发现kernel方法能够提供与参数模型相当的拟合精度。同时，Lei，Dunbar和Kolen（2004）在释放曲线单调性假设的前提下，基于WtRMS、Wt-MABS指标，比较了kernel方法与参数方法对于多项选择题的项目特征曲线估计的差异。该研究还探讨了非参数方法中小样本对于参数方法与非参数方法的影响。研究发现，非参数方法在小样本的条件下仍显示出较好的拟合优度，kernel方法对于干扰选项的特征曲线的估计能够提供项目编制质量的有效信息。

3.1.2 非参数估计方法之间的比较

近几年来，国内外对非参数项目理论的研究，除了对非参数估计方法与参数估计方法的比较研究之外，也有研究者在考察非参数估计方法和参数估计方法之间的差异的同时，还考察了不同的非参数估计方法之间的差异。如Lee（2007）使用RMSD作为拟合优度指标，比较了保序回归、平滑的保序回归和kernel方法与参数方法对于二分项目的项目特征曲线的估计。该研究在限制曲线单调性的前提下进行，并探讨了违背单调性的题目数量这一因素对曲线拟合度的影响。研究发现，平滑保序回归在使用相应的内核函数时能够提供更准确的估计并满足严格的单调性条件。而当项目数量以及样本大小增加时，在各种条件下的平滑保序回归和kernel方法对项目特征曲线（Item Characteristic Curve，ICC）的估计会产生相似的结果。而当违背单调性的题目数目增加时，参数方法估计的拟合优度会受到较为严重的影响。

此外，也有研究者使用不同非参数估计的方法评估了参数项目反应理论拟合优度的差异。如Manuel J.Sueiro&Francisco J.Abad（2011）认为，非参数项目特征曲线和参数项目特征曲线之间的距离可以以根的综合误差指数为指标，并能够将之作为项目反应理论拟合优度的一种索引。所以他们将潜在特质的后验分布作为非参数模型，与另一个基于核平滑（kernel-smoothing，KS）方法的模型之间进行了性能的比较。对错误率和效率的评估使用了 2PLM（two-parameter logistic model）和三种类型的实际不拟合项目。研究发现，对于拟合的项目，参数和非参数项目特征曲线之间的距离在两种方法上都会随着样本的增大而下降。KS的综合误差平方根会随着测验长度的增加而下降。而在效率方面，后验分布的方法在小样本方面更有优势，而短测验也同样在此方面表现出了优势。另外，Alexandra A.H.等（2004）对不同的非参数维度评估程序进行了比较研究。研究者使用2×2×6×4×3×4的研究设计模拟数据以比较MSP、DETECT、HCA/CCPROX以及DIMTEST这四个软件在默认设置下对维度评估的异同点。结果发现，使用潜在特质的协方差矩阵数据位基础的分析软件（DETECT&HCA/CCPROX）在拟合模型方面优于使用标准无条件方差矩阵数据的软件（MSP）。同时，研究者还对DETECT和DIMTEST进行了接受或拒绝能力的单维性假设的正确性研究。研究发现，这两个软件并不能一直正确反映题库的真实维度。

3.1.3 非参数模型与数据的拟合验证

除了参数估计方法上的比较研究，还有一些学者对非参数项目反应理论其他方面进行了一些研究。如 George Karabatsos&Ching-Fan Sheu（2004）研究了NIRT的单调均质模型和双单调模型在顺序限制的贝叶斯推理体系中（order-constrained Bayes inference framework）分析二级反应向量的实用性。研究使用NAEP测试的实践数据分析了用以估计顺序限制参数的Gibbs抽样的实施，并用后验分布来对NIRT的项目单调性、项目排序的不变性以及局部独立性假设进行了验证。结果表明，无论是NIRT的单调均质模型还是双单调模型都能够实现和NAEP测试的实践数据较好的拟合。Wilco H.M.Emons（2008）对多级计分的项目反应得分进行了非参数个人拟合分析的研究。研究者认为，个人拟合方法通常被用来揭露非典型性的测验表现，以此来反应一个测验中个别项目的分数的样本。而和参数个人拟合统计不同，非参数个人拟合统计并不需要一个参数模型。研究者在研究中调查了非参数个人拟合统计对多级计分项目数据概括的有效性，并使用了模拟研究研究了不同的测试和项目参数，研究发现在检测严重的不拟合时，对古德曼错误（Guttman errors）的计数是有效的。这个模拟研究更进一步发现，在大多数情况下，非参数个人拟合统计在检测异常的项目分数向量时和常用的参数个人拟合统计是同样有效的。

3.2 非参数项目反应理论的应用研究

3.2.1 量表制定

目前对NIRT的应用研究相对理论研究而言比较少，大部分的研究主要集中在对量表的制定上。如Klaas Sijtsma等(2008)使用非参数估计方法分析了生活质量量表并将之在在世界卫生组织的研究中进行了应用。研究者调查了非参数同质单调模型衡量和构建生活质量量表的有效性，此生活质量量表是由多岐项目组成，并将非参数同质单调模型和常用的参数等级反应模型进行了比较。结果发现，非参数单调同质模型高度适合对与健康相关的生活质量情况的数据分析，而参数等级反应模型也为模型拟合添加了有趣的特性。研究者同时使用了单调同质化模型和等级反应模型对世界卫生组织生命质量量表数据进行了分析，并以单调同质模型为基准分析取得了每个内容域的一维尺度。可扩展性系数进一步表明，一些项目在其他同等尺度的其他项目上具有有限的可扩展性。而参数估计方法可能会导致一些项目被否决。

国内也有研究者展开了对非参数项目反应理论在制定量表方面的应用研究，如王鹏（2005）研究了NIRT在公共管理中的应用，将其与经典测验理论（Classical Test Theory，CTT）和IRT在公共管理量表制定的实例中进行了比较研究，该研究发现，CTT对样本的依赖性很高；IRT几乎不受被试变化的影响，但是会受到样本数量的影响；而NIRT在小样本中保持了较高的测验精度，且测验结果也比较稳定。张军（2010）使用了非参数项目反应理论的Mokken量表及其构建程序MSP，探索性地分析HSK[初中等]听力、语法结构和阅读三个部分中40个题的潜在维度，并籍此评价此方法的优劣。研究表明：题组是多维的，阅读题的区分能力和一致性最强，能有效地聚合成一类；听力题次之，语法结构题最差；同时，他还发现，使用NIRT进行维度分析存在很多不足，尤其是题目区分能力对分类的干扰与界定分类阶段的标准存在较大的问题。

3.2.2 个性数据及项目功能差异分析

除了在量表制定方面的研究，也有研究者应用非参数项目反应理论展开了其他方面的研究。如Rob R.Meijer&Joost J.Baneke（2004）对NIRT在个性和精神病理学尺度的建立和心理测量分析的适用性方面进行了研究，并和三个参数IRT模型进行了比较研究。他们以MMPI中的抑郁量表为研究对象，发现在分析个性数据时，非参数IRT模型要优于参数IRT模型，并且非参数IRT模型更便于应用，同时可以避免参数IRT模型在分析数据时的失误。

雷新勇（2006）研究了NIRT在教育考试中的应用，用单调均质模型从16道听力试题中选出11道题组成了单维量表，再利用双单调模型对单维量表进行功能偏差研究发现，有5道试题在女生子群体中的排序与在男生子群体以及整个群体排序不同,显示女生子群体作出正确应答的概率明显高于男生子群体作出正确应答的概率。这种差异至少部分是由两个子群体听力能力上的差异引起的。

4 非参数项目反应理论的新发展：非参数认知诊断理论

4.1 非参数认知诊断理论的兴起

在近二三十年来发展的新一代测量理论中，把个体任务完成所需要的知识、认知加工技能等称为认知属性（Cognitive Attribute），把对个体任务完成中认知过程、加工技能或知识结构中优势与不足的诊断称为认知诊断评估（Cognitive Diagnosis Assessment,CDA），其中用于对学生知识结构进行诊断评估的心理测量模型称为认知诊断模型（Cognitive Diagnosis Model,CDM）。Fu和Li总结出60多种常见的诊断模型，其中，应用较为广泛的核心模型有逻辑斯蒂潜在特质模型（LLTM，（Fischer,1973））、规则空间模型（RSM，（Tatsuoka,1983））、属性层级模型（AHM,（Leighton,Gierl,&Hunka,2004））、DINA模型（（Junker&Sijtsma,2001））、融合模型（FM，（Hartz,2002））、DINO 模型（（Templin&Henson,2006））等（Fu&Li,2007）。

以上认知诊断模型都属于参数模型，目前对这些参数认知诊断模型的参数估计主要包括边际最大似然估计以及贝叶斯估计，而这种以参数项目反应理论为基础发展起来参数估计方法在进行认知诊断模型的参数估计时，尚且存在较多的不足。首先，当所测的认知属性较多，样本量较大的时候，参数估计的时间很长，给研究者带来很多不便（已有研究表明，当属性个数在8个时，EM算法和MCMC估计都需要耗费很长的时间）；其次，当进行短测验或小样本施测时，样本容量达不到进行参数数据分析的要求，又会造成较大的估计误差，致使所估计的参数精确性很低。而在实际教学和测评中，所涉及的认知属性往往是较多且关系复杂，而参加测评的对象也不是成千上万的（比如某校学科组或任课老师想要了解四年级学生在数学应用题或图形与几何问题解决中的情况），此时，相对于参数认知诊断模型，非参数认知诊断模型可能更加适宜。在此背景下，非参数认知诊断模型应运而生。

4.2 非参数认知诊断模型

Henson、Templin&Douglas在2007年提出，在DINA模型数据下，对于一个给定的Q矩阵，其观察总分为他们认为，在联合模型下，Wik能够提供被试的能力信息。

Chiu在2008年的研究发现，可以使用K-MEANS算法以及等级聚类法对总分进行聚类。

Chiu的这个研究被认为是关于非参数认知诊断的第一个原理性的成果，他表示，在恰当的技术条件下，只要每一个属性都存在非零比例的单一项目，那么当项目j增加时，可以涵盖所有的掌握模式。

Ayers、Nugent&Dean(2008)使用正态分布的数据进行了研究，

从经验上来讲，相对于对总分向量的聚类分析法，使用能力向量的聚类分析法所估计的能力参数更接近拟合的DINA模型，尤其在数据缺失的情况下。

4.3 非参数认知诊断研究

Brian在2011年展开了对非参数项目反应理论的认知诊断研究。他认为之所以要展开非参数认知诊断的研究，一方面是因为非参数项目反应理论在心理学研究中是可以应用的，并且还在被不断地研究。通过非参数项目反应理论，研究者可以考虑以最低限度的假设来了解项目反应理论模型的基本结构以及一般的能力变量的测量模型。另一方面，在研究认知诊断模型时，就像参数项目反应理论一样，研究者都会需要通过估计项目参数来评估项目的质量以及通过能力值来估计被试掌握或者未掌握某种认知属性。

Brain（2011）在文章中介绍了两种非参数的方法来处理认知诊断模型的数据。一种方法是提供联合结构的假设以及正确的Q矩阵，用聚类分析将有相同模式的认知属性或技能的被试分成不同的组别来处理作答数据(Ayers et al.,2008;Chiu,2008;Nugent et al.,2009)。另一种方法是将被观测到的项目之间的联合结构作为发现推测的第一步或者将项目之间的关系作为等价的前提条件，然后将之作为构成Q矩阵结构的可能成分来分析(Desmarais&Pu,2005;Tucker,2009)。这两种方法都还处于其研究的初期阶段，但是它们都指向了非参数方法可能存在的重要优势。当面临庞大的数据库时，它们开发了简单而便于应用的数据处理算法，而且它们还开始促成一些具有操作性特征的认知诊断模型的产生。

综上所述，我们可以看到，虽然对非参数认知诊断研究已经展开，一些特殊的非参数方法也开始初具规模，但总体而言，研究还是相对较少，目前为止，还没有开展关于非参数认知诊断的应用研究。这些都有待于后续的研究者进一步研究。

5 总结与展望

5.1 非参数项目反应理论研究优势

非参数项目反应理论作为一种在参数项目反应理论的基础上发展起来的测量理论，它为参数项目反应模型适应的局限性提出了更适应更有弹性的框架，因非参数项目反应模型对数据的要求更宽松而比参数项目反应模型应用的范围更广。同时，非参数项目反应理论不像参数项目反应理论那样通过对项目参数的估计，以期获得更为精确的测量结果，而是通过对样本数据的估计来获得一个从高到低或从低到高的排序，不仅简化了复杂而繁琐的参数估计的运算过程，而且也为广大的测量人员提供了方便，比较简便容易操作，实用性更强。而在以非参数项目反应理论基础上发展起来的非参数认知诊断，成为对参数认知诊断的重大补充。因为它更为宽松的适用环境，使其在实际应用中，更吻合实际，应用性更高，从而能更好地吻合新课程背景下老师想要了解学生问题解决过程的需要。

5.2 非参数项目反应理论的研究展望

回顾几十年来研究者对非参数项目反应理论的研究，我们可以发现，虽然非参数项目反应理论自产生以来，一直有研究者对其进行研究。但总体而言，目前的非参数项目反应理论的研究研究队伍依然小而分散，后备力量相对不足。NIRT研究自兴起至今，研究人员队伍一直处于一种相对分散的状态，研究力量也不是很集中，因此研究很难系统深入，对其理论的研究还不像参数项目反应理论那样涉及测验等值、题库建设、多级评分模型、计算机自适应考试、DIF等各个方面。

同时，我们还发现，尽管对NIRT的研究已经取得了一些成果，但是其理论研究领域偏窄，研究主要集中在对非参数项目反应理论尤其是对非参数估计方法与参数估计方法的比较研究上，且这些研究大多数都是模拟研究，对其应用研究展开的极少。从总体趋势上来看，对NIRT的理论研究仍处于初级阶段，相对于参数项目反应理论的蓬勃发展，非参数项目反应理论还有待于今后展开更多的研究。

此外，就目前的文献来看，尽管有一些研究者如Klaas Sijtsma、雷新勇等对非参数项目反应理论在应用方面展开了研究，但我们可以明显看到，NIRT应用研究简直是凤毛麟角，且更多的集中于认知、情感测验开发，比较少涉足技能领域，而在认知领域中也偏重于教育领域，较少心理认知加工模式上的应用，这使得NIRT的应用范围相当狭窄，许多NIRT的优良功能尚未充分开发。

综上所述，我们可以看到，非参数项目反应理论无论是在理论研究还是在应用研究方面都有比较好的发展前景，未来还需要更多的研究人员投入到对其的研究中，以期获得更大的发展。

[1] 雷新勇.非参数项目反应理论模型及其在教育考试中的应用[J].考试研究，2006(2)：53-71.

[2] 王鹏.NIRT在公共管理中的应用及与CTT和IRT在实例中的比较[D].东北大学硕士学位论文，2005.

[3] 张军.非参数项目反应理论在维度分析中的运用及评价[J].心理学探新，2010(30)：80-83.

[4] Ayers,E.,Nugent,R.,&Dean,N.Skill set pro fi le clustering based on student capability vectors computed from online tutoring data.In R.S.J.d.Baker,T.Barnes,&J.E.Beck(Eds.),Educational data mining 2008:1st International Conference on Educational Data Mining,Proceedings,2008：210-217.

[5] Brian,W.Junker.The Role of Nonparametric Analysis in Assessment Modeling:Then and Now,2011：67-82.

[6] Chiu,C.Cluster analysis for cognitive diagnosis:Theory and applications.Unpublished doctoral dissertation,Department of Educational Psychology,University of Illinois at Urbana Champaign,2008.

[7] De Jong.A.&Molenaar,I.W.An application of Mokken’S model for stochastic Cumulative scaling in psychiatric research.Journal of Psychiatric Research,1987,21.

[8] Edward E.Roskam,Arnold L.van den Wollenberg and Paul G.W.Jansen.The Mokken Scale:A Critical Discussion Applied Psychological Measurement,1986,10:265.

[9] Fischer,Gerhard H..The linear logistic test model as an instrument in educational research.Acta psychologica,1973,37(6):359-374.

[10] Fu,J.,&Li,Y.Cognitively diagnostic psychometric models:An integrative review.Paper presented at the The annual meeting of the National Council on.Measurement in Education,Chicago,IL,2007.

[11]George Karabatsos&Ching-Fan Sheu.Order-constrained Bayes inference for dichotomous models of unidimensional nonparametric IRT,2004.

[12] Hartz,S.M.A Bayesian framework for the unified model for assessing cognitive abilities:Blending theory with practicality.Unpublished doctoral dissertation,University of Illinois at Urbana-Champaign,Urbana-Champaign,IL,2002.

[13] John Sachs.Yin kum Law.Carol K K Chan.A nonpararnetric item analysis of a selected item subset of the Learning Process Questionnaire,2003,73.

[14] Junker.B.W.&Sijtsma.K.Nonparametric Item Response Theory in Action:An Overview of the Special Issue.Applied Psychological Measurement,2003,25(3):211-220.

[15] Junker,B.W.,&Sijtsma,K.Cognitive assessment models with few assumptions,and connections with nonparametric item response theory.Applied Psychological Measurement,2001,25(3):258-272.

[16] Kristin A Duncan&Steven N MacEachern.Nonparametric Bayesian modelling for item response,2008.

[17] Klass Sijtsma.Ivo W Molenaar Introduction to Nonparametric Item Response TheoryM.London：International Educational and Professional Publisher,2003,60.

[18] Klaas Sijtsma,Wilco H.M.Emons,Samantha Bouwmeester,Ivan Nyklíček,and Leo D.Roorda.Nonparametric IRT analysis of Quality-of-Life Scales and its application to the World Health Organization Quality-of-Life Scale(WHOQOL-Bref),2008.

[19] Klaas Sijtsma.Methodology Review:Nonparametric IRT Approaches to the Analysis of Dichotomous Item Scores Applied Psychological Measurement,1998,22(3).

[20] Leighton,J.P.,Gierl,M.J.,&Hunka,S.M..The Attribute Hierarchy Method for Cognitive Assessment:A Variation on Tatsuoka's Rule-Space Approach.Journal of Educational Measurement,2004,41(3):205-237.

[21] Manuel J.Sueiro,Francisco J.Assessing Goodness of Fit in Item Response Theory With Nonparametric Models:A Comparison of Posterior Probabilities and Kernel-Smoothing Approaches,2001.

[22] Molenaar,I.W.&Sijtsm,K.Users manual MSP5 for Windows[M].Crroningen：lee-ProGA～IMA,2000,23.

[23] Nichols,P.D.,Chipman,S.F.&Brennan,R.L.Cognitively diagnostic assessment.Hilldale,NJ:Lawrence Erlbaum,1995.

[24] Pui-Walei,Stephen B.Dunbar and Michael.J.Kolen A Comparison of Parametric and Nonparametric Approaches to Item Analysis for Multiple-Choice Tests,2004.

[25] Ramsay.J.Kernel Smoothing approaches to nonparametric item characteristic Curve estimation,1997.

[26] Rob R.Meijer,Joost J.Baneke.Analyzing psychopathology items a case for nonparametric item response theory modeling，2004.

[27] Tatsuoka,K.K.Rule space:An approach for dealing with misconceptions based on item response theory.Journal of Educational Measurement,1983,20(4):345-354.

[28] Templin,J.L.,&Henson,R.A.Measurement of psychological disorders using cognitive diagnosis models.Psychological Methods,2006,11(3):287.

[29] Young-Sun Lee.A Comparison of Methods for Nonparametric Estimation of Item Characteristic Curves for Binary Items,2007.