交流伺服电机宽速度范围运行性能研究

吉智，何凤有

（1． 中国矿业大学 信息与电气工程学院，江苏 徐州221008；2.江苏省电力传动与自动控制工程技术研究中心，江苏 徐州221008）

1 引言

目前中小容量交流伺服电机中最常见的是永磁同步电机，其转子结构包括面装式、插入式和内装式[1]。其中面装式转子磁极易于实现优化设计，气隙磁链趋近于理想正弦，应用最为广泛[2]。 但随着高速加工技术的发展，对电机的性能提出了更高的要求，如何拓展运行范围，提高高速运行时的转矩输出能力，成为当前的研究热点之一。

文献[3]综合考虑电流、电压限制，通过电压外环对去磁电流和转矩电流进行控制，保证了电流跟踪特性。 文献[4]讨论了凸极率和去磁因数对输出功率的影响。 文献[5]提出了一种根据d轴电流误差控制去磁电流和转矩电流避免电流调节器饱和的方法。 在文献[6]中d 轴电流在恒转矩区由最大转矩电流比曲线查表获得，在弱磁区由电压环控制；q 轴电流由转矩指令、d 轴反馈电流和电压相角共同确定，实现了全速度范围最大转矩输出。 文献[7]对最大转矩磁链比控制进行了研究，推导了定子电流计算方法。

这些研究成果除文献[4]外，基本出发点在于设计合适的电流分配策略，以提高高速运行时的转矩输出能力。 其不足在于这些研究是从控制的角度出发，没有考虑电机本身参数对运行性能的影响。 文献[4]研究了凸极率和去磁因数对输出功率的影响，但没有涉及到其他参数。 本文针对伺服系统中常见的面装式永磁同步电机，通过仿真研究了永磁磁链、电枢电感、绕组电阻3 个参数对输出转矩、功率、功率因数、去磁因数的影响，并进行了实验验证。 以期能够根据对不同参数电机运行性能的研究确定最佳电机参数，提高系统性能。

2 电机模型与运行约束条件

利用固定于转子上的dq 同步旋转坐标系，并沿用理想电机的一系列假设[2]，可以得出如下电机数学模型。

定子电压方程

输出转矩

稳态下，式（1）中的第1项为零，同时高速运行时，忽略定子电阻压降，可得电压约束

电流约束

最大功率曲线为过D 点，且垂直于d 轴的直线[2]，当Ψf/Ld＜imax和Ψf/Ld＞imax时电流极限轨迹和电压极限轨迹分别如图1a、图1b 所示。

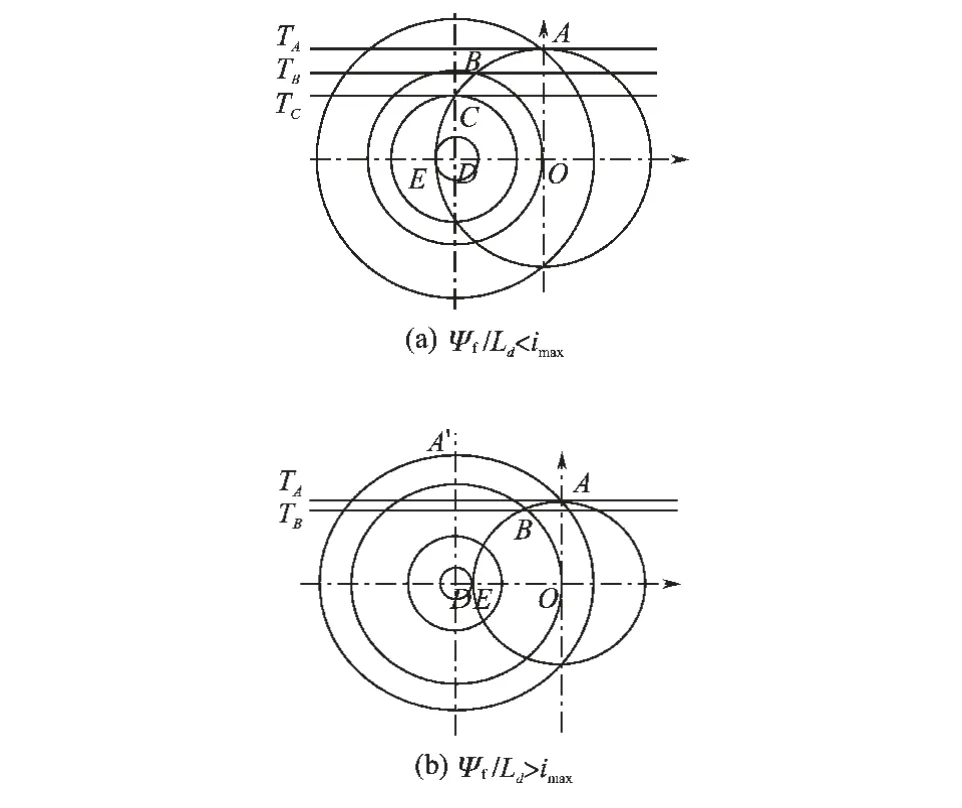
图1 全速度范围定子电压、电流轨迹Fig.1 Stator voltage and current tracks of full velocity range

定义电机的功率因数为

定义去磁因数为

式中：δ，φ′，φ，ω，Rs分别为功角、内功率因数角、功率因数角、感应磁场角速度、电枢绕组电阻；Ψf为转子永磁磁链；Ld，Lq分别为d 轴电感、q 轴电感；is，id，iq，imax分别为电枢电流、 电枢电流d 轴分量、 电枢电流q 轴分量、 电机最大电流；us，ud，uq，umax分别为电枢端电压、端电压d 轴分量、端电压q 轴分量、逆变器输出最大电压。

3 全速度范围电流控制策略

对于伺服电机，低速时希望输出转矩要尽可能大，而在高速时更重视有效转速，即输出要求转矩时的最高转速。 因而可以根据转速分段实现全速度范围最大转矩电流控制策略。

3.1 低速区域（ω＜ωA）

此时绕组中电流和旋转反电势较小，可以忽略。 对于给定转矩只要合理配置dq 轴电流分量，使定子电流合矢量is最小即可，称之为转矩电流比最大控制，对于面装式永磁同步电机，令id=0即可实现这种控制方法[2]。 电机启动时对应于图1中的A 点，以最大转矩加速运行，随着转速的升高电流减小，当达到所要求的转速时，输出转矩和负载平衡。 其电流控制规律是：

将式（7）代入式（3），可求出A 点对应的转速ωA，称为转折速度。

3.2 中速区域（ωA≤ω＜ωC）

随着转速升高，旋转反电势增大，当接近逆变器供电电压时，电流调节器饱和，限制了转速进一步提高。 从式（3）可见，由于永磁电机励磁无法调节，只能增大id或减小iq来保持电压平衡。在图1中使电流矢量沿电流极限圆从A 点至C点，由于随着转速增大，去磁电流id增大，合磁场减小，称之为一般弱磁控制。 将电流极限圆代入电压极限圆，可得其电流控制规律：

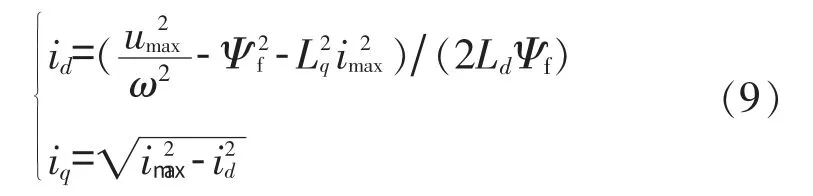
令id=-imax，iq=0代入式（9），可得一般弱磁控制理想最高转速ωE（在图1b 中对应E 点）为

3.3 高速区域（ωC＜ω）

当Ψf/Ld＜imax时最大功率曲线和电流曲线存在交点，在图1a 中控制电流矢量沿直线从C 点至D 点，称之为最大功率弱磁控制，电流控制规律为

图1a 中，在C 点一般弱磁控制向最大功率弱磁控制切换，令id=-Ψf/Ld代入式（9）中，可得：

图1中D 点对应的转速为最大功率弱磁控制所能达到的最高转速，理论上是无限大，当然由于机械结构等因素限制，实际上这个速度是达不到的。 当Ψf/Ld＞imax时如图1b 所示，最大功率弱磁控制不能实现。

4 仿真与实验

在电机研究中常采用转速电流双闭环系统模型[8-10]。 但这种模型很难区别实验结果的差异是由控制参数的变化引起的，还是由不同的电流控制方法造成的。 本文利用电机数学模型和不同电流控制规律构造仿真模型[11-12]，避免了控制器参数对结果的影响。

实验利用Matlab 的xPC-target 工具箱，由上位机、目标机、功率驱动板和电机构成，见图2。

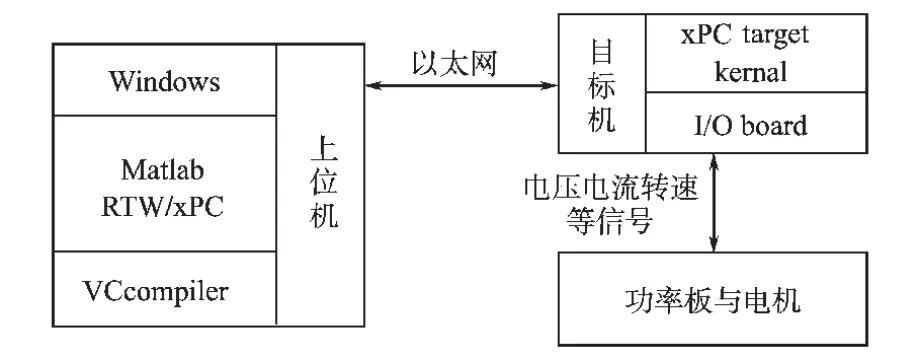
图2 实验系统构成Fig.2 Experimental system structure

在上位机中利用Matlab 设计电流控制算法和数据采集软件，编译后通过以太网下载到目标机中执行。 目标机通过数据采集卡输出6 路PWM 信号控制功率驱动板并采集电压、 电流与转速信号。 这种方案利用PC 构建快速原型控制系统，无需低级语言编程，为算法实现和数据采集、处理带来了方便。

表1列出了电机的实验参数，实验时每次仅选取一个参数作为变化参数（遍历取值点上的各值），其余非变化参数则取标准值。

表1 仿真电机参数Tab.1 Parameters for tested motor

4.1 永磁磁链对运行性能的影响

不同永磁磁链对电机运行性能的影响见图3。 Ψf=0.12，0.25，0.32（Wb）3 条曲线对应于Ψf/Ld＜imax；Ψf=0.37，0.4，0.6 （Wb）3 条曲线对应于Ψf/Ld＞imax。对于图3a 中Ψf=0.25（Wb）曲线，从零经A 点（用*标记）至0 点的实线为id=0 控制，A 点经C （用+标记）点至E 点的虚线为一般弱磁控制，C 至D 点的实线为最大功率弱磁控制。 因此全速度范围优化电流控制轨迹是由零点经A，C 至D 的曲线。

由图3a 可见，在转折速度（A 点）以下的恒转矩区转矩和转速无关，但却随着永磁磁链的增大而显著增大；超过转折速度后的弱磁区域，转矩随转速的增大而快速降低，当Ψf/Ld＜imax时，无论一般弱磁控制还是最大功率控制，永磁磁链增大，输出转矩均增大。 但速度越高的区域，转矩增大的程度越小；当Ψf/Ld＞imax时，输出转矩随永磁磁链变化的关系比较复杂，速度较低时随着永磁磁链的增大而增大，速度较高时则相反。

从图3b 可见，在恒转矩区域，随着永磁磁链的增大，输出功率增大；超过转折速度后，当Ψf/Ld＜imax时，无论一般弱磁控制还是最大功率弱磁控制，永磁磁链增大，输出功率均增大并最终保持在最大输出功率；当Ψf/Ld＞imax时，输出功率随永磁磁链变化的关系比较复杂，虽然最大功率为恒值和永磁磁链无关，但速度较低时随着永磁磁链的增大而增大，速度较高时则相反。 并且永磁磁链越大随转速增加输出功率衰减越快。

由图3c 可见，在恒转矩区域，随着永磁磁链的增大，功率因数增大；超过转折速度后，当Ψf/Ld＜imax时，无论一般弱磁控制还是最大功率弱磁控制，永磁磁链增大，功率因数均增大并随转速增大趋近单位功率因数。 同时转速较小时，功率因数增大较明显，转速较大时，功率因数增大幅度较小；当Ψf/Ld＞imax时，输出功率随永磁磁链变化的关系比较复杂，虽然最大功率因数近似于单位功率因数和永磁磁链无关，但速度较低时随着永磁磁链的增大而增大，速度较高时则相反，并且永磁磁链越大随转速增加功率因数衰减越快。

图3 永磁磁链对电机运行性能的影响Fig.3 Influence of permanent magnetic flux to motor run property

从图3d 可见，去磁因数和永磁磁链的关系，存在1 个分界点F，在此以下速度区域磁链增大，去磁因数增大；在此以上速度区域则相反。Ψf/Ld＞imax时只能采用一般弱磁控制，去磁因数小于1；Ψf/Ld＜imax时超过C 点后如还采用一般弱磁控制则去磁因数可能远大于1，而切换至最大功率弱磁控制则可将去磁因数限制在1。因此最大功率因数控制有利于保障永磁材料的安全工作。

增大永磁磁链对于改善电机中低速运行性能比较有利，但会降低电机转折速度和弱磁运行最高速度，不利于扩展电机的高速运行范围。 对于最大功率弱磁控制，增大永磁磁链对于提高其输出功率很有效。

4.2 电枢电感对运行性能的影响

电枢电感变化对电机运行性能的影响见图4。图4中，L=0.02，0.026，0.04，0.06（H）4 条曲线对应于Ψf/Ld＜imax；L=0.01，0.015（H）2 条曲线对应于Ψf/Ld＞imax。

由图4a 可见在恒转矩区域，输出转矩为恒值和电枢电感无关；超过转折速度后，当Ψf/Ld＜imax时，无论一般弱磁控制，还是最大功率控制，电枢电感增大，输出转矩均减小。 但速度越高的区域，转矩减小的程度越小；当Ψf/Ld＞imax时，输出转矩随电枢电感变化的关系比较复杂，速度较低时随着电枢电感的增大而减小，速度较高时则相反。

从图4b 可见，在恒转矩区域，随着电枢电感的增大，转折点A 对应的输出功率减小；超过转折速度后，当Ψf/Ld＜imax时，无论一般弱磁控制还是最大功率弱磁控制，电枢电感增大输出功率均减小；当Ψf/Ld＞imax时，输出功率随电枢电感变化的关系比较复杂，虽然最大功率为恒值和电枢电感无关，但速度较低时随着电枢电感的增大而减小，速度较高时则相反。 并且电感越小随转速增加功率衰减越快。

由图4c 可见，在恒转矩区域，功率因数随电感的增大而减小。 超过基本转速后的区域，当Ψf/Ld＜imax时，无论一般弱磁控制还是最大功率弱磁控制，电枢电感增大功率因数均降低，但随着转速增大而增大，最后均接近最大值1；当Ψf/Ld＞imax时，功率因数随电枢电感变化的关系比较复杂，虽然最大功率因数和电枢电感无关，但速度较低时随着电枢电感的增大而减小，速度较高时则相反。并且电感越小随转速增加功率因数衰减越快。

从图4d 可见，随着电枢电感增大，其去磁因数明显增大。 Ψf/Ld＞imax时只能采用一般弱磁控制，去磁因数小于1；Ψf/Ld＜imax时超过C 点后，如还采用一般弱磁控制去磁因数可能远大于1，而采用最大功率弱磁控制则可将去磁因数限制在1。 因此最大功率因数控制有利于保障永磁材料的安全工作。

图4 电感对电机运行性能的影响Fig.4 Influence of inductance to motor run property

电感越小，转折速度越大，Ψf/Ld＜imax时一般弱磁向最大功率弱磁切换点对应的转速也越高，一般弱磁运行对应的转速范围扩大；Ψf/Ld＞imax时超过基本转速后只能运行于一般弱磁控制，此时电感越小，弱磁控制理想最高转速越小，即一般弱磁运行对应的转速范围变小。

4.3 绕组电阻对运行性能的影响

电枢电阻变化对电机运行性能的影响见图5。 其中第Ⅰ组4 条曲线对应Ψf/Ld＞imax，第Ⅱ组4条曲线对应Ψf/Ld＜imax，电枢电阻均取0，0.5，2.6，5（Ω）4 档变化。

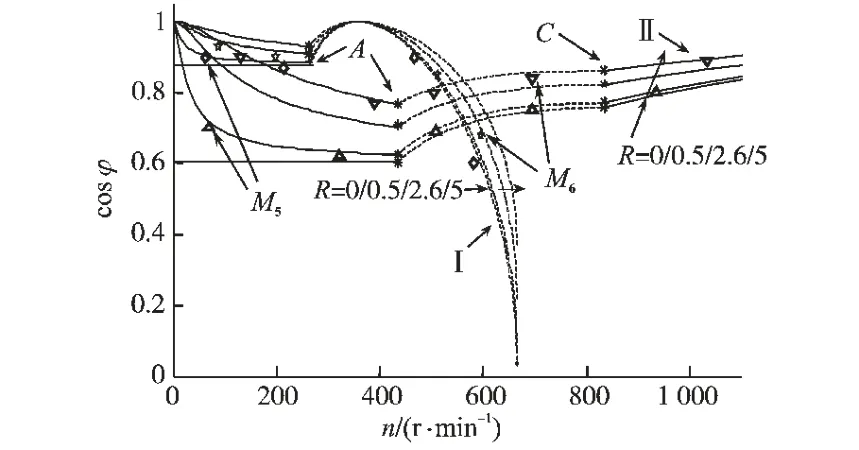
图5 电枢电阻对电机功率因数的影响Fig.5 Influence of armature resistance to power factor of motor

电枢电阻变化时，电机输出转矩、输出功率和去磁因数均不变；由图5可见，无论在恒转矩区还是弱磁区，电枢电阻越大，功率因数就越高。Ψf/Ld＜imax时，随着转速的增大，功率因数先降低，至转折速度时，功率因数最低。 而后随着转速增大，功率因数增大，最终接近于单位功率因数；Ψf/Ld＞imax时，在弱磁区功率因数有1 个极点，不同电枢电阻的电机几乎在同一转速达到单位功率因数，而后随转速增加，功率因数迅速降低。

图3～图5中三角号标出的是物理实验数据，和仿真结果在数据上略有差异，但也证明了以上仿真的正确性。

5 结论

从以上研究可见，伺服电机可以根据转速分段实现全速度范围电流控制策略。 低速区域采取转矩电流比最大控制，中、高速分别采用一般弱磁和最大功率弱磁控制，可以在整个速度范围内增大转矩输出能力，从而扩展有效转速范围。

在采用以上复合控制策略的系统中，中低速区域永磁磁链增大引起电机输出转矩、 功率、功率因数增加，但基本转速、一般弱磁控制理想最高转速均降低。 高速区域永磁磁链增加会引起电机输出转矩、功率、功率因数增加，而不影响理想最高转速；中低速区域电枢电感减小，造成输出功率、功率因数和转折速度的增大，但一般弱磁控制理想最高速度降低。 高速区域电枢电感减小会引起电机输出转矩、功率、功率因数增加，而不影响理想最高转速；电枢电阻增大，输出转矩、功率和去磁因数不变，功率因数有所提高，但同时造成铜耗增大。

对于低速大转矩电机，增大永磁磁链和减小电枢电感是有利的；而对于高速电机，则需要综合配置永磁磁链和电枢电感的大小，使Ψf/Ld略小于imax为佳。电枢电阻的增大会造成电机铜耗增大，在最大功率弱磁运行时更加严重，因此高速电机更应当限制电枢电阻。当然电机参数有很多，它们对于电机运行性能的影响也是很复杂的，在以上的分析中，电机参数的变化范围局限在电机各参数正常设计值附近，因此分析的结果有局限性，但对于电机的参数设计仍然具有指导意义。

[1] 王成元，夏加宽，杨俊友，等.电机现代控制技术[M].北京：机械工业出版社，2006.

[2] 唐任远.现代永磁电机理论与设计[M].北京：机械工业出版社，1997.

[3] Jang Mok Kim，Seung Ki Sul.Speed Control of Interior Permanent Magnet Synchronous Motor Drive for the Flux Weakening Operation [J].IEEE Transactions on Industry Application，1997，33(1): 43-48.

[4] Morimoto S，Takeda Y，Hirasa T.Expansion of Operating Limits for Permanent Magnet Motor by Current Vector Control Considering Inverter Capacity[J].IEEE Transactions on Industry Application，1990，26(5):866-871.

[5] Jahns T M.Flux- weaking Regime Operation of an Interior Permanent-magnet Synchronous Motor Drive[J].IEEE Transactions on Industry Application，1987，23(4):881-889.

[6] Gallegos Lopez G，Gunawan F S，Walters J E.Optimum Torque Control of Permanent-magnet AC Machines in the Field-weakened Region[J].IEEE Transactions on Industry Application，2005，41(4):1020-1028.

[7] Pavel V，Petr B.Interior Permanent Magnet Synchronous Machine Field Weakening Control Strategy-the Analytical Solution[J].IEEE Xplore Restrictions Apply，2008，22(20):753-757.

[8] Verl A，Bodson M.Torque Maximization for Permanent Magnet Synchronous Motors[J].IEEE Transactions on Control Technology，1998，6(6):740-745.

[9] 李长红，陈明俊，吴小役.PMSM 调速系统中最大转矩电流比控制方法的研究[J].中国电机工程学报，2005，25（21）：169-174.

[10] Tursini Marco，Parasiliti Francesco，Zhang Daqing.Real-time Gain Tuning of PI Controllers for High-performance PMSM Drives[J].IEEE Transactions on Industry Applications，2002，38(4):1018-1026.

[11] Morimoto S，Takeda Y，Hatanaka K，et al.Design and Control System of Inverter Driven Permanent Magnet Synchronous Motors for High Torque Operation[J].IEEE Transactions on Industry Applications，1993，29(6):1150-1155.

[12] Morimoto S，Takeda Y，Hirasa T.Servo Drive System and Control Characteristics of Salient Pole Permanent Magnet Synchronous Motor [J].IEEE Transactions on Industry Applications，1993，29(2): 338-343.