基于DSP直流电机模糊免疫PID控制器研究
张小鸣,龙仕玉
(常州大学 信息科学与工程学院,江苏 常州213164)
1 引言
常规数字PID 在数字直流电机调速系统中应用最广,但是PID 参数的整定主要采用试凑法,导致控制性能非优化,控制精度难以提高[1-2]。基于神经网络PID 控制器利用较强的非线性拟合能力实现PID 参数的在线整定和优化[3-5],但需要大量训练样本数据,控制算法较复杂,嵌入式系统实现较困难[6-8]。 模糊PID 控制器利用专家的经验建立PID 整定模糊查询表,具有不依赖于对象模型、控制结构简单、可靠性高、易于工程实现等优点,但控制精度受专家经验影响较大,当电机负载运行或电机受到干扰时,电机的响应速度较慢,很容易出现振荡[9-11]。
生物免疫系统反馈机制实际上就是一个自适应非线性P 控制器,能逼近非线性函数[12-13]。 模糊免疫PID 控制器把非线性P 控制器与模糊PID相结合,克服了模糊PID 控制器在强干扰或具有高度非线性和不确定性时调节随动性差的缺点,大大改善了控制器的性能。在基于DSP 的直流电机控制试验平台上构建模糊免疫PID 控制模块进行样机试验,试验表明系统的控制品质具有良好的动态指标,基本实现无超调输出。
2 模糊免疫PID 控制器设计原理
免疫控制器原理实际上就是一个非线性P(比例)控制器,P 的控制器输出相当于抗原刺激的T 细胞输出TH(k),外来干扰TS(k)相当于细菌,根据免疫系统的免疫原理,免疫系统要产生抗原来吞噬入侵外来干扰源即细菌,因此免疫系统产生的输出为

其中

式中:ε(k)为第k 代抗原数量;k1,k2为比例常数;f(·)为一个非线性函数。
以抗原的数量ε(k)作为非线性P 控制器控制误差e(k),免疫系统总刺激S(k)作为控制器输入u(k),则有如下的反馈控制规律:
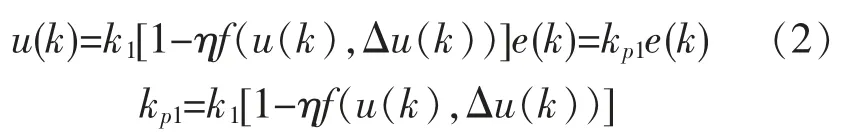
式中:k1为控制反应速度;η 为控制稳定效果,η=k2/k1。
f(u,△u)采用模糊控制器非线性逼近,即每个输入变量模糊化为一个模糊集合,取两种值:分别是“正”(P)和“负”(N);每个输出变量模糊化为一个集合,取3 个值,分别是“正”(P),“零”(Z)和“负”(N)。 以上隶属函数都定义在整个(+∞,-∞)区间。 模糊控制器可采用以下4 条逼近非线性函数f(u,△u)规则:

采用查德[14](Zadeh)的模糊逻辑与(AND)操作,并采用常用的求最大隶属度平均法来得到模糊控制器的输出f(u,△u)。
由于非线性P 控制器不能消除积分累计误差,因此,需要结合PID 控制器组成模糊免疫PID控制器,定义控制误差为

式中:error(k)为第k 次采样误差;rin(k)为第k次采样输入;yout(k)为第k 次采样输出。采用增量式PID 控制器,其3 项输入为

PID 输出控制算法为

式中:kp,ki,kd分别为比例系数、 积分系数和微分系数。

将PID 控制器输出U 作为免疫反馈模型中的外界物质即抗原量ε(k),则得到模糊免疫PID控制器,其比例系数为

其控制算法表示为

当k1增大时,响应的速度会加大,系统快速性会变好,η 增大时,系统超调量会减小,相对稳定性会变好,合理的整定k1和η 能使控制系统具有较短的响应时间和超调量。 模糊免疫PID 控制框图如图1所示。
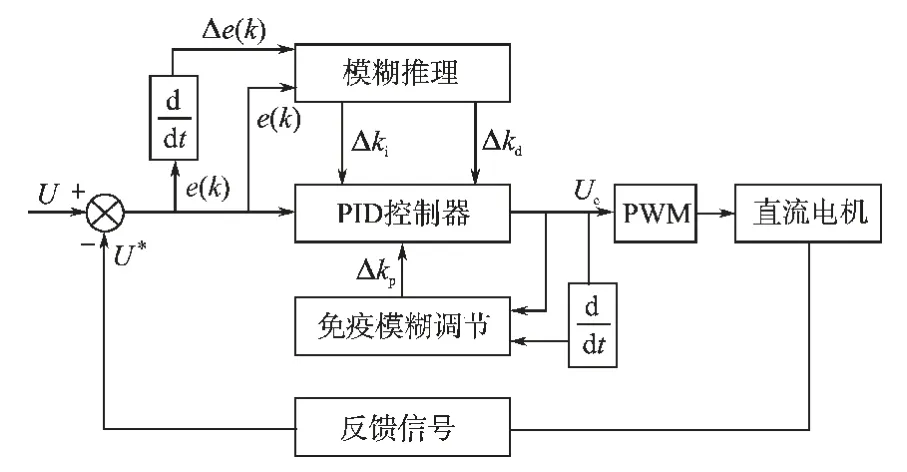
图1 模糊免疫PID 控制器框图Fig.1 Block diagram of fuzzy immune PID controller
模糊免疫PID 控制器以反馈信号与给定信号之差e 和误差变化率△e 作为模糊控制器的输入量,经过模糊推理和决策后更新ki,kp值,即得到PID 控制器输出量Uc,Uc和其变化率作为免疫调节器的输入,经过免疫环节调节后产生新的P变化量(△KP),再送给PID 控制器更新KP,PID 控制器再产生新的Uc,用这种闭环不断优化的Uc去控制直流电机。
3 模糊免疫PID 试验系统模型
直流电机传递函数为

式中:Ue为电枢额定电压;Ie为电枢额定电流;R为电枢电阻;J 为电机转子转动惯量;ne为额定转速;B 为电机和负载的粘性阻尼系数;La为电枢电感,Φ 为励磁磁通量;CT为转矩系数;Ce为电机电势系数。
对直流电机传递函数进行Z 变换,其差分方程为
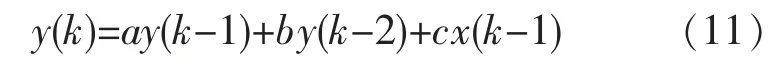
其中

式中:T 为采样周期。
试验所用稀土调速直流伺服电机,铭牌参数如下:额定功率Pe=0.2 kW,额定电压Ue=48 V,额定电流Ie=5.2 A,额定转速ne=1 500 r/min。转动惯量J=3.527×10-3kg·m2,电枢电感La=2 mH,电机电枢内阻R=1.2 Ω,额定转矩1.2 N·m。
试验系统采用双闭环,外环为位置环,内环为电流环,位置环采用模糊免疫PID 控制,电流环采用PI 控制,位置环和电流双闭环结构框图如图2所示。

图2 位置环和电流环结构框图Fig.2 Block diagram of speed and current control loops
模糊免疫PID 算法主程序调用模糊免疫PID控制算法子程序运算得出控制量Uc(k),把Uc(k)作为直流电机差分方程式(11)的输入,最后调用稀土直流伺服电机差分方程产生系统输出响应。主程序流程图如图3a 所示。 模糊免疫PID 算法子程序流程图如图3b 所示。
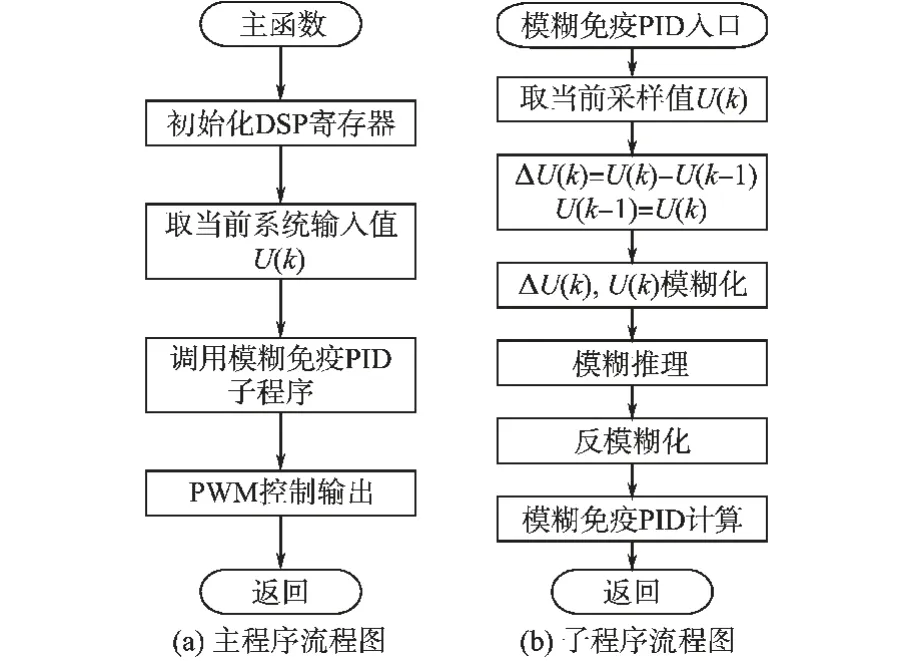
图3 模糊免疫PID 控制程序流程图Fig.3 The main of fuzzy immune PID control algorithm flow chart
4 试验结果
以TI 公司的数字信号处理器TMS320LF2407为控制器对稀土直流伺服电机进行试验,试验采用H 桥驱动。 位置反馈采用码盘,DSP 捕获码盘计数脉冲,并计算出位置误差和误差变化率作为控制器输入,在事件单元(EVA)转化为占空比不同的方波来实现对电机的控制。
模糊免疫PID 算法优化出位置环PID 参数为:kp=368.1,ki=10.4,kd=2 040。 电流环优化出PI参数为:kp=3.375,ki=0.607 5。PWM 输出频率为2 kHz,电流环采样周期为10 μs,位置环采样周期为1 ms。 编码器为1 000 线。
试验方法为:加速度1 000 rad/s2,加加速度40 000 rad/s3,目标速度1 000 r/min,负载1 N·m。采用S 型位置参考曲线控制电机,电机运动轨迹为先正向运行60 rad,等待100 ms 后再反向运行60 rad,依次循环。上位机采用Labview 编写,通过串口与DSP 进行通信,将DSP 测试数据传送到Labview 界面上连续显示。随机截取Labview 控制界面上伺服系统在免疫PID 算法和模糊免疫PID算法下的参考位置与实际位置、参考速度与实际速度响应曲线,分别如图4和图5所示。 从图4和图5可看出,左边一栏记录数据是实际测试值,右边一栏记录数据是参考设置值,由此可得出系统跟随误差分析结果如表1所示。

表1 系统测试误差分析结果Tab.1 System testing error analysis results
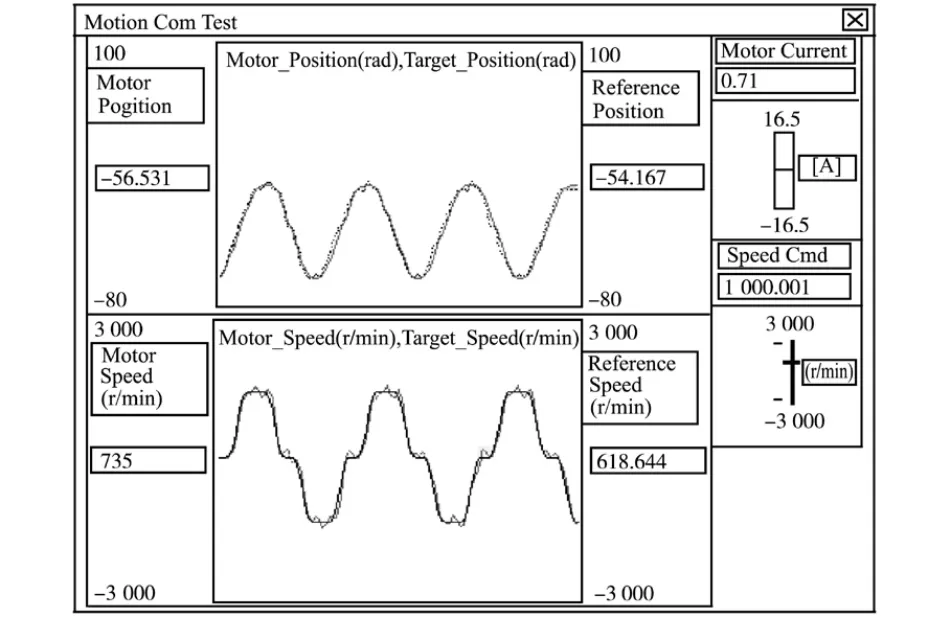
图4 模糊PID 控制器下带负载的位置和速度响应曲线Fig.4 The position and speed response graph under fuzzy PID controller with loads

图5 模糊免疫PID 控制器下带负载的位置和速度响应曲线Fig.5 The position and speed response graph under fuzzy immune PID controller with loads
由表1可知,在S 型位置参考曲线模式下运行,模糊PID 控制器位置跟随误差最大约为4.3%。 在电机到达最大正负位置或者换向时有很大振荡和噪声。 而模糊免疫PID 控制器的位置跟随误差大大减小,最大约为0.023%,基本上准确到位,而且定位过程平稳不过冲。 因此,模糊免疫PID 控制器具有较好的动态跟随性,电机加速或者减速时间短,而且在任意位置运行平稳无噪声,可大大减缓柔性冲击,保持较高的控制精度。
5 结论
模糊免疫PID 控制利用免疫反馈机制对PID参数进行在线自适应调整,实现了PID 参数的优化。基于DSP 的模糊免疫PID 控制器样机试验表明:模糊免疫PID 控制器既继承了模糊PID 控制器适用于数学模型不确定被控对象,实现简单,对过程参数变化不敏感的优点,又克服了模糊PID 控制非线性系统随动性差的缺点,较好地实现了对直流伺服电机的速度控制。 通过与模糊PID 控制器比较试验,发现模糊免疫PID 控制器跟随误差明显小于模糊PID 控制器,动态过程更加平滑。
[1] 符晓玲,姜波.基于DSP 的数字PID 控制器设计[J].现代电子技术,2007,30(7):129-131.
[2] 张立丽,李亮,史小华.基于PIC 芯片嵌入式电机控制器的研究[J].现代电子技术,2009,32(9):164-167.
[3] Kim Kyeone-hwa,Youn Myung-joong.DSP-based High-speed Sensorless Controll for a Brushless DC Motor Using a DC Link Voltage Control [C]∥Electric Power Components and Systems,2002,30:889-906.
[4] Hany M Hasanien.FPGA Implementation of Adaptive ANN Controller for Speed Regulation of Permanent Magnet Stepper Motor Drives [J].Energy Conversion and Management,Energy Conversion and Management,2011,52 (2):1252-1257.
[5] 李先祥,徐小增,肖红军.基于小波神经网络控制的无刷直流电机调速系统[J].中国电机工程学报,2005,25(9):126-129.
[6] 张咏军,王航宇.基于BP 神经网络的温度模糊PID 控制器设计[J].现代电子技术,2008,31(7):133-135.
[7] 马宁.自适应神经模糊-PID 控制在电厂过热汽温控制中的应用[J].自动化技术与应用,2008,27(4):31-33.
[8] 杨原青,刘卫东,李乐.基于自适应模糊PID 算法的切纸机伺服控制器设计[J].微特电机,2010,38(3):55-58.
[9] 周黎英,赵国树.模糊PID 控制算法在恒速升温系统中的应用[J].仪器仪表学报,2008,29(2):405-409.
[10] 王凌,刘卫国.基于模糊PI 控制的无刷直流电机调速系统仿真[J].计算机仿真,2009,26(10):186-189.
[11] 魏星,刘琨,王亚军.模糊免疫自适应控制系统的Matlab 仿真研究[J].电力自动化设备,2005,25(5):34-36.
[12] 李广军,崔继仁,党建亮.基于模糊免疫PID 控制的恒压供水系统研究[J].煤炭技术,2011,30(7):33-34.
[13] 夏长亮,刘丹,王迎发,等.基于模糊规则的无刷直流电机免疫PID 控制[J].电工技术学报,2007,22(9):68-73.
[14] 谢仕宏.MATLAB R2008 控制系统动态仿真实例教程[M].北京:化学工业出版社,2009.