基于自适应噪声消除的无差拍控制方法

王宗臣，包志华，张士兵，施博一

（1.南通大学 电子信息学院，江苏 南通226007；2.江苏现代电力电容器有限公司，江苏 南通226005）

1 引言

近年来，各种电力电子设备在配电网中得到了不断应用，但这些负荷的冲击性、非线性和不平衡性的用电特征对电网造成了严重的谐波污染。 采用有源电力滤波器（APF）清除谐波污染成为提高配电网中电能质量的重要趋势。而电流控制方法，即如何控制逆变器功率器件的开关状态，使输出电流能够准确、 快速地跟踪参考电流，是决定有源电力滤波器性能的关键之一。 目前，有源电力滤波器的电流控制方法主要有两大类[1]：一种是传统的控制方法，如单周期控制、滞环控制等。 单周期控制电路简单，但存在电流纹波，从而产生电流直流分量；滞环控制的开关频率、损耗和控制精度受滞环宽度的影响。 二是新型智能控制，如无差拍控制、模糊控制、人工神经网络控制等。智能控制控制精度高但计算量比较大，不利于工程实现。 随着微处理器性能的不断提高，高速数字信息处理器的应用使得一些智能控制方式成为可能。其中无差拍控制具有动态响应快，控制精度高，易于数字实现，便于工程应用等优点，具有广阔的应用空间。

无差拍控制利用前一时刻的参考电流和补偿电流，预测下一时刻的参考电流值以获得电流误差最小的开关状态，使实际输出电流准确、快速跟踪参考电流[2-4]。 其控制方式一般是控制逆变器输出的平均电压，使有源电力滤波器输出电流跟踪参考电流。 但无差拍控制在对瞬时电流进行处理控制时易受噪声的干扰，影响跟踪精度； 同时，采样以及计算造成的控制延时影响系统稳定性[5]。 在现有无差拍控制文献中对噪声抑制的研究比较少见。 文献[6]在硬件上使用可复位积分器作为输入滤波器对输入信号中的噪声进行抑制，但未对参考电流进行预测，因而还是存在采样及计算造成的控制延时。 如果能够预测参考电流使控制算法提前执行就可以消除时延。 目前参考电流信号的预测方法主要有线性预测[2]、重复预测[7-9]、自适应预测[10-11]等。 线性预测方法简单，计算量小，但效果较差； 重复预测精度高，但动态响应速度相对较慢，而且这些预测方法易受噪声的干扰。 自适应预测易于数字实现，具有较强的自适应能力，与较好的使用价值。

针对无差拍控制易受噪声干扰的问题，本文提出一种应用于并联有源电力滤波器的基于自适应噪声消除的无差拍控制方法。 该方法利用改进的基于预测原理的自适应噪声消除算法处理不同周期但同一相位的采样数据，自适应预测参考电流、输出电流和系统电压以消除噪声的影响。

2 无差拍控制策略

2.1 单相并联有源电力滤波器主电路结构

单相并联有源电力滤波器投切方便灵活、不会对系统运行造成影响，在电网中可以等效为一个受控电流源，并且较三相并联有源电力滤波器具有效率高、结构简单、体积小、保护简单的优点。 图1为单相并联有源电力滤波器的主电路等效结构图。 该结构采用电解电容作为直流侧储能元件，S1，S2，S3，S44 个IGBT（insulated gate bipolar transistor）构成逆变器，并通过电抗器并联到电网中。 图1中us(t)为电网相电压，uc(t)为逆变器输出电压，udc为直流侧电容电压，R 为电抗器等效电阻，is(t)为系统电流，iL(t)为非线性负载电流，ic(t)为有源电力滤波器输出电流。

图1 单相并联有源电力滤波器主电路等效结构图Fig.1 Main equivalent circuit of single phase parallel active power filter

2.2 无差拍控制模型

根据图1所示的单相并联有源电力滤波器主电路等效结构，得到电路方程

解式（1）得：

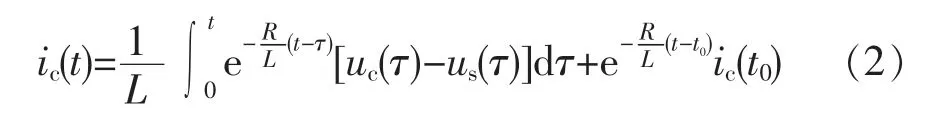
由于功率器件IGBT 的开关频率fs可达10 kHz，远远大于系统电压的频率，可认为uc(t)和us(t)在一个采样周期内不变，则上式可写为

式中：uc(k)，us(k)分别为k 时刻uc(t)，us(t)的采样值；ic(k+1)，ic(k)分别为k+1，k 时刻有源电力滤波器输出电流。

如果采用对称PWM 信号控制IGBT 通断，则在一个采样周期内有

式中：td(k)为IGBT 在一个采样周期内的开通时间。uc(t)在kT～(k+1)T 内的平均值为

得

根据采样控制理论中一个重要结论：冲量相等而形状不同的窄脉冲加在具有惯性的环节上时，其效果基本相同。用(k)替代uc(k)并由式（5）、式（6）可得输出脉冲时间td(k)，即

为了准确跟踪参考电流信号，消除采样以及处理器计算造成的控制时延，需要在第k-1 个采样周期内预测系统电压u*s(k)、输出电流i*c(k)、参考电流(k+1)以取代式（7）中的系统电压us(k)、输出电流ic(k)及输出电流ic(k+1)，使控制算法提前一拍执行，如图2所示。 这样，第k 个采样周期的td(k)为

图2 无差拍控制示意图Fig.2 Deadbeat control schematic diagram

3 基于自适应噪声消除的无差拍控制方法

3.1 自适应噪声消除原理

自适应滤波器噪声消除是利用自适应滤波器具有在未知环境下良好运行并跟踪输入统计量随时间变化的能力，通过不断调整抽头权系数来适应发生变化的信号和噪声的统计特性，达到消除噪声干扰的目的[12]，如图3所示。

图3 基于预测原理的自适应噪声消除Fig.3 Adaptive noise cancellation based on principles of prediction

考虑到白噪声在时间上具有不相关性，图3中将受白噪声干扰的输入信号x(k)延迟一定的时间，作为自适应滤波器的输入信号x′(k)，并且将带噪声的输入信号作为期望信号d(k)。 由于有用信号在延迟后具有很强的相关性，可以对该信号进行自适应估计，而噪声在抽样点上是不相关的，自适应滤波器不能对白噪声进行估计，因此输出信号中噪声会减小，y(k)是对d(k)中有用信号的最佳估计。

3.2 自适应噪声消除无差拍控制算法

为消除控制时延对系统稳定性的影响，无差拍控制需要对参考电流进行预测，由此得到自适应噪声消除方法的改进方案，如图4所示，其中图4a 为参考电流(k+1)预测算法结构，图4b 为输出电流i*c(k)或系统电压u*s(k)预测算法结构。 图4中N 为一个基波周期内的采样数，各FIR 滤波器均相同（权系数个数为M）。

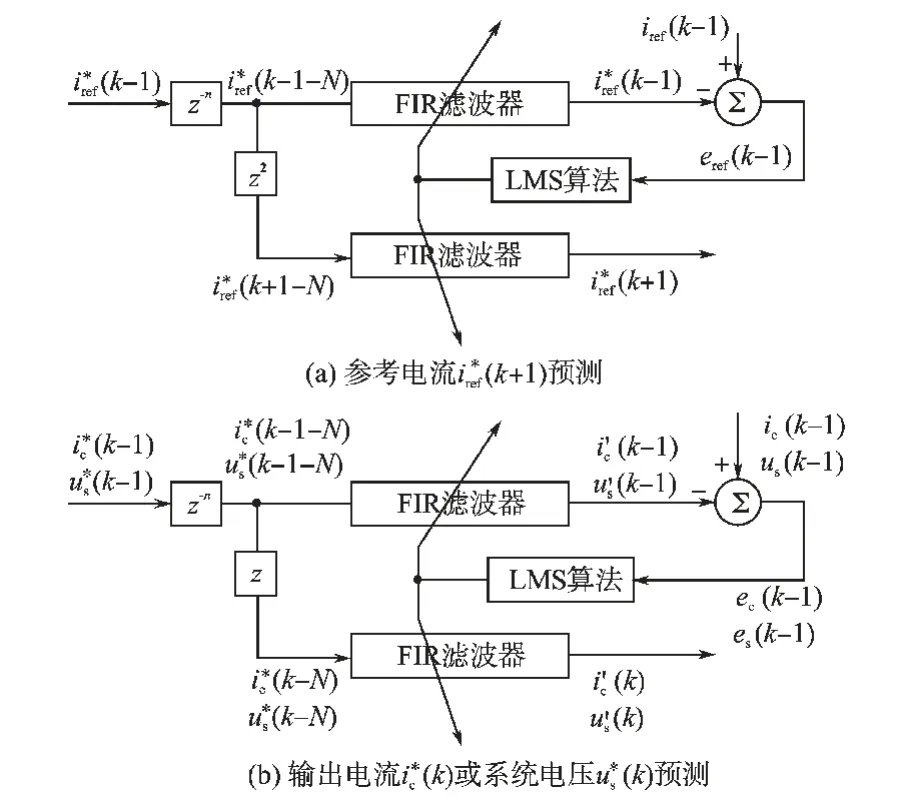
图4 改进的基于预测原理的自适应噪声消除Fig.4 Improved adaptive noise cancellationbased on principles of prediction

在图4a 中，由于参考电流iref(k)具有较强的周期性和重复性的特点，不同基波周期同一相位的信号具有较强的相关性，因此可以将作为输入信号，iref(k-1)作为(k-1)的期望信号。输入信号˙iref(k-1) 延迟N 个采样周期后得到延迟信号˙iref(k-1-N) ，将其输入FIR 滤波器中进行处理，同时iref(k-1)与输出信号(k-1)的误差eref(k-1)作为反馈量经LMS 算法处理调节滤波器权值系数。 由于(k-1) 和(k-1-N) 中的有用信号具有很强的相关性，而噪声不具有相关性，FIR 滤波器对有用信号进行自适应估计，而不能够对噪声进行估计，因而输出信号(k-1)是对iref(k-1)中有用信号的最佳估计。由于2 个FIR 滤波器相同，并均由eref(k)调节权值系数，因此输入信号i˙ref(k+1-N)经自适应估计后的输出信号(k+1)也是2 个采样周期后参考电流iref(k+1)中有用信号的最佳估计。

考虑到定步长LMS 算法无法兼顾收敛速度和稳态失调，采用变步长LMS 算法对FIR 滤波器的权系数进行更新。 预测参考电流(k+1)的迭代公式为

α，β 的选取应根据初始误差的大小来选择，使初始误差对应的步长尽可能大[13]。

为确保该算法的稳定性，步长μ 应有一定的范围，因此在递推过程中，对步长进行限幅，

式中：μmax值应能保证算法的稳定性，通常取接近定步长LMS 算法的临界稳定步长值；μmin的值应当兼顾收敛速度和稳态失调的要求，一般为一个比较小的正值。

同理，对输出电流i*c(k)、系统电压u*s(k)的预测可以采用类似的方法，如图4b 所示，输入信号为

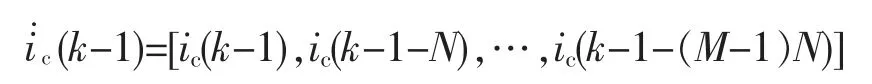
或者

参考向量为ic(k-1)或者us(k-1)。输出信号i*c(k)，u*s(k)分别是一个采样周期后输出电流ic(k)、系统电压us(k)中有用信号的最佳自适应估计。 预测输出电流i*c(k)或系统电压u*s(k)的迭代公式为

4 仿真结果及分析

为了检验提出的控制方法的动态响应速度、跟踪精度和对噪声干扰的敏感度，采用Matlab 软件在单相并联有源电力滤波器基础上进行仿真，仿真主电路结构如图1所示，参数设定为：us(t)=200sin(2πft) V，f=50 Hz，udc=400 V，R=1 Ω，采样周期Ts=0.000 1 s，N=200，L=0.5 mH，M=4，α=1，β=1，μmin=10-3，μmax=10-1。 取负载电流：

则参考电流：

并对传统自适应预测无差拍控制算法[11]和本文提出的基于自适应噪声消除的无差拍控制算法进行仿真比较。

图5所示的是输出电流与参考电流的误差比较。可以看出，虽然两种算法的输出电流与参考电流的误差波形在初始时刻都在一个基波周期后稳定，但基于自适应噪声消除的无差拍控制算法的误差波形稳定后几乎为零。 表1列出了输出电流稳定后系统电流中各次谐波幅值比较。 显然，基于自适应噪声消除的无差拍控制算法得到的系统电流中各次谐波幅值接近于零。 其中传统自适应预测无差拍控制算法得到的系统电流总畸变率为3.112 6%，而基于自适应噪声消除的无差拍控制算法得到的系统电流总畸变率为0.002 4%。

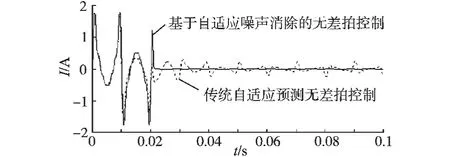
图5 输出电流与参考电流的误差比较Fig.5 Comparison of error between output current and reference current

表1 电流稳定时系统电流各次谐波幅值比较Tab.1 Comparison of harmonic amplitude of system current while load current is fixed

为验证两种算法对噪声干扰的敏感程度，对负载电流叠加信噪比10 dB 的白噪声，仿真结果如图6所示。 从图6中明显看出，基于自适应噪声消除的无差拍控制算法的输出电流受噪声干扰的影响程度要比传统自适应预测无差拍控制算法较小。

图6 带噪声时输出电流比较Fig.6 Comparison of output current with noise

图7验证了基于自适应噪声消除算法的动态响应速度。 基于自适应噪声消除算法在0.2 ms时使参考电流突增一倍。 由此可知，基于自适应噪声消除的无差拍控制算法的输出电流比传统的自适应预测无差拍控制算法能够在很短的时间内达到稳定状态。

图7 负载电流突变时输出电流比较Fig.7 Comparison of output current while load current is suddenly changed

5 结论

本文根据参考电流具有较强的周期性和重复性的特点，提出一种应用于并联有源电力滤波器的无差拍控制方法。 该方法有效地抑制了在对瞬时电流进行处理时的噪声干扰，消除了控制时延对系统稳定性的影响，具有良好的动态响应速度、跟踪精度和系统稳定性。 仿真结果证明了该算法的有效性和可行性。

[1] 王伟，周林，徐明.有源电力滤波器控制方法综述[J].继电器，2006，34（20）：81－85.

[2] 曾繁鹏，谭光慧，伏祥运，等.有源电力滤波器的简单无差拍控制策略[J].电气应用，2006，25（8）：60－63.

[3] Gokhale K P，Atsuo Kawamura，Hoft R G.Deadbeat Micropro -cessor of PWM Inverter for Sinusoidal Output Waveform Synthesis[J].IEEE Transactions on Industry Applications，1987，23（5）：901－909.

[4] 蒯松岩，代尚方，吴涛，等.基于电流无差拍控制的PWM整流器[J].电气传动，2011，41（9）：23－25.

[5] Hung G K，Chang C C，Chen C L.Analysis and Implementation of a Delay- compensated Deadbeat Current Controller for Solar Inverters[J].IEE Proc.Circuits，Devices and Systems，2001，148（5）：279－286.

[6] 周荔丹，解大，Khan M M，等.单相并联有源滤波器的鲁棒电流控制方法 [J].电力系统自动化，2005，29（23）：44－48.

[7] 何英杰，刘进军，王兆安，等.基于重复预测原理的三电平APF 无差拍控制方法[J].电工技术学报，2010，25（2）：114－121.

[8] 唐健，王翔，何英杰，等.三相四线制有源滤波器新型无差拍控制[J].电力系统自动化，2007，31（19）：59－62.

[9] 韩郁，詹长江，赵良炳，等.三电平并联型电能质量调节器的控制技术研究[J].清华大学学报，2000，40（3）：40－43.

[10] Nishida K，Rukonuzzman M，Nakaoka M.Advanced Current Control Implementation with Robust Deadbeat Algorithm for Shunt Single- phase Voltage - source Type Active Power filter[J].IEE Proc.Electric Power Application，2004，151（3）：283－288.

[11] 李东伟，秦兵才.基于自适应预测算法的谐波电流无差拍控制[J].电气技术，2009（6）：26－27.

[12] Greenberg J E .Modified LMS Algorithms for Speech Processing with an Adaptive Noise Canceller[J].IEEE Trans.on Speech and Audio Processing，1998，6（4）：338－351.

[13] 高鹰，谢胜利.一种变步长LMS 自适应滤波算法及分析[J].电子学报，2001，29（8）：1094－1097.