模糊控制的扰动观察法在光伏MPPT中的应用
李春玲,石季英,武艳辉,王成山
(天津大学 电气工程及自动化学院,天津300072)
1 引言
在能源危机日益突出的环境下,太阳能光伏并网发电技术在近30年得到了越来越多的关注[1]。
由于光伏电池的输出电压和输出电流随着光照和温度的变化具有强烈的非线性,因此在特定环境下存在着一个唯一的最大功率输出点(MPP)。在实际的应用系统中,为了在同样的日照强度和温度下提高光伏发电系统的转换效率,就存在着一个最大功率输出点跟踪 (MPPT)的问题。 常用的MPPT 算法已有很多种[2-3],如恒电压跟踪法(CVT)、扰动观察法(P&O)、电导增量法(INC)等。这些算法有各自的缺点,CVT 控制精度不高。P&O 法和INC 的缺陷在于由于采用定步长方式,难以兼顾跟踪的响应快速性以及系统的稳定性两方面的要求[4]。
针对上述传统方法的缺点,近年来又将智能控制引进MPPT 算法中[5-7]。 为了实现提高跟踪速度、减少MPP 附近功率振荡的目标,本文提出了一个智能控制技术——模糊控制的扰动观察法(P&O)的光伏MPPT 控制方案。 文章详细地介绍了光伏发电系统,并在Matlab/Simulink 中建立了光伏电池,模糊控制的P&O 的MPPT、产生占空比的PWM 模块以及Boost 变换器的仿真模型。文中在光照1 000 W/m2和温度25 °C 环境下,将模糊控制的P&O 与传统的P&O 进行了对比,通过仿真验证了模糊控制的P&O 的正确性与优势性。
2 光伏发电系统
光伏发电系统包括光伏电池、MPPT 控制器、PWM 模块、Boost 变换器以及负载。 如图1所示。光伏电池的功率经Boost 变换器传输至负载。 光伏电池的输出电压U 和输出电流I 采样至MPPT控制器来控制跟踪光伏电池的最大功率。 MPPT控制器通过光伏电池的输出电压和输出电流调节产生扰动电压Uref从而不断控制光伏电池电压使其达到MPP 的最优电压。 扰动电压Uref作为PWM 模块的输入量产生输出信号为0-1 变化的占空比D。PWM 模块的输出占空比D 是Boost 变换器的输入信号。

图1 光伏系统Fig.1 PV system
2.1 光伏电池工程实用模型的建立
光伏电池的等效电路如图2所示。

图2 光伏电池等效电路Fig.2 Equivalent circuit for PV cell
按照图1中的电流、电压参考方向,可以得到光伏电池的I-U 特性方程:

式中:Iph为光生电流,A;I0为二极管反向饱和电流,A;q 为电子电荷;T 为绝对温度,K;K 为玻尔兹曼常数;A 为二极管因子常数;Rs为串联等效电阻,Ω;Rsh为并联等效电阻,Ω;I 为电池输出电流,A;U 为电池输出电压,V。
式(1)中的5 个主 要参数,即Iph,I0,Rs,Rsh和A,与电池温度和日照强度相关,既难以确定也不是厂商提供的标准参数,因此不便于工程应用。若在式(1)基础上,做两点近似[8],便可以得到光伏电池的实用I-U 方程:

基于上述工程实用模型,Matlab/Simulink 中搭建模块仿真,得到的光伏电池的特性如图3所示。 由图3可以看出光伏电池是一个既非恒压源又非恒流源的非线性直流电源。 光伏电池的最大功率是唯一的,为了使光伏电池能量转换效率最大化,必须进行最大功率跟踪(MPPT)。
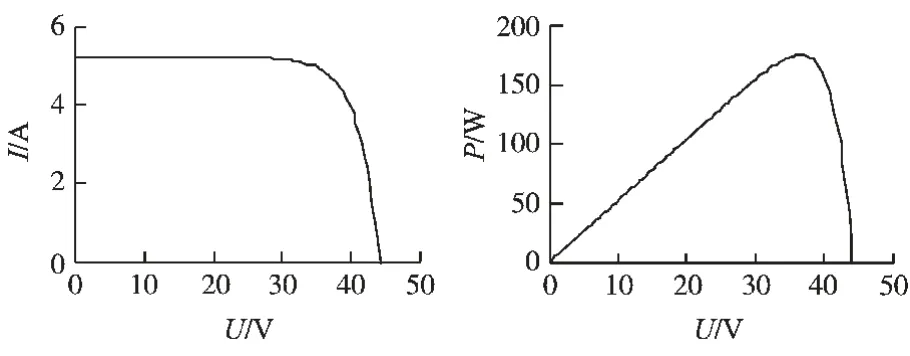
图3 光伏电池的特性Fig.3 The characteristic of PV Cell
2.2 模糊控制的P&O 的MPPT
模糊控制的P&O 核心是模糊逻辑控制器(fuzzy logic controller),模糊控制的P&O 实际是对定步长的传统的P&O 的改进,控制方法是根据光伏电池的实时输出功率调整扰动步长,使光伏电池工作在最大功率点附近。
模糊控制的P&O 的仿真模型如图4所示,控制器的输入为控制误差e 和误差变化率ce 为

输出为第k 时刻的新的步长值。

图4 模糊控制的P&O 的MPPT 模型Fig.4 Fuzzy control based P&O MPPT model
控制策略如下。
1)当e>0,ce>0 时,新步长应为正值。
2)当e>0,ce<0 时,新步长可不变。
3)当e<0,ce>0 时,新步长可不变。
4)当e<0,ce<0 时,新步长应为负值。
5)当最大功率与当前功率相差较大时,采用较大步长以加快系统的响应速度,当最大功率与当前功率相差较小时,采用较小的步长以降低扰动的幅度,减少功率损耗。
根据以上控制策略,e 和ce 的模糊论域为[-5,5],分别有7 个和5 个模糊子集;Uref论域为[-15,15],有5 个模糊论域。 e=[NB,NM,NS,ZE,PS,PM,PB],ce=[NB,NS,ZE,PS,PB],Uref=[NB,NS,ZE,PS,PB]。
根据光伏电池特点,选三角形隶属度函数的形状。e,ce 和Uref的隶属度函数如图5所示,然后根据控制策略得出模糊控制规则。 解模糊采用的是Centroid 面积中心法。

图5 隶属度函数的形状Fig.5 The shape of the membership functions
2.3 PWM 模块
PWM 模块(见图6)是将MPPT 模块的输出步长值作为输入量,输出是Boost 变换器的占空比。

图6 PWM 模块Fig.6 PWM model
2.4 Boost 变换器
Boost 变换器的仿真电路如图7所示,负载电压U0、输入电压Uin和占空比D 之间的关系为

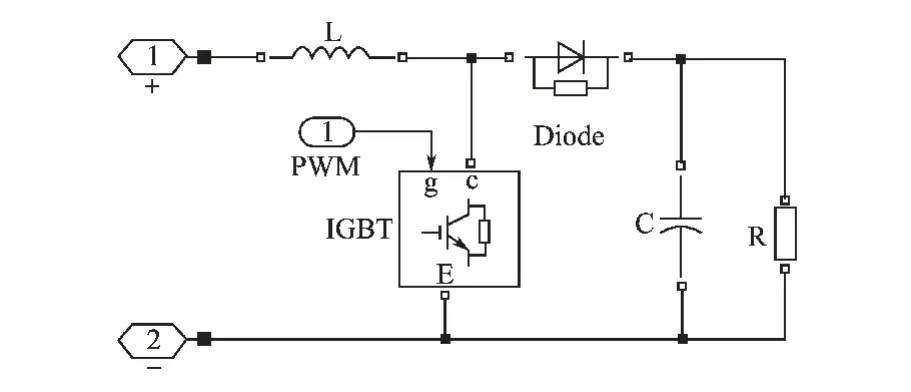
图7 Boost 变换器仿真模型Fig.7 Simulation model of boost converter
3 仿真结果
在Matlab/Simulink 环境中对模糊控制的P&O 的MPPT 进行仿真验证。 在相同光照1 000 W/m2和温度25 °C 环境下与传统的P&O 仿真对比,仿真时间均为0.4 s,采用ode23tb 算法,仿真结果光伏电池输出功率P 见图8,输出电压U 见图9,输出电流I 见图10。
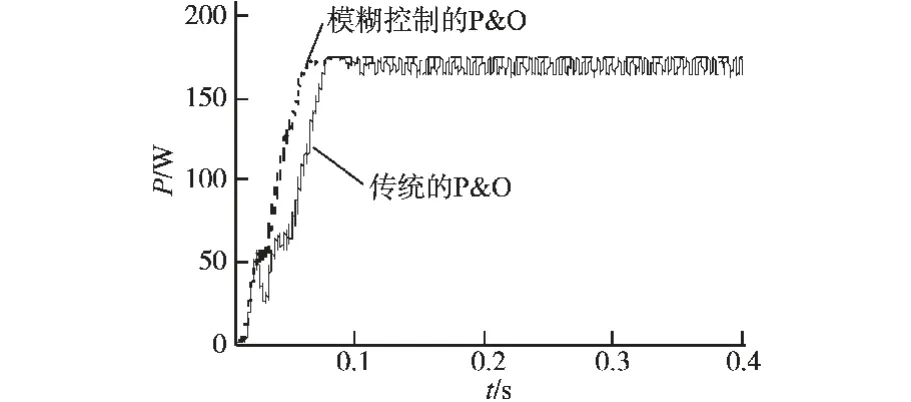
图8 光伏电池输出功率对比图Fig.8 Comparison diagram of PV cell output power

图9 光伏电池输出电压对比图Fig.9 Comparison diagram of PV cell output voltage

图10 光伏电池输出电流对比图Fig.10 Comparison diagram of PV cell output current
由图8~图10可见,采用模糊控制的P&O 的MPPT 经过0.065 s 跟踪逐渐达到稳定,输出功率达到最大值175.66 W 近似等于额定输出功率176 W,输出电压、电流几乎没有振荡。 而传统的P&O 法经0.1 s 跟踪才逐渐达到稳定,与模糊控制的P&O 对比其输出功率电压、 电流振荡比较大。通过图11光伏电池输出功率的对比放大图可以更加明确看到稳态时,P&O 的振荡范围为162 ~175.66 W,而模糊控制的P&O 几乎没有振荡。 但是由于模糊控制的P&O 也属于动态自寻优法,达到最大功率点也会有略微的振荡,但是其振荡是很小的,振荡范围只有175.55~175.66 W。 模糊控制的P&O 放大图12可以说明这一点。 由以上分析可知模糊控制的P&O 具有更好的性能。
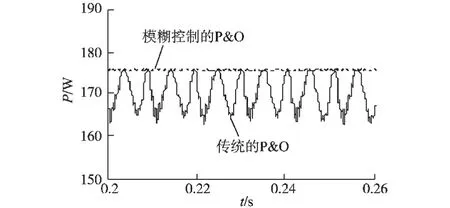
图11 光伏电池输出功率对比放大图Fig.11 Comparison enlarged diagram of PV cell output power
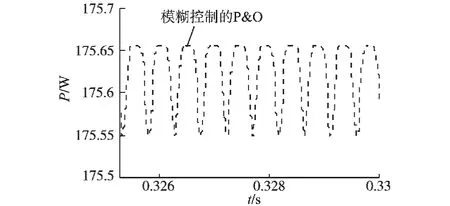
图12 模糊控制的P&O 输出功率放大图Fig.12 Enlarged diagram of output power with fuzzy control based P&O
由于功率振荡的幅度与扰动步长的大小有关,由图13可知模糊控制的P&O 的扰动步长在光照稳定后几乎不变,而P&O 的步长则是在最优值的附近波动,因而会造成较大的功率振荡,导致功率损失。 故模糊控制的P&O 的功率振荡远远小于传统的P&O 功率振荡幅值。
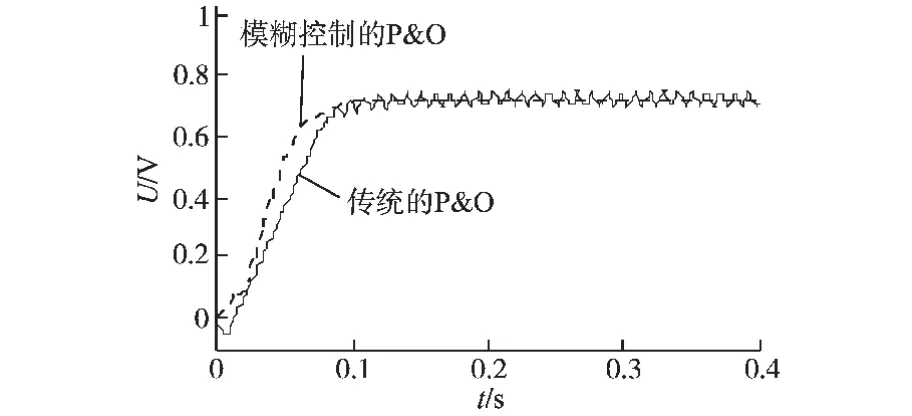
图13 扰动步长Uref对比图Fig.13 Comparison diagram of the perturbed voltage Uref
4 结论
本文在Matlab/Simulink 中对光伏系统的模糊控制的P&O 的MPPT 进行了建模分析,模拟了在光照为1 000 W/m2和温度25 °C 环境下,将模糊控制的P&O 的MPPT 与传统的P&O 进行了较为全面的仿真对比分析。仿真结果表明,模糊控制的P&O 的MPPT 具有响应速度快、稳态振荡小的特点,较好地解决了传统的P&O 方法的不足,能够最大程度地提升系统效率、降低功率损失。
[1] 王飞,余世杰,苏建徽,等.太阳能光伏并网发电系统的研究[J].电工技术学报,2005,20(5):72-74.
[2] 周林,武剑,栗秋华,等.光伏阵列最大功率点跟踪控制方法综述[J].高电压技术,2008,34(6):1145-1153.
[3] 崔岩,蔡炳煌,李大勇,等.太阳能光伏系统MPPT 控制算法的对比研究[J] .太阳能技术,2006,27(6):535-538.
[4] 蔡明想,姜希猛,谢巍.改进的电导增量法在光伏系统MPPT中的应用[J].电气传动,2011,41(7):21-24.
[5] Mellit A,Kalogirou S A.Artificial Intelligence Techniques for Photovoltaic Applications[J].Progress in Energy and Combustion Science,2008,34(5),574-632.
[6] Chin C S,Neelakantan P,Yoong H P,et al.Fuzzy Logic Based MPPT for Photovoltaic Modules Influenced by Solar Irradiation and Cell Temperature[C]∥2011 UKSim 13th International Conference on Modeling and Simulation,2011:130-137.
[7] Subiyanto,Mohamed A,Hannan M A.Maximum Power Point Tracking in Grid Connected PV System Using a Novel Fuzzy Logic Controller[C]∥Proceedings of 2009 Student Conference on Research and Development (SCOReD 2009),2009:339-352.
[8] 苏建徽,余世杰,赵为,等.硅太阳电池工程用数学模型[J].太阳能学报,2001,22(4):409-412.