PWM整流器的无网压传感器DPC研究

卜文绍，翟利利，汪显博，袁澜

（河南科技大学 电子信息工程学院，河南 洛阳471003）

1 引言

随着功率电子技术和控制理论的发展，PWM整流器及其控制技术在高性能变频器、光伏并网逆变器、电力有源滤波器等方面的应用研究日益得到重视[1-11]。 针对PWM 整流器，已有不少控制策略[3，5，8-15]，其中直接 功率控制（DPC）策略因其较高功率因数、 简洁的控制算法和系统结构，得到了国内外的关注[3，7，8，12，14，15]。 从能量的角度看，DPC 就是在交流电压一定的情况下，将PWM 整流器的瞬时有功和无功功率控制在允许的范围内，从而间接把瞬时电流控制在允许范围内。 它采用直流电压外环、功率控制内环的双闭环控制系统结构。

基于电压定向的DPC 有电网电压传感器和无电网电压传感器2 种方案[5，8，12]。 其中有电网电压传感器的电压定向DPC 策略及其控制系统结构相对简单，但仍存在以下缺点：开关频率高且不稳定；直流侧电压、有功和无功功率波动较大；较多的传感器增加了控制系统的体积和成本。

传统的无网电压传感器技术，其瞬时功率是根据交流侧电流、 直流侧电压和PWM 整流器三相桥臂各功率器件的开关函数进行实时估算的[1，9，10]，是一种开环估算法。 这种估算与控制策略具有采样频率较高，瞬时功率估算依赖于当前开关状态，且开关频率也不固定；其最大的缺点是估算公式中含有导数项，从而影响了计算的准确性；进线电感L 也会对P 和Q 的估算精度产生影响。

有学者提出把虚拟磁链的概念引入到无网压传感器直接功率控制[6-7，14]，以解决基于电压定向无网压传感器直接功率控制系统的缺点，但仍未解决开关频率高、开关频率不固定的难点。

本文将在现有技术基础上，进一步研究基于虚拟磁链的电网电压闭环实时估算方法，并采用SVPWM 调制模块来代替传统开关表和滞环比较器，以期在恒频的基础上，更好地实现三相PWM整流器的无电网电压传感器DPC 控制。

2 基于电压定向的直接功率控制

2.1 三相电压型PWM 整流器结构和数学模型

图1所示为三相电压型PWM 整流器拓扑结构。其中：ua，ub，uc为三相对称电网电压，ia，ib，ic为三相进线电流；uao，ubo，uco为PWM 整流器交流侧相对于下桥臂节点O 的电压；udc为直流侧电压；edc为直流侧电势源；R 为功率器件与交流进线电感等值电阻之和，L 为进线电感，C 为直流侧电容，RL为负载电阻；uon为下桥臂节点O 与电源中性点N 之间的电压。

图1 三相电压型PWM 整流器的拓扑结构Fig.1 Topology of three-phase voltage source PWM rectifier

根据PWM 整流器的工作原理：当edc=0 或者edc＜udc时，三相电压型PWM 整流工作于整流模式；当edc＞udc时，工作于有源馈能逆变模式。

为建立三相电压型PWM 整流器的数学模型，做如下假设：

1）电网电压为三相对称正弦电压；

2）滤波电感是线性的，不考虑其饱和问题；

3）开关管为理想开关，无开关延时，无损耗。

定义：sa，sb，sc为三相桥臂功率开关器件的单极性二值逻辑开关函数，即

根据基尔霍夫电压定律，建立三相电压型PWM 整流器的基本方程为

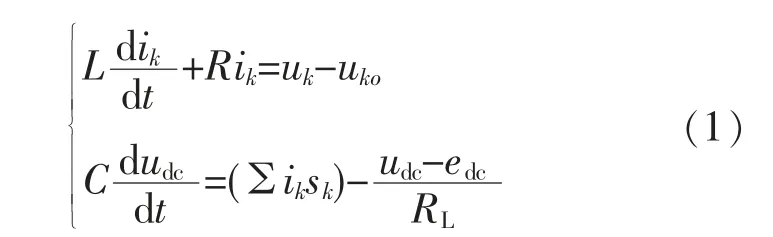
其中，uko为三相电压型PWM 整流器的交流侧电压，可表示为

在平衡三相电网电压的条件下，有：

将式（3）带入式（2），可得：

由此可计算出交流侧电压：

忽略R 的影响，把式（5）代入式（1），得：

再通过3/2 坐标变换，可得到静止αβ 坐标系下的电压分量为

同理，αβ 坐标系下的进线电流分量为

2.2 有网压传感器时的电压定向直接功率控制

图2为有电网电压传感器时的电压定向直接功率控制系统结构图。 它根据检测到的电压ua，ub，uc和电流ia，ib，ic来估算瞬时有功功率P 和无功功率Q；uα和uβ由ua，ub，uc经3/2 变换得到的，然后把uα和uβ送入扇区划分器可得到相应的扇区信号θn（θn=arctan（uα/uβ））； P 与Pref的差值、Q 与Qref的差值送入滞环比较器后得到二值开关信号SP和SQ。 Pref由直流电压外环PI 调节器的输出与直流电压相乘得到，若实现单位功率因数，Qref取为零。

图2 有网压传感器的电压定向直接功率控制系统Fig.2 DPC control system with power grid voltage sensor

该控制系统结构简单，数学模型易于实现；具有单位功率因数和低谐含量少等优点。 但较多的传感器使得系统装置体积大、成本高，且因传感器易受噪声干扰而降低系统性能；而且该系统的开关频率较高且不稳定，直流侧电压、有功和无功功率的波动较大，所以需要较大的滤波电感和采样频率。

2.3 无网压传感器时的电压定向直接功率控制

图3所示为无网压传感器时的电压定向直接功率控制系统结构，其工作原理与有网压传感器系统类似，不同之处在于无电网电压传感器的瞬时功率是根据网侧电流、 直流侧电压及功率器件的开关函数估算得到，省掉了电网电压传感器。

图3 无网压传感器电压定向直接功率控制系统Fig.3 None power grid voltage sensor DPC system based on voltage orientation

该系统虽然省略了网压传感器，但在功率估算中含有导数项，从而影响了估算精度。 这种估算方法实际上是一种开环估算方法，其自身不能根据相应的误差自行调节。 所以，要提高网压的估算精度和系统可靠性，有必要对更先进的电网电压估算方法进行深入的研究。

3 虚拟磁链定向的直接功率控制

3.1 基于虚拟磁链的瞬时功率估算方法

为了省掉电网电压传感器，基于电网等效磁链与电网电压之间的微分关系，采用类似交流电机磁链观测的方法来观测虚拟电网磁链。

根据电压的计算公式：

可得到电网磁链的计算公式为

再结合关系式：Ψ=Ψα+jΨβ和，得：

再根据有功和无功功率计算表达式：

式中：i*为i 的共轭矢量，i*=iα-jiβ。又可得到：

因为电网电压是三相正弦平衡对称电压，所以磁链的幅值是常数，即：

把式（14）带入式（13），即可得到瞬时有功与无功功率的解析算式为

所以，根据iα，iβ，udc和开关函数sa，sb，sc就可以实时估算出有功功率P 和无功功率Q。

3.2 基于虚拟磁链的无网压传感器DPC 系统

图4是传统的基于开关表的无电网电压传感器直接功率控制系统；图5是本文给出的基于虚拟磁链的SVPWM 无电网电压传感器DPC 系统结构。 两种直接功率控制系统结构、工作原理是类似的，最大的不同之处在于，为了稳定系统开关频率，在图5采用了SVPWM 调制模块代替图4中的开关表，采用双PI 调节器代替图4中的滞环比较器，解决了开关频率高且不固定的问题，从而可获得相对更稳定的直流侧电压，更低的电网电流畸变率和抗干扰能力。

图4 基于VFO 开关表的无电网电压传感器控制系统Fig.4 Power grid voltage senserless control system based on VFO switching table

图5 基于虚拟磁链的SVPWM 无电网电压传感器系统Fig.5 Power grid voltage sensorless SVPWM control system based on VFO

图5中，基于虚拟磁链的瞬时有功与无功功率估算值P和Q 与给定值P*和Q*比较后送入PI调节器，得到整流器交流侧dq 轴电压usd和usq，再经反旋转坐标变换，得到αβ 坐标系中的参考电压usα和usβ，即：

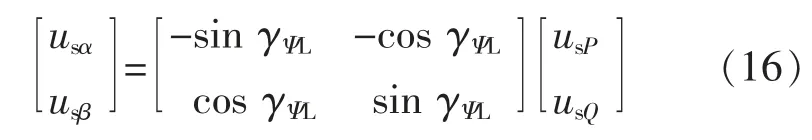
式中，γΨL为αβ 坐标系中的虚拟磁链向量角，可表示为

然后，利用SVPWM 调制，可得到PWM 开关信号Sa，Sb，Sc。

4 仿真试验与分析

根据图5所示的无电网电压传感器DPC 系统结构，搭建了系统仿真模型，并进行了系统仿真。

主要仿真参数为：电网电压Em=311 V，直流侧设定值600 V，网侧滤波电感5 mH，直流侧滤波电容4 700 μF。 图6～图9为系统的工作仿真波形。

从图6a 可看出，电压响应速度快，在0.03 s后就可以达到设定值600 V，并且电压波动很小；图6b 给出了整流器输入电压与电流之间的相位比较，除启动瞬间短时调整过程外，电流和电压始终同相位状态，实现了单位功率因数运行。

图7给出了给定电压突变时的工作波形。 当给定直流电压由600 V 突变为700 V 时，在双闭环控制系统的作用下，经过0.015 s 的短时调节，直流侧电压迅速达到并稳定在新的给定值700 V，如图7a 所示；在电压给定值突变的瞬间，交流侧相电流跟随直流侧电压的变化而变化，并与直流电压保持同相位。 波形对比表明了系统不仅具有快速的调节性能，还具有较高的控制精度，实现了可靠的单位功率因数控制。

图6 整流状态下的系统仿真波形Fig.6 Simulation waveforms under rectifying status

图7 整流状态下给定电压突变时的仿真波形Fig.7 Simulation waveforms when DC voltage is changed suddenly

图8给出了突加反电动势负载，实现能量回馈时的工作波形。 当在0.15 s 时突加反电动势时，系统经过短时调节后，快速转变到逆变运行状态，实现电流反相位和能量反流，即把负载能量顺利回馈到电网侧，还顺利消除了直流侧泵升电压。 从图8可见，在能量回馈过程中，相电流与相电压反相位，同样实现了单位功率因数稳定运行。

图8 从整流变为逆变状态时的相电压和相电流Fig.8 Voltage and current waveforms from rectifying waveforms to inverting

图9是有功功率P 与无功功率Q 的变化波形。 当直流侧电压稳定在600 V 时，无功功率始终为零，有功功率整流时稳定在4 kW，实现单位功率因数恒输出功率运行状态；在0.15 s 突加反电动势后，系统变为逆变运行状态，有功功率稳定在-4 kW，无功功率始终为零，实现了单位功率因数恒功率有源能量回馈。 图10给出了稳态运行状态下，电网虚拟磁链极坐标图。

图9 有功功率和无功功率波形Fig.9 Waveforms of active power and reactive power

图10 电网虚拟磁链极坐标图Fig.10 Polar chart of power grid virtual flux linkage

5 结论

首先介绍了三相电压型PWM 整流器的拓扑结构和数学模型； 然后给出了一种基于虚拟磁链的瞬时功率估算数学模型和方法，并用SVPWM调制模块代替传统的开关表，一则保证了开关频率固定，二则便于网侧滤波器的设计。采用连续PI调节器代替了传统的滞环调节器，获得了更加连续平滑的电流变化波形。 文中还给出了基于虚拟磁链和SVPWM 调制的无网压传感器DPC 控制系统结构，并对系统进行了仿真试验和验证分析。 通过网侧虚拟磁链实时估算电网电压，可省去电网电压传感器，也大大降低了控制系统成本。仿真试验结果表明：

1）采用所给控制策略和系统，不但可解决开关频率高且不固定的问题，而且还可获得更稳定的直流侧电压，更低的电网电流畸变率，且具有较高的抗干扰能力；

2）在给定直流侧电压突变的情况下，系统不但具有快速的调节性能，还具有较高的控制精度，实现了可靠的单位功率因数控制；过渡过程调节时间短，波形变化平稳；

3）在突加或提高反电动势负载的情况下，可快速实现电网电流的反相，快速进入能量回馈状态；无论在反电动势变化前或后，瞬时无功功率都约等于零，实现了单位功率因数运行控制。

仿真试验结果验证了所给估算方法、控制策略与控制系统的有效性和可行性。

[1] Daniel Wojciechowski.Grid Voltages Sensorless Control System of the PWM Rectifier with Active Filtering Function[C]∥Proc.of IEEE Compatibility in Power Electronics，2005:238－246.

[2] 赵焕，王红梅.基于虚拟磁链的PWM 整流器直接功率控制新调制策略[J].电力电子技术，2009，25（4）：41－44.

[3] 殷振环，梁晖.PWM 整流器直接功率控制研究[J].电力电子技术，2009，25（4）：41－44.

[4] Malinowski M，Jasin′ski M，Kazmierkowski M P.Simple Direct Power Controls of Three-phase PWM Rectifier Using Spacevector Modulation[J].IEEE Trans.on Industrial Electronics，2006，23（12）：6－19.

[5] 周永鹏，赵金程.三相电压型PWM 整流的新型直接功率控制[J].电气传动，2011，41（3）：38－40，45.

[6] 郑征，景小萍.虚拟磁链定向的PWM 整流器矢量控制研究[J].电气传动，2011，41（1）：38－41.

[7] 张颖超，赵争鸣，鲁挺.固定开关频率三电平PWM 三电平直接功率控制[J].电工技术学报，2008，23（6）：72－75.

[8] 唐雄民，朱燕飞.三相恒频PWM 整流器的直接功率控制研究[J].电气传动，2011，41（11）：32－37.

[9] Lee Dong-Choon，LimDae-Sik.AC Voltage and Current Sensorless Control of Three-phase PWM Rectifiers [J].IEEE Trans.on Power Electronics，2002，17（6）：883－890.

[10] Kwon Bong-Hwan，Youm Jang-Hyoun.A Line-voltage-sensorless Synchronous Rectifier[J].IEEE Trans.on Power Electronics，1999，14（5）：966－972.

[11] Toshihiko Noguchi，Hiroaki Tomiki.Direct Power Control of PWM Converter Without Power-source Voltage Sensors[J].IEEE Trans.on IA，2003，15（7）：115－122.

[12] 王久和，李华德，王立明.电压型PWM 整流器直接功率控制系统[J].中国电机工程学报，2006，26（18）：54－59.

[13] Nho N V,Youn M-J.Comprehensive Study on Space-vector-PWM and Carrier-based-PWM Correlation in Multilevel Invertors[J].IEEE Trans.on Electric Power Applications，2006，153 （1）：169-178.

[14] 赵仁德，贺益康.无电网电压传感器三相PWM 整理器虚拟电网磁链定向矢量控制研究[J].中国电机工程学报，2005，25（20）：56-61.

[15] 孙立琴，廖晓钟.PWM 整流器的定频直接功率控制[J].电气传动，2006，36（7）：39-42.