基于三电平的优化SPWM调制算法的研究

刘建坤，张伦健，李晓迅

（1.中国矿业大学 信息与电气工程学院，江苏 徐州221008；2.江苏省电力传动与自动控制工程中心，江苏 徐州221008）

1 引言

PWM 调制算法是三电平功率变换器控制系统的关键环节之一，其中基于零序分量注入的载波脉宽调制算法可以提高电压利用率，降低开关损耗等优化措施来达到空间矢量调制的效果，这两种调制算法之间存在着某种联系[1－4]，对于两电平和三电平逆变器，这种联系在本质上都是一致的。 因其结构的特殊性，三电平调制算法更加复杂。 对于三电平的研究中，三电平的零序分量是随小矢量的时间分配因子的变化而变化，零序分量表达都不尽相同，所以计算过程较为繁琐。本文研究由两电平零序分量注入法拓展到三电平，并分析两电平和三电平零序注入法的内在联系，推导出的三电平逆变器调制算法更加灵活，简单。

2 空间矢量调制与三角波调制的本质联系

常规的三角载波脉宽调制是一种相电压控制方式。 这种调制方法的最大调制度m 为1，线电压峰值最大为0.866Ud,相电压峰值最大为0.5Ud。 若在三相逆变器无中线系统中注入合适的零序分量，最大调制度就会提高m至1.154 7。 但是，不能简单的把零序分量作为3 次谐波[1]。对空间矢量调制和零序分量注入的三角载波脉宽调制关系分析如下 （以两电平为例）。

以第1 扇区为例，假设三角载波频率足够高，在一个载波周期内调制数值保持不变。 由图1得：

式中：，t7=kT0，T0=t0/(1-k)，T0为零矢量作用时间。以Ud/2 作为基准值进行标幺，由图1中相似三角形可得：

得到：

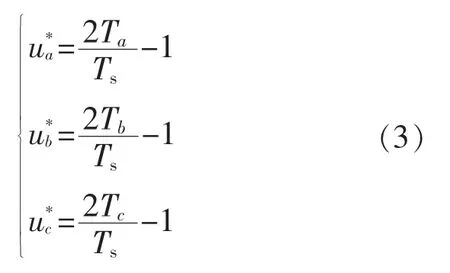
图1 SVPWM 各相比较时间(两电平)Fig.1 Compare time of each phase in SVPWM(two-level)

由式（1）、式（3）得到

带入式（3）、式（4）得到在扇区1 内零序分量表达式为

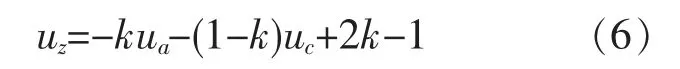
在1 个周期内零序分量表达式为

在两电平中，k 值表示零矢量分配时间的比例。 经过以上分析可知，在SPWM 的正弦调制波中加入式（7）所示的零序分量，可以得到和SVPWM 相同的调制波形。 说明了SVPWM 和SPWM的本质联系，SVPWM 是在SPWM 调制波中注入零序分量后，规则采样的结果。

3 两电平脉宽调制到三电平脉宽调制的拓展

在三电平逆变器中进行三角载波脉宽调制，如图2所示。

图2 SVPWM 各相比较时间(三电平)Fig.2 Compare time of each phase in SVPWM(three-level)

在很多文献中已经论述了三电平逆变器三角载波脉宽调制与空间矢量调制之间的本质关系[3-5]。由其关系得到的零序电压分量随着扇区的不同而不同，因而零序电压分量计算方法繁琐。 本文提出一种优化算法，可以大大简化零序分量的计算。

在三电平脉宽调制中，双载波与调制波进行来驱动开关动作。 其本质为双载波与调制波比较得到作用时间tm，再根据双载波与调制波的大小比较来判断在时间tm内开关管的动作。 因此，可以将与调制波的比较转换到一个载波中进行比较，得到相同的作用时间tm，等效于两电平载波脉宽调制。

在一个周期内，总是有两相电压正负极性相同，另一相电压与其相反。 以Ud/2 作为基准值进行标幺，当电压为正时，减1/2；电压为负时，加1/2，如图3所示。

图3 转换图Fig.3 Transition diagram

根据式（4）推出得：

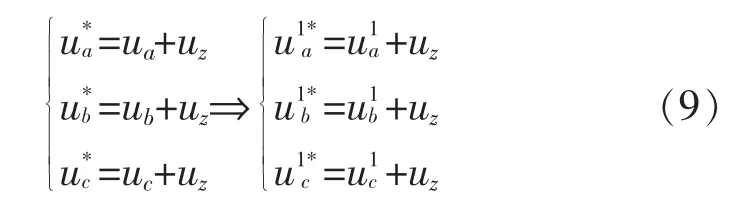
由式（2）～式（9）可得到零序分量为

由此可以看出，只需判断出在1 个载波周期内三相电压ua,b,c的正负极性，根据三相电压ua,b,c的正负极性对其进行修正，由式（10）就可以计算出三电平脉宽调制需要注入的零序分量。

4 两电平零序注入与三电平零序注入的内在联系

三电平空间矢量图如图4所示。

图4 三电平空间矢量图Fig.4 Three-level space vector diagram

式（1）中，t7=kT0，T0=t0/（1-k），T0为零矢量作用时间。 根据转换，在三电平控制中，T0为小矢量作用的时间，t0=（1-k）T0为首发小矢量作用时间，t7=kT0为后发小矢量作用时间。 通过控制正、负小矢量作用时间，即为控制比例k，就可以控制中点电位的平衡。k 值不同，得到的零序分量也不相同，改变注入的零序电压可以实现中点电位的控制。

5 实验验证

图5为调制比为0.6，0.8 和1.154 7 时，零序分量和注入零序分量后调制波的实验波形。

由图5可以看出，随着调制比的变换，零序分量和注入后调制波形也发生变化，直到m=2/时，调制比达到最大值。 和两电平的零序分量方式一致。

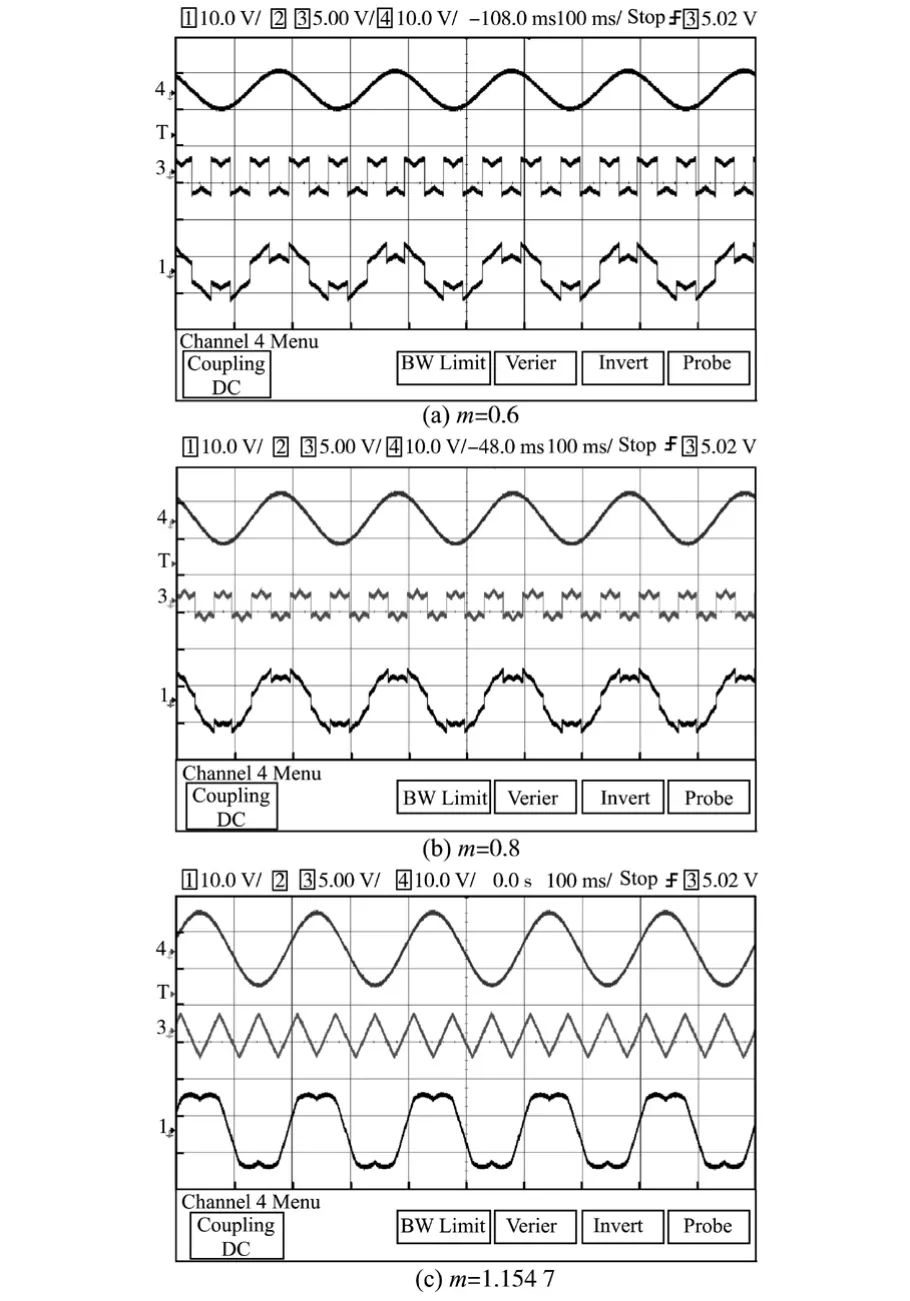
图5 三电平零序注入载波调制波形Fig.5 Three-level zero-sequence injected into the carrier modulation waveforms

图6～图8为使用该优化SPWM 控制策略进行三电平整流实验得到的线电压阶梯波、直流侧电压波形和相电压、电流波形。 电网电压峰值为75 V，直流母线电压设为180 V。

图6 线电压阶梯波Fig.6 Step wave form of line voltage

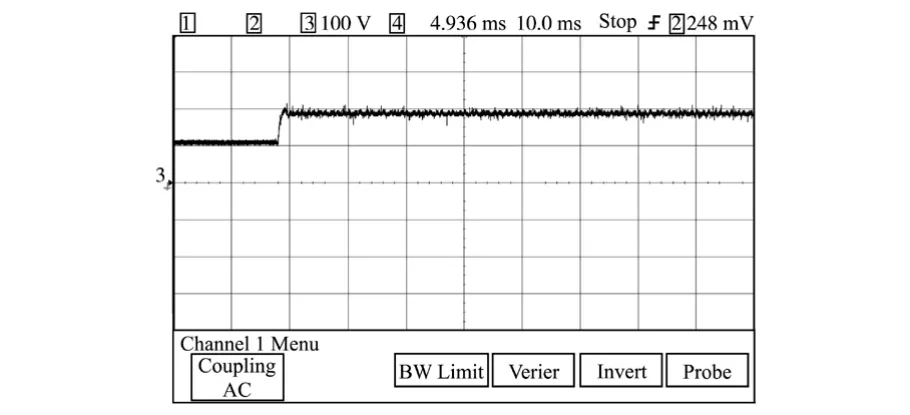
图7 直流侧电压波形Fig.7 Voltage waveform of DC side

图8 相电压和相电流Fig.8 Phase voltage and phase current

通过三电平整流实验验证了该优化SPWM控制策略的正确性。

6 结论

针对三电平逆变器在传统的零序注入SPWM 载波调制方法中，提出了一种优化的SPWM 算法。 研究了两电平与三电平在载波调制上的本质联系。 通过研究得出，三电平零序分量可以通过三相电压的修正后等效为两电平零序分量注入法计算得出。 大大简化了传统调制方法的繁琐。 该研究的方法也可应用于多电平载波PWM 控制技术中。

[1] 熊健，康勇，张凯，等.电压空间矢量调制与常规SPWM 的比较研究[J].电力电子技术，1999，2（1）：25-28.

[2] 李浩.大功率三电平变换器关键技术及同步电机传动控制系统研究[D].徐州：中国矿业大学,2008.

[3] 肖鹏，宋文祥，陈国呈.三电平空间矢量调制与三角载波调制内在联系的研究[J].电气传动自动化，2007,29（3）:7-10.

[4] 景巍.大功率三电平变频器功率器件损耗研究[D].徐州：中国矿业大学,2011.

[5] 宋文祥，陈国呈，丁肖宇，等.基于两类脉宽调制方式本质联系的三电平逆变器中点电位平衡控制的研究[J].电工技术学报，2005，20（12）：53-58.

[6] Jae Hyeong Seo.A New Simplified Space-vector PWM Method for Three-level Inverters [J].IEEE Transactions on Power Electronics, 2001,16（4）:545-550.