利用改进的遗传算法优化产品性能参数模型

梅小华 郑力新

(华侨大学信息科学与工程学院，福建 厦门 361021)

0 引言

标志工业产品性能的参数主要取决于零件的定值与容差。进行零件参数的设计，就是要确定其标定值和容差。将零件组装成产品时，若产品参数偏离预先设定的目标值，就会造成质量损失，偏离越大，损失越大;零件的容差大小则决定了制造成本，容差设计得越小，成本越高。正确有效地设计零件的最优化参数，是保证产品质量、减少产品总费用的重要环节。

零件参数优化设计的常用方法有梯度法、单纯形法和随机寻优法等。梯度法只能对连续参数进行运算，参数数量也不能太多，且容易陷于局部最优解。单纯形法受初值和计算步长的影响较大，易收敛于局部最优解。传统的随机寻优技术效率较低。遗传算法［1－2］是一种全新的优化搜索算法，它不受结构模型、约束条件和参数初值的限制，以其并行性和快速寻优等特点，解决了许多领域的难题，从而得到各界的重视。

基于上述认识，本文提出了一种改进的遗传算法，用来优化零件参数。该算法具有如下特点:①可变的交叉概率和变异概率使得寻优效率大大提高，改善了收敛性;②有效地消除了对参数初值的依赖性，不会陷入局部极值点;③具有较强的鲁棒性，是较好的大规模参数寻优方法。

1 零件参数的模型

1.1 问题提出

粒子分离器某参数(记作y)由7个零件的参数(记作 x1，x2，…，x7)决定，经验公式为［3］:

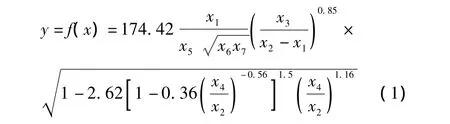
y的目标值(记作y0)为1.50。当y偏离目标值±0.1时，产品为次产品，质量损失为1000元;当y偏离目标值±0.3时，产品为废品，损失为9000元。

零件参数的标定值有一定的容许变化范围，容差分为A、B、C三个等级，用与标定值的相对值表示。A级为±1%、B级为±5%、C级为±10%。7个零件参数标定值的容许范围及不同容差等级零件的成本如表1所示。

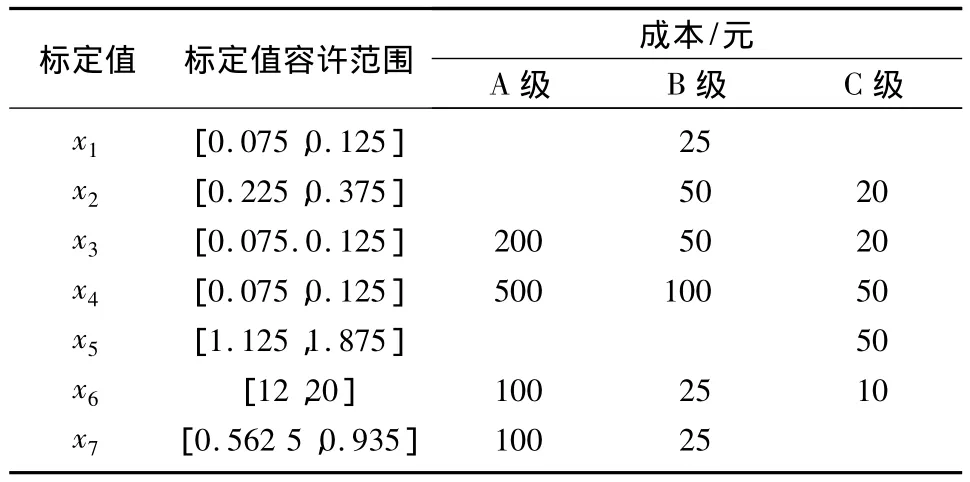
表1 零件参数标定值及容差等级Tab.1 Scaling values and tolerance levels of parts parameters

现进行成批生产，每批产量为1000个。在原设计中，7个零件参数的标定值为:x1=0.1、x2=0.3、x3=0.1、x4=0.1、x5=1.5、x6=16、x7=0.75;容差均取最便宜的等级。综合考虑y偏离y0造成的损失和零件成本，按照总经济损失最低的原则，进行零件参数(标定值和容差)设计。

1.2 基本假设

在设计零件参数时，作如下基本假设。

① 零件参数 x1，x2，…，xn为相互独立的随机变量，期望值和均方差分别记作xi0和σi，绝对容差记作ri=3σi，相对容差记作 ti=ri/xi0。

② 产品参数y由x1，…，xn决定，记作y=f(x1，…，xn)。由于xi偏离xi0很小，可在 x0=(x10，…，xn0)处对 f作泰勒级数展开，并略去二阶及以上项，有y=f(x0)+)，于是随机变量y的期望值为Ey=f(x0)，方差为或用ti表示为

③由y偏离目标值y0造成的(单件产品)质量损失记作L(y)，根据所给数据，可设L(y)与(y－y0)2成正比，即 L(y)=k(y － y0)2，可得 k=103/0.12=105。

④批量生产时，平均每件产品质量损失费EL(y)取决于零件参数标定值x0和容差t，记作:

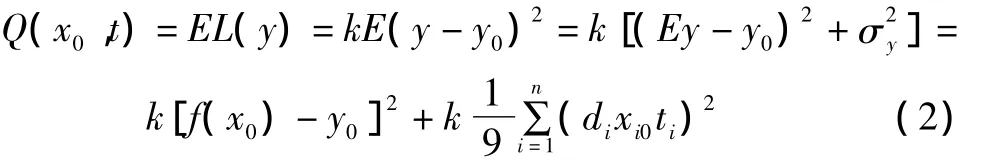
⑤单件产品的零件成本仅取决于容差等级ti，第i种零件的成本记作ci(ti)，于是零件总成本为C(t)=。

⑥综合考虑y偏离y0造成的损失和零件成本，将本问题的目标函数定义为成批生产时平均每件产品的总费用，即 z(x0，t)=Q(x0，t)+c(t)。

2 遗传算法

遗传算法首先随机地产生一组潜在的解X(该解称为“染色体”，解的特定集合称为“种群”，解中的变量称为“基因”);然后采用生物进化的过程(如染色体交叉、变异、淘汰等)，不断提高解的品质;最后获得最优解。

遗传算法不要求具有梯度信息，就可以处理大量的离散参数运算，因此非常适用于上述粒子分离器参数的设计。

2.1 编码策略

粒子分离器参数包括7个连续参数xi和7个离散参数ti，根据参数范围的限制，采用二进制进行编码，粒子分离器参数的二进制编码如表2所示。

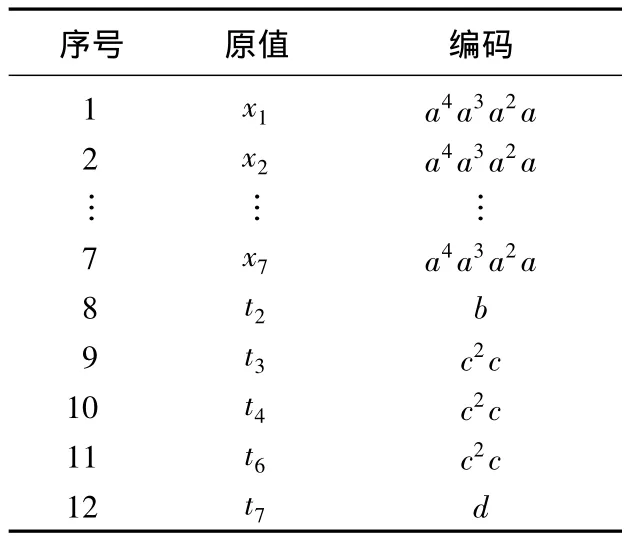
表2 参数二进制编码Tab.2 Binary coding of parameter

表2 中，a、b、c、d 取 0 或 1，xi编码长度为 4，t2、t7编码长度为 1，t3、t4、t6编码长度为 2，t1、t5不参加编码，因此染色体长度为36。在此情况下，采用二进制编码的精度已足够。若精度要求发生变化，编码的位数可根据实际的精度需要选取。

2.2 目标函数的建立

总费用的目标函数［4－5］为非线性规划模型，由零件成本费和产品参数偏离目标值y0引起的质量损失费组成。零件成本由简单的线性代数确定，质量损失是涉及概率分布的非线性函数。标定值或容差设计得不合理，会使产品参数远离目标值，造成质量损失;而容差设计得太小，又会增加零件制造成本。为了使总费用Z(x0，t)达到最小，且满足约束条件，即标定值x0落在给定的容许范围内，本算法所采用的目标函数为:

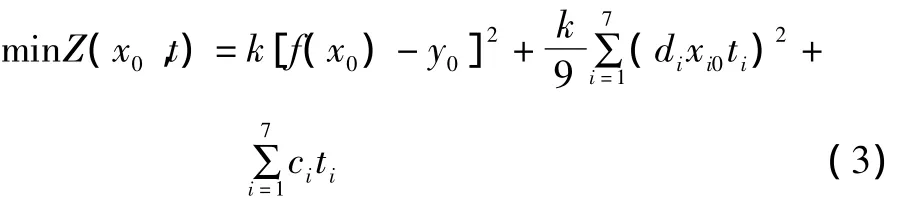
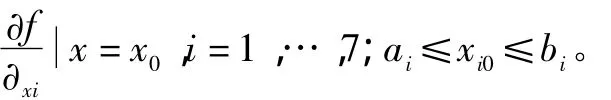
2.3 遗传算法与粒子分离器的结合

算法设计如下。

①全局变量设定，给出群体规模m、最大迭代次数 Tmax的大小，选择 m=100、Tmax=150，k为当前进化的次数。

②种群的产生及初始化。设进化代数计数器T=0，以零件参数为基因组成染色体X，X由36个基因组成。初始染色体中的基因(设计参数)在各自的取值范围内随机产生，但必须满足所有约束条件。种群由m个染色体构成。

③适应度函数值计算和选择操作。适应度函数是选择操作的依据，适应度函数应是非负的，假设适应度函数为:

式中:f(x)为模型目标值。

目标函值较小的个体对应的适应度较大，在选择操作中被选中的概率也较大。算法中采用适应度比例策略和保存最优策略相结合的方式［6］进行选择操作，每次只保留所有进化代中适应度最大的个体。选出m个优良个体的步骤如下。

根据适应度函数，计算每个个体的适应度Fi(i=1，2，…，m)，得到的每个个体的适应概率为:

根据每个个体的适应概率，得到每个个体的累积概率为:

随机产生一个(0，1)的实数r，对m个累积概率进行判断，若 Qi－1＜r＜ Qi成立，则第 i个个体便是被选中并留在基因池的个体;重复以上步骤，直到选中m个个体。

④交叉概率Pc与变异概率Pm的计算。其中一种方法是采用 Pan等人［7－8］提出的 Pc和 Pm能够随适应度自动改变的自适应遗传算法。当群体最大适应度fmax与平均适应度favg接近时，群体趋于收敛，即此时群体中的各个个体趋于一致，其父代间的距离比较小，群体的多样性较弱。为了提高群体的多样性，应增大Pm;反之，则群体多样性较强，应减小Pm。此方法对算法时间和空间复杂度要求较高，程序运行时间较长。另一种方法是采用Pc和Pm都随迭代次数的增加而逐级变化的遗传算法。该方法在进化的初期交叉率较大，变异概较小，可以防止群体的早熟。在进化后期，交叉率较小，变异率较大，寻优过程加速。但该方法要求最大迭代次数较大，若最大迭代次数较小，则每代Pc和Pm变化幅度较大，不利于在规定次数内保证算法的收敛性。

针对上述问题，本文将以上两种方法相结合，在算法中采用随迭代次数变化的变异概率和自适应变化的交叉概率。

交叉概率为:

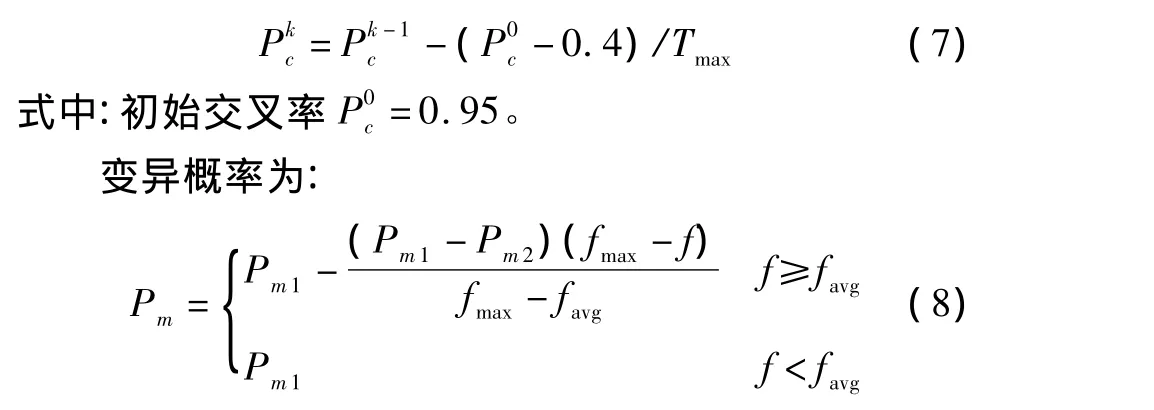
式中:f为变异个体的适应度;fmax为群体最大适应度;favg为平均适应度;Pm1=0.1、Pm2=0.001。

⑤交叉、变异操作。对父代群体进行两两配对，然后对每对个体按Pc概率进行交叉操作。采用多点交叉，在36个基因中的前28个基因中，随机产生一个交叉点;在后6个基因中也产生一交叉点，经过交叉运算后得到子代群体编码。对于子代群体编码的每一位，采用多点变异，以Pm的概率进行变异，生成新一代群体。

⑥过程结束判定。当最优个体的适应度和群体适应度不再上升时，算法的迭代过程收敛、算法结束;否则，用经过选择、交叉、变异所得到的新一代群体取代上一代群体，并返回到步骤③继续循环执行。

3 仿真结果

以零件参数设计为例，在CPU 2.0 GB、内存512 MB的机器上用 Matlab 6.0 对其进行仿真［9－10］，在遗传代数T=80时，得到如下结果。

单位产品总费用min z=748.9349元，与原设计费用z0=6507.2相比，费用减少了5758.3元，产品质量参数值 Ey=1.4976。

目标值进化曲线如图1所示，各种遗传算法目标值进化曲线如图2所示。

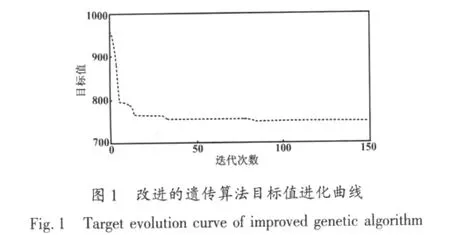
Jong D提出了两个评价遗传算法性能的指标，即在线性能指标和离线性能指标。根据图1仿真结果可知，在线性能指标为4.0568×104，说明算法具有很好的动态性能;离线性能指标为755.3421，说明算法具有很好的收敛性能。仿真运行表明，改进的遗传算法，其4/5的主程序(20次)的最小费用值落在(748～752)元之间，表明改进的遗传算法在解决大规模参数设计中具有较好的稳定性。

4 结束语

将改进的遗传算法应用于零件的参数寻优，寻优效率较简单遗传算法有了大幅提高;在保持群体多样性的同时，又保证了算法的收敛性，可为大规模参数设计提供捷径。

［1］Holland J.Adaptation in neural and artificial systems［M］.Ann Arbor:Michigan University，1975.

［2］张文修.遗传算法的数学基础［M］.2版.西安:西安交通大学出版社，2003:146－202.

［3］1997年全国大学生数学建模竞赛(A题)［J］.数学的认识与实践，1998(1):2－4.

［4］赵静.数学建模与数学实验［M］.北京:高等教育出版社，2000:64－73.

［5］吴新烨，徐学林.在零件的参数优化设计中的数学建模［J］.煤矿机械，2004(1):10 －12.

［6］Filho J L R，Treleaven P C，Alippi C.Genetic algorithm programming environments［J］.IEEE Computer，1994，27(6):28 －43.

［7］熊军，高敦堂，都思丹，等.变异率和种群数目自适应的遗传算法［J］.东南大学学报:自然科学版，2004(4):553 －556.

［8］Pan Zhengjun，Kang Lishan，Nie Sixiang.Evolving both the topology and weights of neural network［J］.Parallel Algorithms and Applications，1996，9(3):299 －307.

［9］王小平，曹立明.遗传算法－理论、应用与软件实现［M］.西安:西安交通大学出版社，2003:104－122.

［10］雷英杰.Matlab遗传算法工具箱及应用［M］.西安:西安电子科技大学出版社，2005:95－105.