一种关联回路的控制性能评价方法

李昕泽 李宏光

(北京化工大学信息科学与技术学院，北京 100029)

0 引言

近年来，控制回路之间的相关性对控制性能的影响受到广泛的关注;然而目前的多变量控制性能评价方法都不能在这个问题上给出令人满意的答案。

1996年，Harris等把单变量最小方差控制准则引入到多变量控制系统中，利用多变量谱因子分解和多变量丢番图方程的解来描述多变量控制系统的性能［1］。Huang等拓展了这一思想，提出了系统滤波和相关性分析算法，并通过把单变量回路中的时间延迟引申为关联矩阵，最终将该算法推广到多变量系统［2－5］。Isaksson和 Burch等提出了 PID 控制回路的性能评估和监测方法［6－7］。Ko＆ Edgar给出了以PID参数为自变量的闭环输出的直接表达式，采用迭代算法计算可达的最优PID控制回路性能及相应的最优PID参数［8］。Harris利用方差分析的思想，在分析前馈-反馈系统内各部分扰动的作用后，形成了一个总方差［9］。这种对前馈-反馈控制系统中各部分扰动作用进行分析的思路也是本文主要分析思想的来源。

1 关联回路控制性能分析

关联控制系统框图如图1所示。

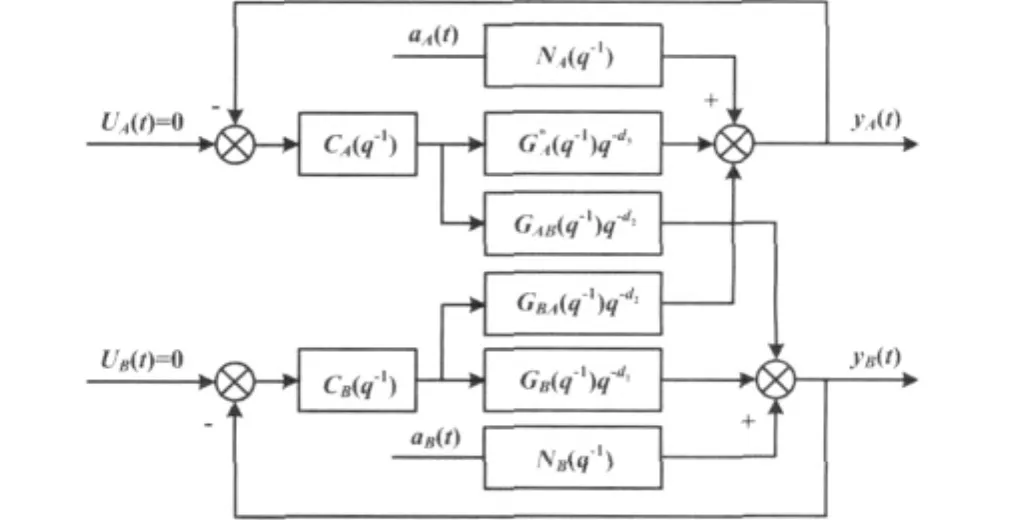
图1 关联控制系统框图Fig.1 Block diagram of the correlated control system

图1中，GA和GB分别为被控对象模型;GAB和GBA为两个回路之间的关联模型;CA和CB分别为两个回路的PID控制器模型;NA和NB分别为两个回路的噪声模型;aA和aB分别为施加在A、B两回路的噪声。

若两个控制回路的设定值均不发生变化，则有:

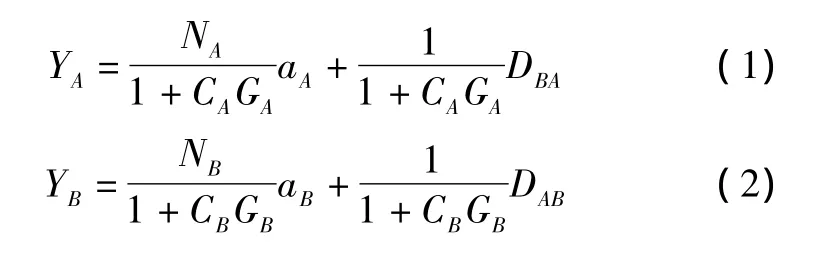
最终得到输出的离散平移形式为:

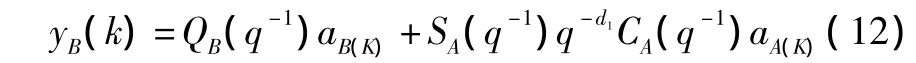
式中:QB(q－1)aB(K)为自身回路的输出方差，主要与aB有关;而 SA(q－1)q－d1CA(q－1)aA(K)不仅与 aA有关，而且还与A回路的控制器CA有关。同理可获得A回路输出的离散平移形式，即:

由此可见，控制器不但会对主回路的性能造成影响，同时也会影响关联控制回路的方差。造成这种现象的主要原因是最小方差控制的目标是首先保证主回路中存在的方差最小，这也是控制器设计的初衷。而如果将关联模型看作是控制器的另一个控制对象，就不能保证在关联通道中存在的方差为最小。

2 关联系统评价方法

利用PID可达最小方差算法，将关联回路信息加入式(12)，利用分别求取两部分方差;并利用两部分方差之和来代表回路总方差，作为耦合回路控制性能的评价基准，从而达到分解耦合回路中方差的目的。

对于图1的关联控制回路，以B回路为评价回路，系统的脉冲响应可以表示为:

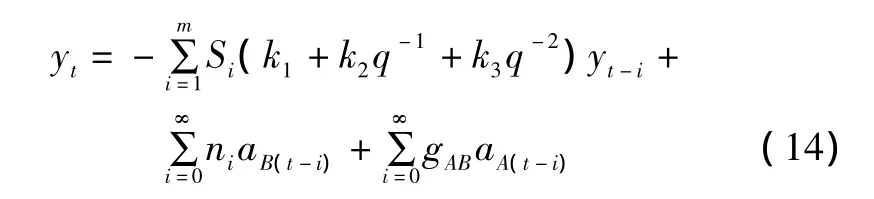
式中:Si等价于过程模型的阶跃响应系数;ni为噪声的脉冲响应系数;gAB为扰动脉冲响应系数;m为系统达到稳态时刻的采样次数。

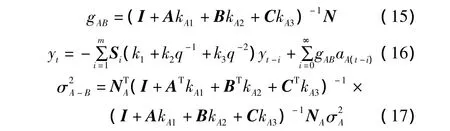
式中:k1、k2、k3为B回路的控制器PID参数;N为噪声的脉冲响应系数;gAB为扰动脉冲响应系数。对σ2PID进行优化

求解，可以获得能够使得回路方差最小的PID参数k1、k2、k3，优化求解步骤如下。

④优化求解

优化求解是指利用线性逼近求取非线性方程组的极值，令 k=［k1k2k3］T，则有:

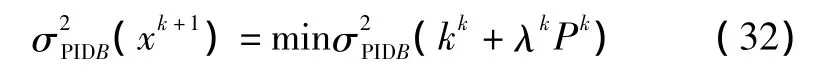
式中:kk、Pk分别为第k次迭代的k和P的取值;λ为搜索步长，λ∈(0，1)。

本文利用牛顿迭代法，采用一维寻优搜索对PID的输出方差进行寻优。使用0.618法，在Pk方向搜索最优的kk，使 σ2PIDB(xk+1)最小。λk∈(0，1)，区间原长为1，每次迭代缩短区间的比例为0.618。通过迭代计算，最终可以得到过程的最小输出方差以及最优PID控制器参数。

3 实例研究

两输入两输出系统的各部分模型分别为:

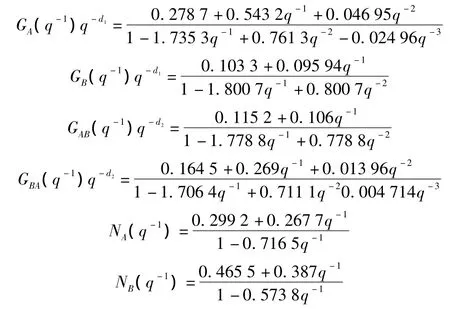
A、B两个控制回路均采用PI控制，A回路控制器初值为k1=3、k2= －1，B回路控制器初值为 k1=4.5、k2=－1.5，获得B回路控制性能评价的相关数据如表1所示。

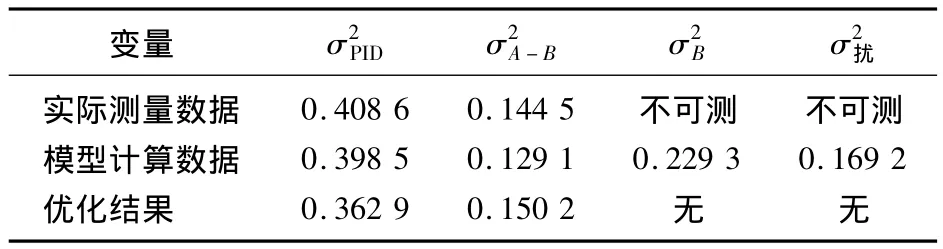
表1 控制性能评价数据Tab.1 Assessment data of control performance

由表1可以看出，基于本方法计算得到的数据与实际测量数据基本一致，最终获得B控制回路的控制性能评价指标为:

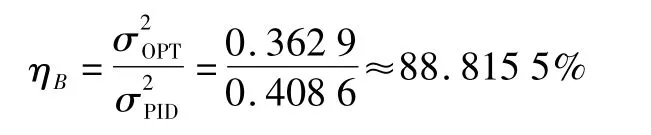
同时，可以计算A、B两控制回路之间的扰动评价指标为:

这个指标表明了B回路的控制性能受A回路的影响程度，且可以利用ηAB辅助ηB评价控制回路的性能。即当ηB发生变化而ηAB的变化不大时，说明B回路本身出现了性能问题;而当两者均发生明显变化时，则说明A回路出现性能问题的可能性较大。

当整定一个回路的PID参数时，既要考虑自身回路的性能，同时也要兼顾其对关联回路的影响。如何获得一个折中点还有待进一步的研究。

4 结束语

通过对关联回路内部扰动进行分析，操作人员可以在多个控制回路性能同时出现问题时，尽快地找出原因。目前的方法还主要依赖于完整的控制对象状态空间模型，下一步的研究重点在于如何简化求取各部分方差。同时，由于控制回路之间的扰动实际很难识别，应该寻找一种能够表征回路之间实际扰动的方法。

［1］Harris T J，Boudrean F，MacGregor J F.Performance assessment of multivariable feedback controllers［J］.Automatica，1996，32(11):1505－1518.

［2］Huang B，Shah S L，Kwok E K.Good，bad or optimal?Performance assessment of multivariable processes［J］.Automatica，1997，33(6):1175，1183.

［3］Huang B，Shah S L.Practical issues in multivariable feedback control performance assessment［J］.Journal of Process Control，1998，8(5):421－430.

［4］Huang B，Ding S X，Thornhill N F.Practical solutions to multivariate feedback control performance assessment problem:reduced a priori knowledge of interactor matrices［J］.Journal of Process Control，2005，15(5):573 －583.

［5］Huang B，Ding S X，Thornhill N F.Alternative solutions to multivariate control performance assessment problems［J］.Journal of Process Control，2006，16(5):457 －471.

［6］Isaksson A J.PID controller performance assessment［C］//Proceeding Control Systems Conference，1996.

［7］Burch R.Monitoring and optimizing PID loop performance［C］//ISA Annual Meeting，2004.

［8］Ko B S，Edgar T F.Assessment of achievable PI control performance for linear processes with dead time［C］//Proceecding American Control Conference，1998.

［9］Huang B，Shah S L，Miller R.Feed forward plus feedback controller performance assessment of MIMO systems［J］.IEEE Transactions on Control Systems Technology，2000，8(3):580 －587.