数据采集器采样速率评价方法研究

岳瑞华 徐中英 杨学猛

(第二炮兵工程大学自动控制工程系，陕西 西安 710025)

0 引言

数据采集器的采样速率是指采集通道在单位时间内所采集的数据个数，通道间延迟时间是指在不同通道间切换时所需时间。

数据采集器得到的是离散化数据，通过对离散化数据的处理可得到需要的测量结果。数据采集器的采样速率和通道间延迟时间［1－2］直接决定离散数据和时域的关系。因此，对数据采集器的采样速率和通道间延迟时间的评价是正确选择和使用数据采集器的基本条件。

1 采样速率的评价方法

一般评价系统使用标准周期计数法对采样速率进行评价［3－4］，但某些测量系统中配置的是标准信号源，如标准信号源Fluke5520A，标准信号源能够提供标准正弦信号。因此，本文采用标准正弦波信号和自相关方法评价数据采集器的采样速率。其基本思想为:标准信号源送出标准正弦信号，频率为f=100 Hz;标准频率信号1 年绝对不确定度为(2.5 ±5)×10－6Hz［5－6］，启动数据采集器采集N个数据。利用自相关技术［7－10］消除采集数据中的噪声和干扰，然后，寻找出N个数据中所包含的输入信号整周期的个数nc和nc个整周期所包含的采集数据个数Nc，则采样速率fs为:

式中:nc为输入信号整周期的个数;Nc为nc个整周期所包含的采集数据个数;f为标准信号的频率，Hz;KT为在一个信号周期中包含的采样个数，也称为信号的数字化周期。

由于标准信号的频率f已知，由式(1)可知，评价工作的重点是KT的获取。

式(1)与一般的标准周期计数法的计算公式相同，本文不再赘述。不同的是，一般的标准周期计数法直接对应采集数据，式(1)却对应采集数据的自相关离散序列，原因如下。

原始的采集数据不可避免地包含噪声和干扰，在自相关处理后，可以有效地抑制噪声和干扰而不改变数据序列的周期。判断自相关后的数据序列的可信度比直接判断采集数据序列高。自相关分析原理如下。

所谓自相关，就是信号与自身进行相关运算得到其自相关函数，信号的自相关函数具有保持信号周期不变的特性。为了说明这一点，假设信号x(t)具有周期T，即:x(t)=x(t+nT)。x(t)的傅里叶级数表达式为:

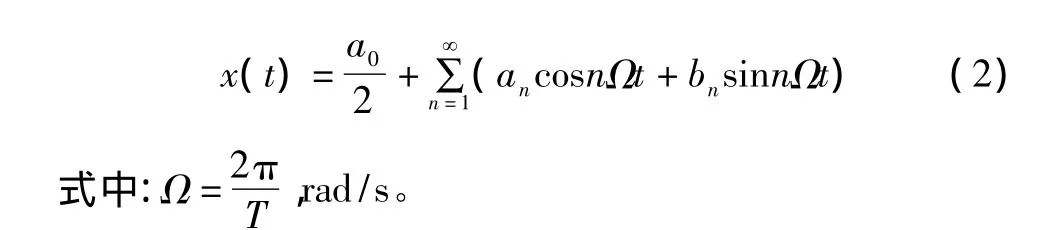
这时信号x(t)的自相关函数Rxx(t)可用傅里叶级数表示为:

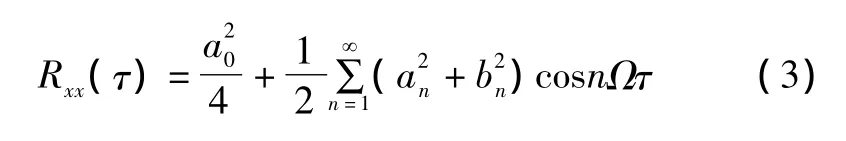
由式(3)可知，周期信号的自相关函数也是同一基频的周期函数。Rxx(τ)包含x(t)的全部频率分量，各频率的振幅等于相应的傅里叶系数的均方值，振幅变化依赖于振幅本身，且是非线性变化。但x(t)中不同频率分量的相位在Rxx(τ)中归零，采用过零点判断信号数字化周期时，只关心过零点时数据符号的变化。因此，Rxx(τ)中不同频率分量的相位归零对于采用过零点判断信号数字化周期是非常有利的。

在一般情况下，信号不仅由基波及其谐波组成，还不可避免地包含噪声和干扰，在数字化过程中，还要加入量化噪声等。因此，一般可假定记录x(t)是由周期信号s(t)和随机噪声n(t)组成，即:x(t)=s(t)+n(t)。噪声n(t)的均值为零，与s(t)不相关。x(t)的自相关函数为:

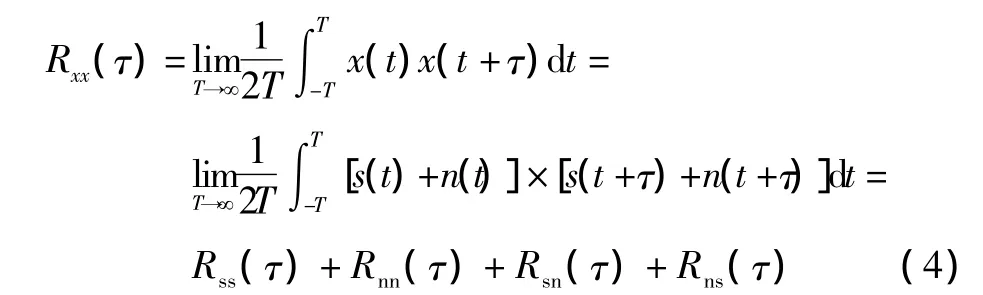
式中:Rss(τ)为周期信号的自相关函数;Rnn(τ)为噪声信号的自相关函数;Rsn(τ)为噪声信号与周期信号的互相关函数;Rns(τ)为周期信号与噪声信号的互相关函数。

由式(4)可知，由于s(t)和n(t)不相关，式(4)中的后两项即Rsn(τ)+Rns(τ)等于0。n(t)为非周期的噪声，所以Rnn(τ)随τ的增大而减小。因而当τ=τ1时，有:

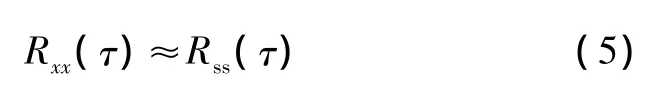
当 τ＞ τ1时，可用 Rxx(τ)近似地表示 Rss(τ)。所以当τ足够大时，Rxx(τ)所表现出的周期性就是x(t)中所包含的周期信号s(t)的周期。

采用自相关理论处理数字化数据，得到的自相关序列保持了原数据的周期，且抑制了噪声对数据的污染。由于实际测量数据中谐波和干扰幅度一般小于有用周期信号幅度，自相关运算的振幅响应是非线性函数，即:原振幅为A，则自相关函数振幅为，振幅改变量为倍。相对而言，自相关运算加强了有用周期信号的幅度，换言之，其抑制了谐波和干扰的作用，对于信号周期确定的准确性十分有利。

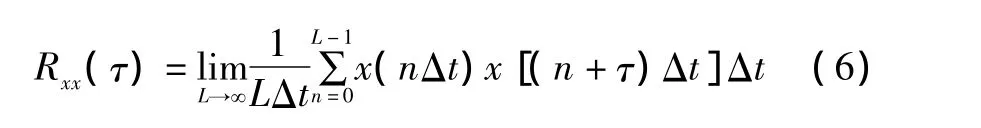
式中:x(nΔt)为第n个数采值，简记为x(n)。

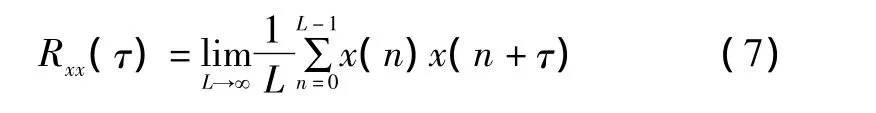
由于数采点为有限值，L不可能为无穷，由相关理论分析可知，信号中包含的噪声是随机的，具有独立性，且与周期性信号不相关，所以假定在一个完整周期内进行自相关，Rsn(τ)和 Rsn(τ)也可视为0，Rnn(τ)也得到了充分抑制。根据信号的周期性可知，在一个周期内的自相关与在若干个(包括无穷)周期内的自相关是一样的。考虑到经自相关运算后得到的自相关序列应至少体现一个完整周期，所以L的长度至少应包括两个完整的信号周期。由于自相关后的相位归零，为保证自相关序列中至少有两个同方向过零点，L的长度应扩大到包含3个信号周期。

2 运算长度的周期性影响

在一般情况下，本文提出的采样速率评价法只能估计信号的周期而无法准确预知，即自相关运算的长度L无法保证恰好是信号周期的整数倍。同时，为便于说明运算长度对自相关序列的周期性影响，假设信号为 x(t)=sinΩt，积分时间为 T'，则:

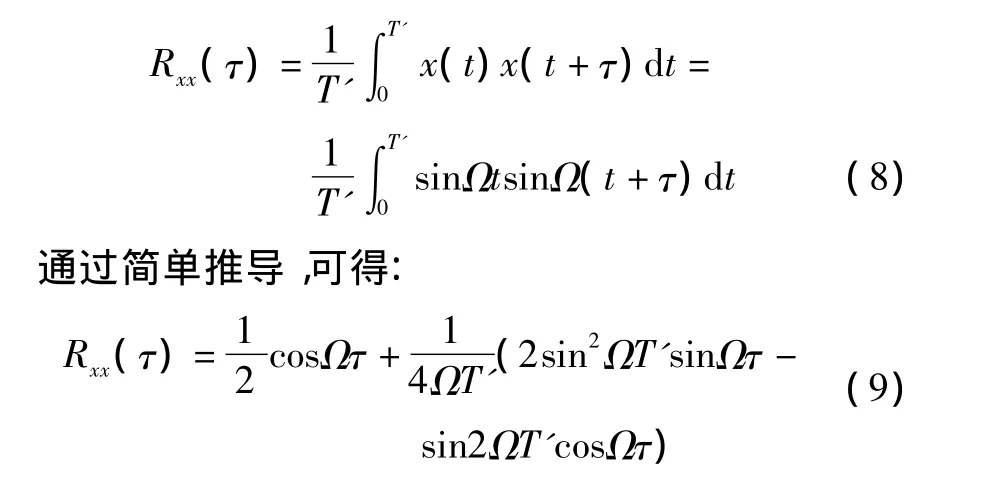
式中:等号右侧的第2项幅度可近似地认为与ΩT'成反比。当采样周期足够长时，非整数周期的影响可以忽略不计，则与数采长度 T'无关。实际应用中，ΩT'＞6π，即大于3个周期即可。一般情况下，数采长度取信号周期上限的5～10倍并不困难。

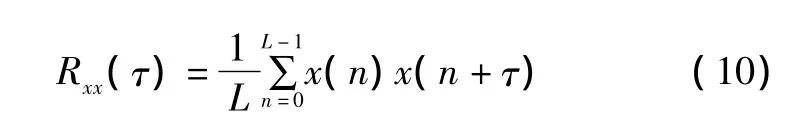
式(10)即为最终的自相关序列计算公式。通过对Rxx(τ)的逻辑判断(过零点判断)，可以方便地得到KT，进而求得数据采集器的采样速率。

3 仿真试验及结论

下面对自相关方法求取KT进行简单的仿真试验，以验证上述论证。

利用计算机产生x(n)数据采集序列，对这些序列进行自相关运算，得到的结果如下。

①非整周期运算对结果的影响

当x(n)=sin(8π/1024n)时，相当于每周期包括256个数据采集点，采样长度为1024，自相关运算长度分别取 1024、924、824、724，得到的自相关序列采用过零点判断，数字化周期均为256。

由以上分析可知，非整周期运算对数字化周期的影响可以忽略。

②噪声对运算结果的影响

当x(n)=sin(8π/1024n)+rand(－0.5，+0.5)时，(rand()表示服从均匀分布的随机数)，原始数据根本无法采用过零点判断数字化周期。采用自相关运算后，当运算长度为1024、924、824时，数字化周期为256;当运算长度为724时，数字化周期为254或255或256。由以上分析可知，随着运算长度的减小，抑制噪声能力有所下降，因此，应保证足够的运算长度。

③谐波(干扰)对运算结果的影响

当自相关运算长度分别为1024、924、824、724时，数字化周期分别为257、256、255、255。由以上分析可知，自相关算法具有足够的抗干扰能力。

将激励信号加载到单通道和双通道后，分别得到采样时间(采样速率的倒数)。单通道测量时采样速率快，即采样时间短;双通道测量时采样速率慢，其原因是通道转换需要一定时间。因此，两者之差即为通道间延迟时间。

4 结束语

本文为有效抑制采样速率评价过程中采样数据受噪声和干扰的影响，提出了一种采用标准信号源提供标准正弦信号和采用自相关滤波技术对采样速率进行评价的方法。

该方法能够有效地抑制采样数据受噪声和干扰的影响，方法简单、计算量小，评价数据的一致性好，仿真验证了该方法的有效性。在某测试设备计量检定系统中，该方法利用评价得出的采样速率和数字化周期进行交流电压测量和相位测量，满足了计量检定系统的要求。

［1］赵冬青，任勇峰.高速数字采集系统通道间信号传输延迟时间分析［J］.测试技术学报，2011，25(2):178 －182.

［2］梁志国，朱济杰.数据采集系统通道间延迟时间差的精确评价［J］.仪器仪表学报，1999，20(6):619 －623.

［3］梁志国，孙璟宇.采集速率评价结果的不确定度［J］.华北工学院测试技术学报，2000，14(1):35 －38.

［4］国家技术监督局 JJG 1048-95.数据采集系统校准规范［S］.1995.

［5］中国人民解放军总装备部 GB 3756-99.测量不确定度的表示及评定［S］.1999.

［6］李金海.误差理论与测量不确定度评定［M］.北京:中国计量出版社，2003.

［7］杨德钊，宋凝芳，林志立，等.基于相关及相位差法的高精度频率估计算法［J］.北京航空航天大学学报:自然科学版，2011，37(8):1030－1033.

［8］岳瑞华，许化龙.数采信号周期确定自相关方法研究［J］.电子测量与仪器学报，2002，16(Z):1248 －1251.

［9］岳瑞华，许化龙，刘根旺.基于相关分析的交流电压测量［J］.航空计测技术，2004，24(1):17 －18.

［10］郭永彩，廉飞宇，林晓钢.数字信号处理［M］.重庆:重庆大学出版社，2009.