簇类特征城市群间的TSP问题研究

王 兴

(武汉科技大学信息科学与工程学院，湖北 武汉 430081)

0 引言

旅行商问题(traveling salesman problem，TSP)是指寻求N个城市间遍历所有城市的最短路径。该问题是一个经典的组合优化问题，所有的路线组合数为(N-1)!/2。当遍历的城市数不断增加，其搜索空间随着城市数N的增大而迅速增大，并且遍历所有城市所需时间为问题规模的指数阶时间。针对该问题已经提出了多种有效算法，如最近邻居法、贪婪算法、集群算法等［1－2］。由于群体规模较大，需要对较多的个体进行大量的遗传和演化操作，从而使得演化运算过程进展缓慢，难以达到相应的计算速度要求。

现实生活中，许多城市在地域上的分布经常呈现区域特征，所以在寻求最优路径时，应首先提取城市的遍布特征，以相应地减少全局搜索最优解的盲目性;然后再配合使用一些优化算法的组合，从而大量节省最优解的寻解时间。

本文基于上述思想，提出了一种基于平衡聚类的TSP演化算法。

1 聚类算法

根据同类数据集应具有相近特性，而不同数据集在这些特性上差异较大的假定，将所研究的数据集进行分类，这种研究方法称为聚类［3－4］。聚类是数据挖掘、模式识别等研究方向的重要研究内容之一，传统的聚类算法在识别数据的内在结构方面往往指导性不强，从而导致聚类算法效率过低。本文为了加强聚类的收敛速度，在使用传统的聚类算法前，采用城市群稀疏度初提取的方法为以后的聚类提供相应指导。

1.1 城市群稀疏度的提取

随着当今卫星航拍技术的发展，可以很轻易地得到分布在各个地区的货物配送城市的地图。这些地图是提取城市群稀疏度最后的依据。城市群稀疏度提取的步骤具体如下。

首先将这些货物配送城市的地理位置量化成具有二维属性的数据空间S=S1×S2。将每维空间均匀地划分为p份，则共有p×p个单元网格。所有代表城市的二维地理分布特征数据点将遍布在这p×p个单元网格中。

然后计算每一个单元网格的城市分布稀疏度ρ=nij/N(其中nij为第i行j列的单元网格，N为总城市数量)。与此同时，确定网格密度的阈值，网格单元的密度阈值参数在很大程度上影响算法的聚类质量。在此选取平均密度作为阈值，具体平均密度求解为:

式中:ρij为非空网格密度;M为非空单元网格数。

最后，判别每一非空单元网格的稀疏性。当某一单元网格的密度时，则判定该单元网格为过稀疏网格;当时，则判定该单元网格为稀疏网格;当时，则判定该单元网格为密集网格;当时，则判定该单元网格为过密网格。

1.2 K-均值聚类

K-均值算法是一种得到广泛使用的聚类算法［4］。它是将各个聚类子集内的所有数据样本的均值作为该聚类的代表点。算法的主要思想是通过迭代过程，将数据集划分为不同的类别，使评价聚类性能的准则函数达到最优，从而使生成的每个聚类类内紧凑，类间独立。

K-均值算法描述如下。

①为每个聚类确定一个初始聚类中心，这样就有K个初始聚类中心。

②将样本集中的样本按照最小距离原则分配到最邻近聚类。

③将每个聚类中的样本均值作为新的聚类中心。

④重复步骤②～步骤③，直到聚类中心不再变化。

⑤结束，得到K个聚类。

1.3 平衡聚类算法

根据K-均值聚类的算法原理可知，一旦当聚类的样本点过多，算法的迭代次数就迅速增加。因此，可以通过提前学习，提取样本分布特征来指导K-均值聚类，使其成为一种有监督的聚类算法。在此提出平衡聚类算法。

平衡聚类算法的主要思想是以每一个非空单元网格为基准，在其8-邻域内开通连通区间。若其8-邻域内存在非空单元网格，则将其连通，并且以新连通的单元网格为基准，开辟新的连通区间直致无法开辟新的连通区域为止。此外，若最终形成的连通域的边缘存在过密或过稀的单元网格，将影响到聚类中心的预选取，因此将游离该单元网格;若最终形成了K个连通域，将K值作为接下来K-均值聚类的类簇数，并计算每个连通域的城市分布均值，将其作为K-均值聚类的初始聚类中心。

2 免疫遗传算法

传统的遗传算法［5－8］是一种具有“生成 +检测”的迭代过程的搜索算法。从理论上分析，迭代过程中，在保留上一代最佳个体的前提下，遗传算法是全局收敛的［9］。然而，在对算法的实施过程中不难发现，两个主要遗传算法是模拟生物体的免疫系统算子，其都是在一定发生概率的条件下，随机地、没有指导地迭代搜索，因此它们在为群体中的个体提供了进化机会的同时，也不可避免地产生了退化现象。在某些情况下，这种退化现象还相当明显。每一个待求的实际问题都会有自身一些基本的、显而易见的特征信息或知识。遗传算法的交叉和变异算子却相对固定，在求解问题时，可变的灵活程度较小。这对算法的通用性无疑是有益的，但却忽视了问题的特征信息对求解问题时的辅助作用，特别是在求解一些复杂问题时，这种“忽视”所带来的损失往往就比较明显了。

针对这些问题，提出一种新的算法——免疫遗传算法(immune genetic algorithm，IGA)［10］。该算法借鉴生物免疫系统的自适应识别和排除侵入机体的抗原性异物等性能，将生物免疫系统的学习、记忆、多样性和识别的特点引入遗传算法。在保留遗传算法优良特性的前提下，该算法力图有选择、有目的地利用待求问题中的一些特征信息或知识，以抑制其优化过程中出现的退化现象。

2.1 免疫算子

本文所提出的免疫思想主要是在合理提取疫苗的基础上，通过接种疫苗和免疫选择两个操作步骤来完成的。前者是为了提高适应度，后者则为了防止群体的退化。

①接种疫苗

设个体x，给其接种疫苗是指按照先验知识来修改x的某些基因位上的基因，使所得个体以较大的概率具有更高的适应度。首先考虑以下两种特殊情况:其一，若个体y的每一基因位上的信息都是错误的，即每一位码都与最佳个体不同，则对任一个体x，其转移为y的概率为0;其二，若个体x的每个基因位都是正确的，即x已经是最佳个体，则下一代个体将完全复制上一代的最佳个体基因。此外，设有群体c=(x1，x2，…，xn0)，对 c 接种疫苗是指在c中按比例a随机抽取na=an(0＜a≤1)个个体而进行的操作。疫苗是从对问题的先验知识中提炼出来的，它所包含的信息量及其准确性对算法的性能起着重要的作用。

②免疫选择

这一操作分两步完成。第一步是免疫检测，即对接种了疫苗的个体进行检测，若其适应度仍不如父代，说明在交叉、变异的过程中出现了严重的退化现象。这时该个体将被父代中所对应的个体所取代;如果子代适应度优于父代，则进行第二步处理。第二步是退

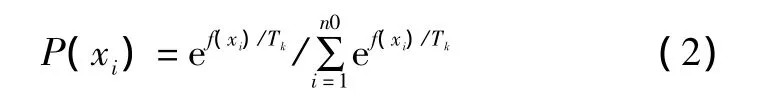
式中:f(xi)为个体xi的适应度;{Tk}为趋近于0的温度控制序列。

2.2 免疫遗传算法

免疫遗传算法流程如图1所示。火选择，即在目前的子代群体Ek=(x1，…，xn0)中以概率P(xi)选择个体xi进入新的父代群体。

图1 免疫遗传算法流程图Fig.1 Flowchart of the immune genetic algorithm

3 城市群间货物配送算例

城市群间货物配送时的路径选择问题是一个难解问题，可以使用演化算法求解。当节点很多时，使用演化算法则不可避免地要解决计算速度慢、求解成功率低等问题。

本文提出的基于平衡聚类的免疫遗传算法大体上分为两个阶段:第一阶段是要将所有的城市按照地理分布情况聚成K类，并找出类与类间相隔最近的点;第二阶段是在已聚成的类中采用免疫遗传算法寻求类中的最短城市路径。具体介绍如下。

第一阶段:采用平衡聚类将样本城市聚类，此处取城市数量为50，聚类数为3。聚类后找出类间最短距离，即找到两类间相聚最近的两点。类间最短路径如图2所示。

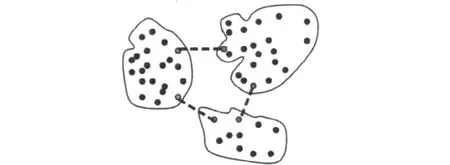
图2 类间最短路径Fig.2 The shortest route among clusters

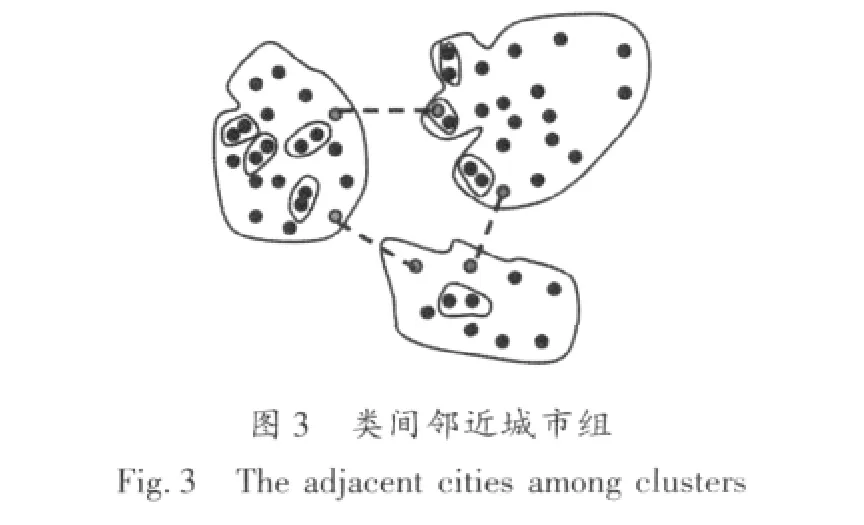
第二阶段:在已聚成的每一个类中用免疫遗传算法寻求最短路径。此处取类一为例。在确定了首尾城市后，即类一城市群的路线为{c1，…，c2}。根据先验知识抽取免疫疫苗，类一中相邻较近的城市组有(c4，c12)、(c23，c9)、(c42，c18)及(c13，c6)，其示意如图 3 所示。因此，经免疫遗传算法后类一的路径为{c1，…，c4，c12，…，c23，c9，…，c42，c18，…，c13，c6，…，c2}。以此类推其他几类内部城市路径，最终得出所有城市的路径，其示意图如图4所示。

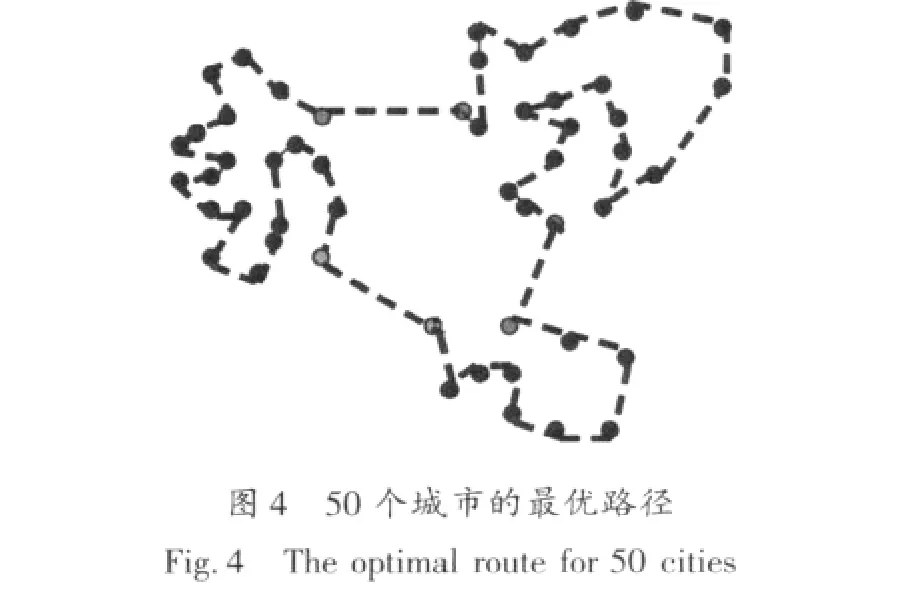
4 算法仿真

采用 CHN144数据，在 Core 2 GHz、0.99 GB 内存的计算机上，分别进行传统遗传算法及基于平衡聚类的免疫遗传算法的仿真。将两种算法分别仿真5次，每次仿真得到最优解的时间如表1所示。

表1 数据仿真结果Tab.1 Simulation result

从表1可知，经5次仿真后，传统遗传算法在寻求到最优解时所耗的平均时间为27.59 s，而本文算法平均时间为6.9 s。因此，在具有簇类特征的城市群间寻求最短路径问题上，基于平衡聚类的免疫遗传算法的收敛速度较传统的遗传算法提高了近3倍。

5 结束语

本文通过聚类与免疫遗传算法的结合，不仅在具有簇类特征的城市群货物配送路径选择问题上加快了算法的收敛速度，而且还在遗传算法的基础上，增加了多样性保持、免疫记忆和免疫选择的机制，这样能使算法收敛速度更快，而多样性的保持增强了算法全局搜索能力。通过对CHN144数据的试验后，证明了本文的基于平衡聚类的免疫遗传算法的可行性，尤其对于具有明显稠密度的地理分布的大样本数据，算法的收敛速度较传统的优化算法有更显著的提高。

［1］熊盛武，李程俊.基于机群的求解TSP问题的分布式演化算法［J］.小型微型计算机系统，2003，24(6):959 －961.

［2］刘宏兵，熊盛武.基于模糊C-均值聚类的TSP演化算法［J］.计算机工程与应用，2006(8):32－27.

［3］Sun Y，Lu Y.A scalable grid-based clustering algorithm for very large spatial databases［C］//Proceeding of the International Conference on Computational Intelligence and Security，2006:763 －768.

［4］米源，杨燕，李天瑞.基于密度网格的数据流聚类算法［J］.计算机科学，2011(12):54－59.

［5］Huang Z.Extensions to the k-means algorithm for clustering large data sets with categorical values［J］.Data Mining and Knowledge Discovery II，1998(2):283 － 304.

［6］陈国良，王煦法，庄镇泉，等.遗传算法及其应用［M］.北京:人民邮电出版社，1996.

［7］周明，孙树栋.遗传算法原理及其应用［M］.北京:国防工业出版社，1996.

［8］莉维茨.演化程序—遗传算法和数据编码的结合［M］.北京:科学出版社，2000.

［9］Rudolph G.Convergence analysis of canonical genetic algorithms［J］.IEEE Transactions on Neural Networks，1994，5(1):96 －101.

［10］蔡自兴，龚涛.免疫算法研究的进展［J］.控制与决策，2004(8):18－23.