型函数极限求解方法的总结归类

刘 浪

（长沙医学院 计算机系，长沙 410219）

1 利用函数的连续性求解

函数连续是函数极限的一种特殊情况，我们总结的相关结论有：1）初等函数在其定义域内都是连续的；2）在连续的前提下，极限值等于函数值.由此我们可以知道，当我们要求型函数的极限时，只要判断这点x0是否在定义域内，如果在定义域内极限值则等于函数值，例如：

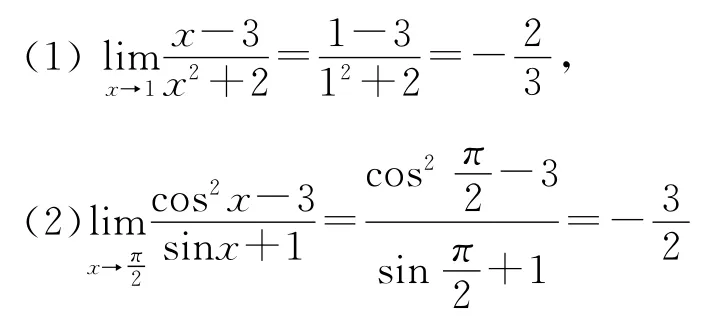
2 利用恒等变形求解

当x0不在定义域里的时候，我们就要根据具体情况进行分析了，首先可以考虑是否能够利用恒等变形使得x0在变形后的函数定义域里，再利用连续性求解；一般用的比较多的恒等变形有：分母有理化、平方差公式、立方差公式、倍角公式、和差化积等.例如：

3 利用两个重要极限及无穷小量的知识求解

如果恒等变形之后，x0仍不在定义域里，或者不能进行恒等变形，那么我们就可以考虑能否用两个重要极限及其变形形式和无穷小量的知识（最主要的是等价无穷小）：x→0时，sinx～x，tanx～x，arcsinx～x，1－

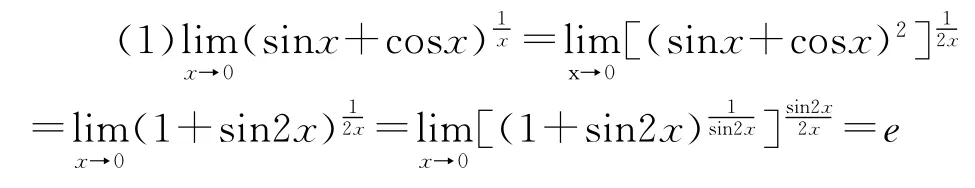
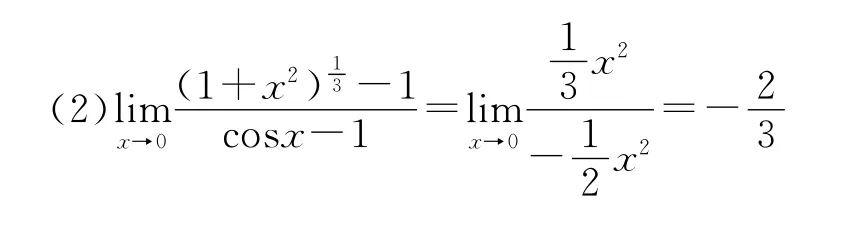
4 利用L′Hospital法则求解

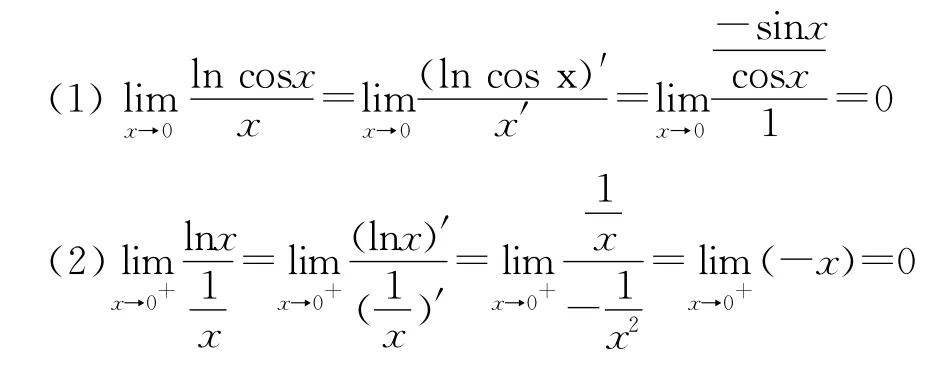
5 综合运用

对于有些复杂的题目，利用上面所说的某一个方法，我们可能就无法解决了，我们需要综合上面的几个方法，所以这就需要我们不断练习，才能灵活的运用不同方法解题.例如：

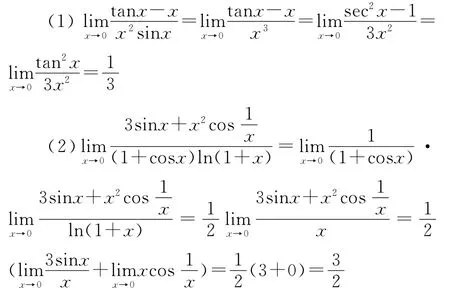
［1］张惠安.医用高等数学［M］.人民邮电出版社，2012.

［2］同济大学数学系.高等数学（第六版）［M］.高等教育出版社，2008.