多元函数微分学中的一个注记
贾武艳,王慧蓉
(长治学院 数学系,山西 长治 046011)
1 预备知识
定义1设函数y=f(x)定义在点x0的某领域内.当给 x0一个增量 Δx,x0+Δx∈U(x0)时,相应地得到函数的增量为Δy=f(x0+Δx)-f(x0)。如果存在常数A,使得Δy=AΔx+oΔx,则称函数f在点x0可微。
定义2设函数z=f(x,y)定义在点P0(x0,y0)的某领域 c 内。对于 U(P0)中的点 P(x,y)=(x0+Δx,y0+Δy),若函数f在点P0处的全增量Δz可表示为:
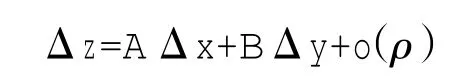
其中 A,B是仅与点 P0有关的常数,ρ=,则称函数f在点P0可微。
定义3 设D⊂Rn为开集,x0∈D,函数f:D→Rm。如果存在线性算子A(只依赖于x0),使得x∈∪(x0)⊂D 时,有:
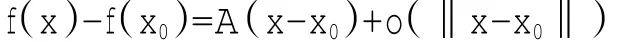
则称函数f在点x0可微。
引理1[1-3](极限值与函数值的关系)若函数f(x)在点x0处的极限值为A,则存在x0的某领域U(x0)内,有f(x)=A+α,其中α→0(Δx→0)。
引理2若函数f(x,y)在点P0(x0,y0)处的极限值为A,则存在某U(P0),使得在该领域内有f(x,y)=A+α,其中 α→0(Δx→0,Δy→0)。
2 主要结论
定理1函数y=f(x)定义在点x0可微,存在某U(x0),则在该领域内函数增量
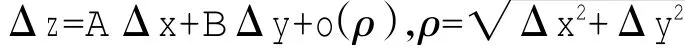
Δy=f(x0+Δx)-f(x0)=AΔx+αΔx其中 A 是常数,α→0(Δx→0)。
证明:若函数y=f(x)在点x0可微,则存在常数A,使得 Δy=AΔx+o(Δx).下面说明 αΔx=o(Δx),α→0(Δx→0)。事实上,,故 αΔx⊂o(Δx),另外,任取f(Δx)∈o(Δx),则,根据极限值与函数值的关系可知存在ε→0(Δx→0),使得f(Δx)=εΔx。故αΔx=o(Δx)。证毕
定理2函数z=f(x,y)定义在点P0(x0,y0)可微,存在某P0(x0,y0),则在该领域内函数增量
Δz=AΔx+BΔy+αΔx+βΔy
其中 A,B 是常数,α→0,β→0(Δx→0,Δy→0)。
证明:若函数z=f(x,y)定义在点P0(x0,y0)可微,则存在常数A,B,使得:
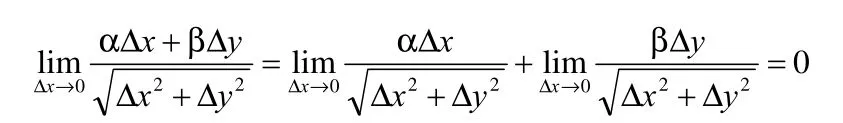
下面说明 αΔx+βΔy= (ρ),α,β→0(Δx,Δy→0)。事实上,根据无穷小量和有界量的关系可知,则α∆x+β∆y⊂o(ρ)。另外,任取f(∆x,∆y)∈o(ρ),则,根据极限值与函数值的关系可
知,存在ε→ 0 (∆x,∆y→0),使得
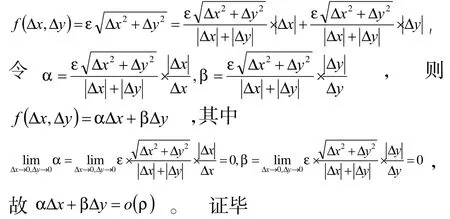
定理3 设D⊂Rn的为开集,x0∈D,向量函数f:D→Rm在点x0可微,存在线性算子A(只依赖于x0),使得 x∈∪(x0)⊂D 时,有

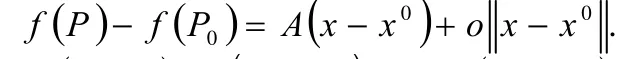

再说明一般情况下,设向量函数f:D→Rm在点x0可微,则存在线性算子A(只依赖于x0),使得x∈∪(x0)⊂D 时,有:
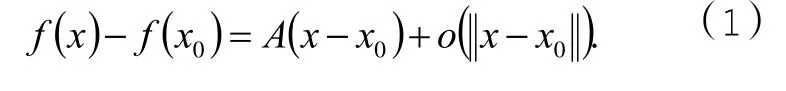

那么,(1)式等价于
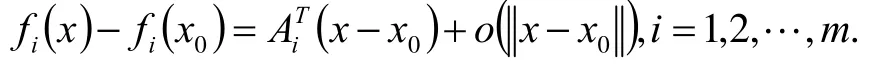
由上述m=1情况得知,存在Bi,使得
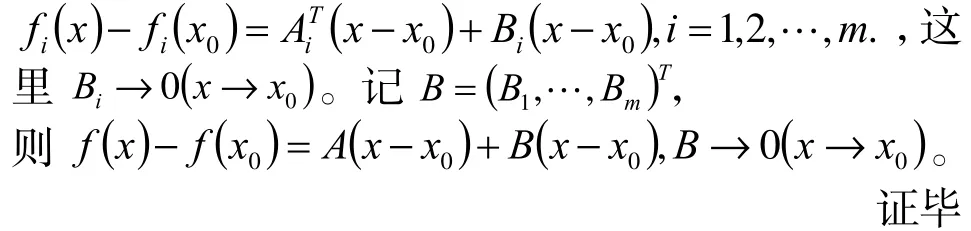
可知,向量函数f在(1,1)处可微。并且有
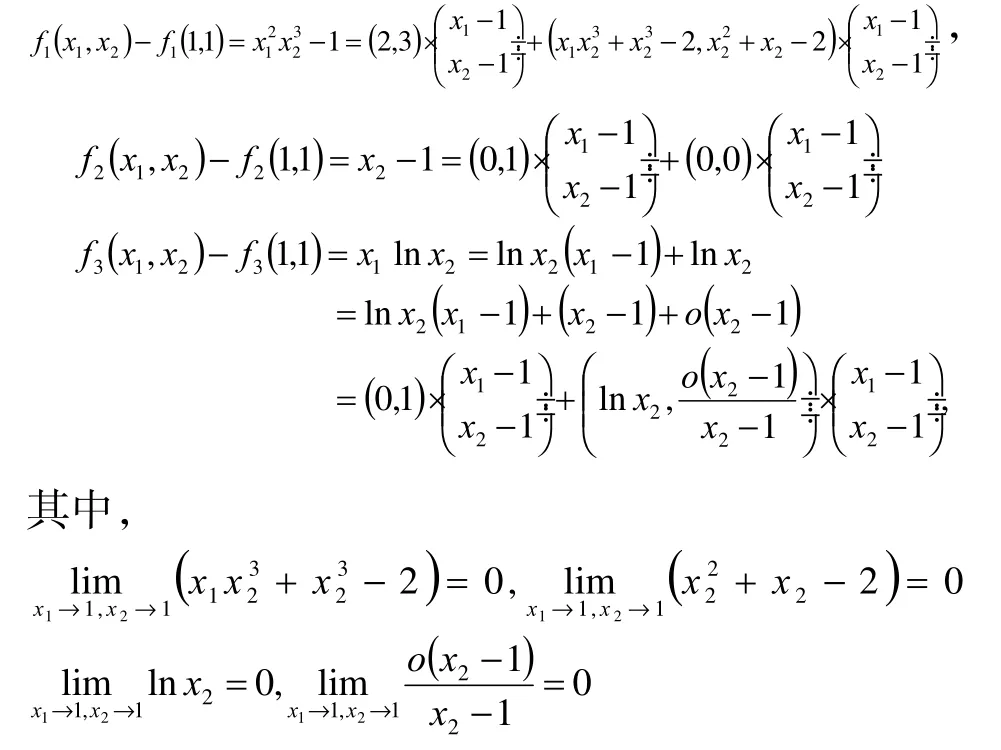
3 总结
学生在学习函数微分定义的时候,常常只注重对微分推广公式[1-3]的应用,却往往忽略其证明,并且对于高阶无穷小量的多种形式欠缺思考,文章通过利用函数值与极限值的关系重新证明函数可微下的一个公式并将其推广到多元函数的微分学[4]中,并让学生更加理解高阶无穷小量是一个集合并非一个确定的函数。

