挠性航天器滑模变结构控制及抖振抑制研究*

钟晨星,郭 毓,周 川,陈庆伟

(南京理工大学自动化学院，南京 210094)

随着航天技术的发展，现代航天器通常采用中心刚体加挠性附件的典型结构.这类航天器在飞行和控制中,随着挠性附件的伸展和收缩，航天器的转动惯量变化很大，同时还受到外部干扰力矩的作用,这些因素使得航天器对象具有很大的不确定性.而且，在此过程中,由于中心刚体和挠性附件之间存在强耦合,姿态运动常常导致挠性结构的持续振动,进而影响航天器的姿态运动与控制.因此,在设计挠性航天器姿态控制律时,寻求一种既能进行姿态控制又能抑制挠性结构振动的强鲁棒性控制方法就显得尤为重要.滑模变结构控制由于具有良好的鲁棒性和处理非线性问题的独到优点，在航天器姿态控制上得到了广泛的应用[1-3].Vadali[4]成功地将变结构控制理论引入到刚体航天器的姿态大角度机动中.Lo和Chen[5]提出了一种通用的航天器姿态滑模控制方法，但初始时刻输出力矩较大，容易激起挠性体弹性振动.滑模控制虽然具有良好的鲁棒性，但其本质上的开关特性也会带来抖振这一突出问题，而且控制量的抖振又会激发航天器姿态和挠性附件的振动，影响控制精度.对此，不少学者采用“边界层法”和引入模糊技术对其进行改进.文献[6]用饱和函数代替符号函数以减弱抖振，对于刚体航天器有较好的控制效果，但是对于挠性航天器仍然会激发挠性附件的持续振动，从而影响航天器姿态的稳定度.管萍等[7]将自适应模糊变结构控制方法应用到航天器的姿态稳定控制中，通过引入模糊控制技术抑制抖振，但其控制算法较为复杂.

针对上述问题，本文改进了滑模变结构控制中的“边界层”法，设计了一种改进的滑模变结构控制器以抑制抖振.在建立挠性航天器数学模型的基础上，采用Lyapunov方法设计姿态滑模变结构控制律.针对滑模变结构控制的不连续特性引起的抖振，提出采用反正切函数代替“边界层”法中的饱和函数；为柔化控制量和避免机动初始时刻控制力矩过大引起航天器本体姿态的振动和激发挠性附件振动，在滑模控制器的到达控制律中引入滞后因子.最后，将所提控制算法用于挠性航天器的三轴姿态机动与稳定控制中，仿真结果验证了算法的有效性.

1 挠性航天器模型

采用四元数法描述航天器姿态，其运动学方程为[8]

(1)

挠性航天器姿态动力学方程和挠性附件振动方程分别为[8]

(2)

(3)

其中：J∈R3×3为航天器转动惯量，u∈R3×1为控制力矩，δ∈Rn×3为航天器本体与挠性附件振动的耦合矩阵，η∈Rn×1为挠性附件振动的模态坐标，ζ∈Rn×n为挠性附件振动阻尼比矩阵，Λ∈Rn×n为挠性附件振动频率矩阵，d∈R3×1为干扰力矩矢量，符号ω×表示矢量ω的斜对称矩阵.

(4)

假设期望姿态四元数为qd，则姿态误差四元数定义为[8]

(5)

式中，关于四元数p和q的4×4矩阵均为正交矩阵，且可逆.

假设期望姿态角速度为ωd，姿态角速度误差定义为

ωe=ω-ωr

(6)

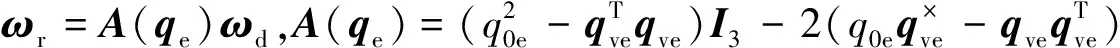
(7)

由式(4)～(7)可得，航天器姿态误差方程

(8)

(9)

2 滑模变结构控制器设计

2.1 滑模控制律设计

根据航天器姿态数学模型，定义切换函数为[5]：

s=ωe+kqve

(10)

式中：s=[s1,s2,s3]T∈R3,k=diag{k,k,k}，k>0.

滑动模态的存在是使用滑模变结构控制的前提，即需要满足下列到达条件：

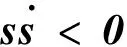
(11)

针对非线性的挠性航天器姿态动力学方程(8)，设计滑动模态控制律u为：

u=-K1s-D1F(s)+ueq

(12)

式中：K1=diag{ki}，D1=diag{di}，ki>0，di>0，i=1,2,3，F(s)={sgn(s1),sgn(s2),sgn(s3)}T，此处，sgn(si)为符号函数.

(13)

证明.将滑模到达条件式(11)，表达成Lyapunov函数型条件，选取Lyapunov函数为：

(14)

对其求导，可得：

将式(12)代入上式，可得：

利用边界层法对所设计控制律(12)做改进，用饱和函数替换符号函数，所得控制律为

u=-K1s-D1F1(s)+ueq

(15)

式中：F1(s)=[sat(s1),sat(s2),sat(s3)]T,，此处，sat(si)为饱和函数，K1和D1为正定对角阵.

2.2 改进滑模控制律设计

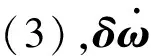
设计改进控制律为：

u=-aK1s-D1F2(s)+ueq

(16)

其中：a=diag{ai},(i=1,2,3)，ai=(1+ε-e-βt)，滞后因子数值从ε开始以指数函数形式趋近于1，趋近于1后，对控制不再起滞后作用.β数值的大小决定滞后作用的长短，β数值越大滞后作用越短，经过多次仿真，当β=0.1时，系统综合性能指标较好.ε为很小的数，主要避免机动初始时刻滞后因子数值为0的情况，此处选择为ε=0.001.f(si)为改进的“反正切”函数，F2(s)=[f(s1),f(s2),f(s3)]T

(17)

采用更加光滑的“反正切函数”替代“饱和函数”渐变段，减小滑模控制带来的抖振，使控制量更加柔化，减小由此引起的航天器本体和挠性附件的振动，提高控制精度.针对挠性航天器在机动初始时刻误差较大、控制量幅值较大，容易引起超调和航天器本体姿态和挠性附件的振动.加入利用指数函数设计的滞后因子：ai=(1+ε-e-βt)，避免初始误差较大带来的超调，减小最大控制力矩和由此引发的航天器振动，并且降低对执行机构要求，从而减小执行机构体积和质量.在经历机动初始阶段后，随着时间的增长，滞后因子数值接近于1，滞后作用逐渐减弱并消除，控制律又回到原本的滑模控制，航天器继续以较快的速度进行机动，控制量幅值明显降低，而且控制量输出更加柔化，变化更加平稳.

3 仿真研究

利用MATLAB/Simulink软件对航天器进行姿态机动和稳定控制进行仿真，检验所提控制方法的有效性.航天器的标称转动惯量阵为[10]：

挠性附件与航天器本体姿态的耦合矩阵：

挠性附件的标称振动频率阵：

Λ0=diag{1.02464,1.23670,1.91610,

2.85637,3.87904}(rad/s)，

挠性附件振动阻尼阵：

ξ=diag{0.001,0.001,0.001,0.001,0.001}，

控制器参数选择为：

K1=diag{1500,1500,1500},

D1=diag{0.95,0.95,0.95}.

取航天器实际转动惯量J=J0，挠性附件振动频率Λ=Λ0.初始姿态欧拉角为[0° 0° 0°]T，期望姿态欧拉角为[10° -10° 10°]T，初始和期望姿态角速度均为[0 0 0]T(°)/s，不考虑外部干扰即d=0，控制力矩限幅±100N·m.采样时间ts=0.1s，仿真时间长度tf=150s.采用本文所提改进滑模控制(ISMC)算法(16)的仿真结果如图1所示.为进行对比，在相同条件下，采用边界层滑模控制(BLSMC)算法(15)的仿真结果如图2所示.

(a)姿态角响应曲线

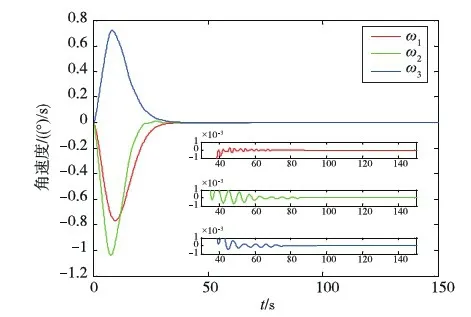
(b)姿态角速度响应曲线

(c)挠性附件振动模态

(d)控制力矩

对比图1(a)和图2(a)可知，两种算法均能完成姿态机动任务，改进的滑模控制律在机动速度上略有下降，但机动路径更加平稳；对比图1(a)、(b)与图2(a)、(b)可知，改进后的滑模控制律能够使姿态角误差和姿态角速度误差更快进入±(1×10-3)稳态误差带且稳态误差更小，而且机动所需最大速度也更小，更加平稳；对比图1(c)和图2(c)可以看出，算法改进后有效地抑制了挠性附件振动，将振动幅值减小了约一个数量级；对比图1(d)与图2(d)可见，完成相同机动任务，边界层滑模控制算法所要求的最大控制力矩几乎是改进滑模控制算法所要求最大控制力矩的10倍；由此可见使用“反正切”函数替代饱和函数，实现了对控制量的柔化和抖振的抑制，有效地减小了姿态的振动，显著提高了航天器机动后的指向精度和稳定度.加入滞后因子明显减小了所需最大控制力矩，柔化了控制力矩，减小了由此引起航天器姿态和挠性附件的振动，控制精度更高.

为考察算法对系统参数摄动的鲁棒性，当转动惯量和模态振动频率摄动±20%时，其它条件不变，分别进行机动仿真,仿真结果如下表1与表2所示.

(a)姿态角响应曲线

(b)姿态角速度响应曲线

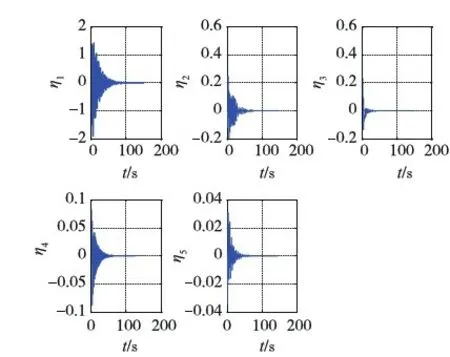
(c)挠性附件振动模态

(d)控制力矩

为便于对比，定义如下几项性能指标：机动时间：单轴姿态角进入稳态值与期望值之差的±0.5%角误差带的时间，；稳定时间：航天器单轴角速度进入稳态值与期望值之差的±0.1%角速度误差带；指向精度：机动90s后单轴姿态角误差的均方值；稳定度：机动90s后单轴姿态角速度的均方值.

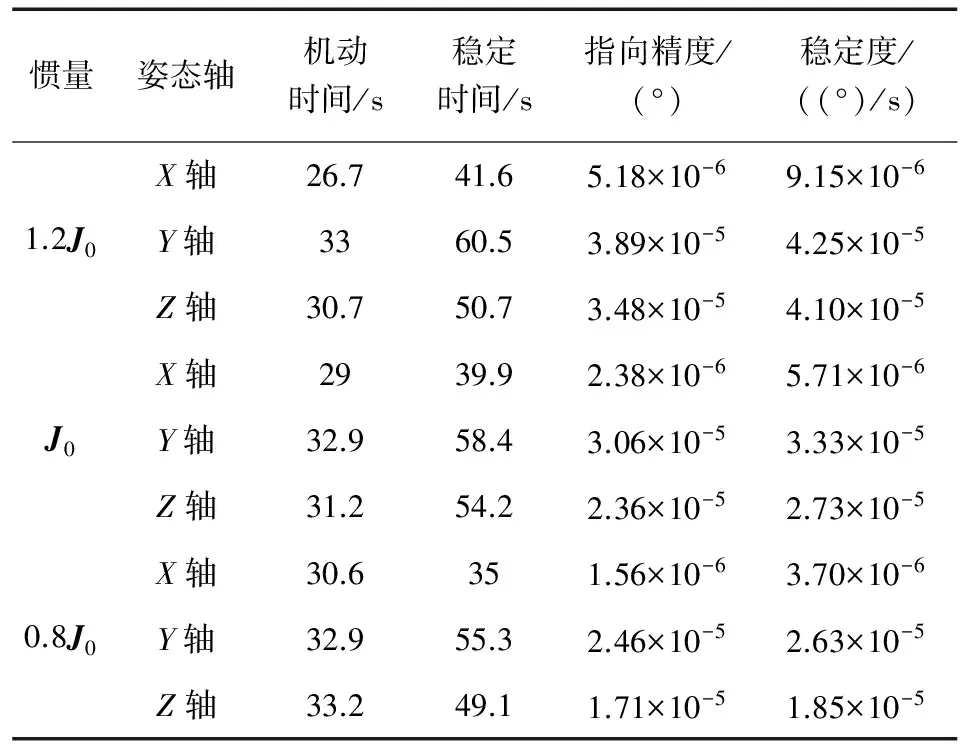
表1 改进滑模控制对不同惯量参数下鲁棒性

由表1中改进滑模控制的性能指标和可知，当航天器惯量J=1.2J0、J=0.8J0时,系统的控制性能与惯量J=J0指标变化不大，说明改进滑模控制对转动惯量的变化具有较强的鲁棒性.

由表2中改进滑模控制的性能指标和可知，当航天器模态振动频率摄动±20%时，系统的控制性能与Λ=Λ0时指标变化不明显，表明改进滑模控制对模态振动频率的摄动具有良好的鲁棒性.

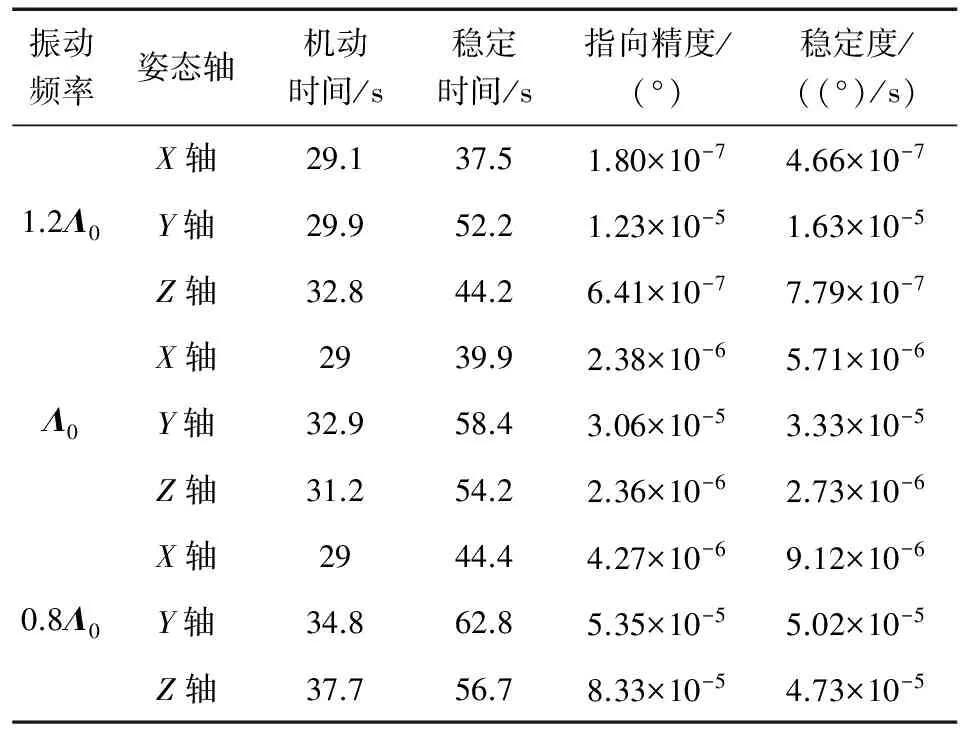
表2 改进滑模控制对不同模态振动频率参数下鲁棒性

4 结 论

本文研究了挠性航天器姿态的滑模控制问题，基于Lyapunov方法，提出了一种改进的滑模控制器设计方法.在该滑模控制器中，采用更为光滑的“反正切”函数代替饱和函数以抑制“抖振”现象，在到达运动控制律中引入滞后因子以减小最大控制力矩和柔化控制量.对挠性航天器姿态机动控制的仿真结果表明，采用本文所设计的改进滑模控制器，能够削弱抖振，提高姿态机动的快速性和控制的稳定度，抑制了挠性附件的振动；减小控制力矩最大幅值，柔化控制量，大大降低了对执行机构最大输出力矩的要求，从而避免了大控制力矩所引起的挠性附件振动.此外，该控制器对航天器自身参数的不确定具有良好的鲁棒性.

参 考 文 献

[1]Hu Q L, Ma G F, Xie L H. Robust and adaptive variable structure output feedback control of uncertain systems with input nonlinearity[J]. Automatica, 2008, 44(2): 552-559

[2]Hu Q L, Ma G F. Control of three-axis stabilized flexible spacecraft using variable structure strategies subject to input nonlinearities[J]. Journal of Vibration and Con-trol, 2006, 12(6): 659-681

[3]Liu H, Li J F, Hexi B Y．Sliding mode control for low thrust earth-orbiting spacecraft formation maneuvering [J]． Aerospace Science and Technology, 2006, 10(7):636-643

[4]Vadali S R. Variable structure control of spacecraft large attitude maneuvers[J]．Journal of Guidance, Control and Dynamics, 1986, 9(3):235-239

[5]Lo S C, Chen Y P．Smooth sliding mode control for spacecraft attitude tracking maneuvers[J]．Journal of Guidance, Control and Dynamics, 1995, 18(6):1345-1349

[6]吕建婷,李传江,马广富.卫星姿态调节的滑模PID控制器设计[J].哈尔滨工业大学学报,2008,40(7): 1009-1012

Lv J T,Li C J,Ma G F. A sliding mode PID controller design for satellite attitude regulation[J].Journal of Harbin Institute of Technology, 2008, 40(7): 1009-1012

[7]管萍,刘小河,刘向杰.挠性卫星的变结构姿态控制[J].控制理论与应用,2007,24(3):480-484

Guan P, Liu X H, Liu X J. Variable structure attitude control of flexible spacecraft [J]. Control Theory & Applications, 2007, 24(3): 480-484

[8]屠善澄.卫星姿态动力学与控制[M].北京：中国宇航出版社,1999

[9]Hu Q L. Variable structure maneuvering control with time-varying sliding surface and active vibration damping of flexible spacecraft with input saturation[J]. Acta Astronautica,2009,64:1085-1108

[10]李英波.挠性充液卫星动力学分析与姿态控制研究[D].上海:上海交通大学,2001

Li Y B. Studies on attitude dynamics and control for flexible satellite filled with liquid[D]. Shanghai: Shanghai Jiaotong University, 2001