三轴零动量卫星在轨转偏置动量控制的设计与实现

袁 军，魏 懿，王 哲，王淑一，傅秀涛，王新民，王胜刚，周剑敏

(北京控制工程研究所，北京 100190)

资源一号卫星的姿态与轨道控制系统(AOCS，attitude and orbit control system)是一个整星零动量自主冗余控制的三轴稳定轮控系统[1].该系统具有性能指标高、系统复杂、技术难度大、国产化部件多、自主功能强、在轨维护方便等特点，是中国研制成功的卫星中较复杂的姿态与轨道控制系统.

资源一号02B卫星设计寿命为两年，在轨正常运行一年后，主份陀螺发生故障.该卫星主备份陀螺均为3个正交安装的速率积分陀螺，在只剩下3个备份的液浮陀螺情况下，任何一个陀螺故障将导致卫星控制系统失效.为了确保卫星的安全可靠运行，提出了关闭备份陀螺，将三轴零动量控制方式的资源一号02B卫星转为俯仰轴轮控加磁控的偏置动量控制方式，采用角动量反馈，对俯仰轴所需轮控电压进行计算；对磁控电压进行计算，同时计算俯仰动量轮卸载所需磁力矩器电压.设计了相应的控制算法，并根据控制算法进行了控制软件的设计、验证和实施，卫星成功转入了俯仰方向偏置动量控制加磁控的控制模式，关闭了备份陀螺，确保了卫星长寿命运行.卫星转控制模式后，姿态控制精度和姿态稳定度良好，达到了预期目的，为三轴零动量卫星控制系统在陀螺或动量轮故障下保证卫星稳定可靠运行提供了一种设计方案，该思想在后续的同类卫星控制系统中得到了广泛应用.

1 系统组成

资源一号卫星姿态轨道控制系统采用了整星零动量自主冗余控制的三轴零动量稳定轮控系统.系统由敏感器、执行机构和控制器组成.其中敏感器包括：

1)2个圆锥扫描红外地球敏感器，分别沿卫星本体坐标系的+X、+Y轴安装，测量卫星滚动角和俯仰角.

2)2组(互为备份)3个正交安装的速率积分陀螺，可测量卫星三轴的角速度.

3)3种太阳敏感器.其中，2个数字式太阳敏感器的狭缝正交，可以测出太阳矢量在星体的方位，与地球敏感器联合确定卫星三轴姿态；帆板上的2个模拟式太阳敏感器可测出太阳在模拟太阳敏感法平面投影与帆板法线的夹角，提供帆板目标转角，用于帆板对日跟踪控制；1个装在星体上的模拟式太阳敏感器狭缝平行于星体滚动轴，与地球敏感器测量联合可以确定卫星三轴姿态，并以模拟信号方式作为模拟线路控制器的输入，在应急模式下使用.2个0-1式太阳敏感器分别安装在星体的+X和-X面，在4π立体角范围内提供太阳方位信息，用于太阳捕获.

4)2路星敏感器[2]，这是资源一号02B卫星中新增加的，安装在卫星的+Y面上，测量数据仅作为有效载荷辅助数据以提高定位精度.

控制系统的执行机构包括：

1)16个1N推力器，可提供3个方向的控制力矩；2个20N的推力器，分别沿-X和+Y轴安装，用于轨道控制和轨道维持.

2)4个偏置动量轮，3个分别安装在X、Y、Z轴，第4个倾斜安装，组成一个整星零动量的轮控系统，提供姿态控制力矩.

3)3个正交安装的磁力矩器，可对动量轮进行卸载.

4)1个帆板驱动机构，对单翼太阳电池帆板进行控制，使其法线指向太阳.

控制器包括：

1)AOCC，采用模块级双机冷备份冗余结构.为了提高系统的故障识别能力，在主要的敏感器及帆板驱动机构和推进系统中均采用智能终端单元，进行辅助信息处理.

2)应急线路，由模拟线路构成，以便在星载计算机暂时失效时使太阳帆板对准太阳，保证整星的能源供给.

3)姿轨控配电器，负责姿轨控系统内部各个部件的电源控制.

2 动量交换卫星姿态动力学方程

整星角动量Hs=H+h，第一项为卫星本体的角动量H=Iω，第二项为飞轮转动部件相对星体的合成角动量沿本体坐标系的分量h=[hx,hy,hz]T，取星体主惯量轴为本体坐标系，考虑到惯量积很小的情况下，惯量阵为对角阵I=diag{Ix,Iy,Iz}.带动量装置的卫星姿态动力学方程[3]的一般式为

(1)

(2)

由上述姿态动力学方程可知，三轴稳定卫星姿态运动的特点与动量装置给出的角动量及其沿三轴的分布有关.当卫星为三轴零动量控制时，忽略二阶小项，姿态动力学方程简化为

(3)

三轴零动量控制时，引入解耦律、磁力矩器卸载使动量轮的角动量保持在适当的范围，在不进行喷气控制时，得3个独立姿态动力学方程：

(4)

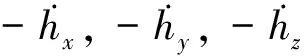
为了实现卫星从零动量控制到偏置动量控制的切换，必须确保卫星在偏置动量控制下具有陀螺定轴性,动量装置的角动量应满足[3]：

(5)

偏置动量控制加磁控时，飞轮转动部件相对星体的角动量h=[0,-hb,0]T，简化姿态动力学方程为

(6)

俯仰通道设计与零动量控制一致，而滚动—偏航通道的设计要根据姿态信息、控制动量自由度的多少，采用不同控制律达到进动控制与章动阻尼.

3 控制器设计

根据式(6)给出的卫星姿态动力学方程，俯仰通道采用PID控制，由于俯仰轮角动量稳定在标称值附近，俯仰角速度与角动量偏差成比例关系，因此可引入动量轮角动量偏差作为角速度反馈信息，俯仰轴控制器输出为

(7)

(8)

(9)

(10)

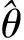
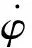
(11)

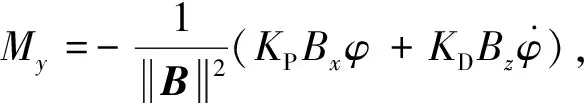
(12)

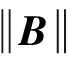
式(12)提供了系统所需的章动阻尼力矩与进动力矩，当BxBz>0时有增大刚度的作用.Bx和Bz一般是根据简化的地磁场模型与轨道计算及坐标转换求得，在极区附近Bx过零时很难保证极性的正确性，工程上的解决办法是在过零区设计一个死区，不进行磁控.

最后给出章动阻尼及进动控制磁矩My的计算公式为

(13)

用于磁卸载的磁矩Mx,Mz计算公式为

(14)

(15)

屏蔽原有的三轴零动量控制程序以及磁力矩器卸载程序，通过式(13)的算法实现滚动—偏航轴的进动控制及章动阻尼，并对俯仰飞轮进行磁卸载.

4 稳定性分析

(1)俯仰通道稳定性

卫星关闭陀螺后，采用红外地球敏感器测量俯仰姿态角.俯仰通道采用动量轮控制，俯仰通道的反馈控制回路框图如图1.

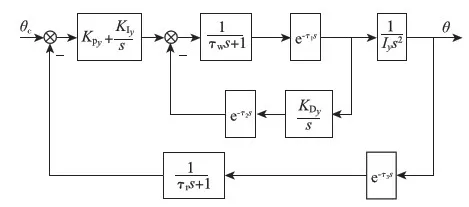
图1 俯仰通道的反馈控制回路框图

图1中τw是动量轮响应时间常数，τr是角速度反馈的时间常数，τ1,τ2,τ3是各环节采样时间常数.根据卫星控制系统参数，分析俯仰控制的稳定性.图2为俯仰通道控制系统开环波特图，从图中可知幅值裕度约为14.8dB，相位裕度为46.5°.因此俯仰通道控制系统稳定.

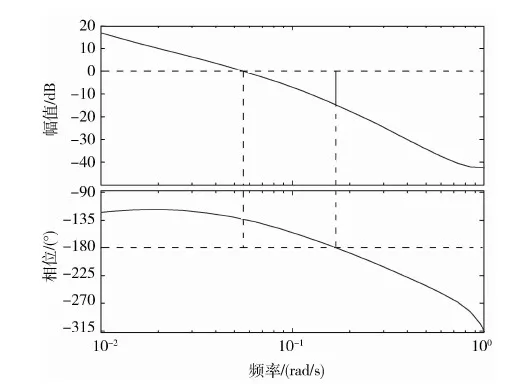
图2 俯仰通道控制系统开环波特图

(2)滚动—偏航通道稳定性

1)进动控制

进动控制主要考虑轨道运动耦合作用，忽略转动惯量和干扰力矩项，由式(11)得到进动运动方程.

(16)

(17)

根据式(16)～(17)，由式(12)中起进动控制的部分得到系统的特征方程为

C(s)=s2+as+b=0

(18)

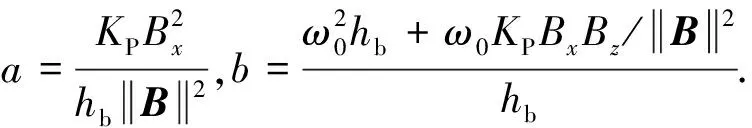
选择适当的KP，使式(18)极点都在左半平面，可保证卫星的进动控制是稳定的.

2)章动控制

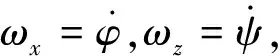
(19)

为了有效阻尼章动，必须引入角速度反馈.但系统只有滚动测量值，为此需要采用超前校正，于是式(12)中控制器引入的零点为

(20)

(21)

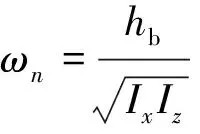
选择适当的KP,KD，当式(21)的条件满足时，可保证章动控制的稳定性.

5 实施与飞行结果

资源一号02B卫星具有对控制软件进行大范围在轨修改的能力，当卫星出现故障后，上述控制算法经充分地地面测试后，通过遥控注入成功实现了由零动量控制转为不需要陀螺信息的偏置动量控制，姿轨控分系统工作正常.

卫星转偏置动量后，只用红外地球敏感器的滚动和俯仰测量信息，依靠偏置动量控制方式保证偏航在小角度范围内变化.+Y向合成角动量可以达到-25N·m·s，满足式(5)的要求.

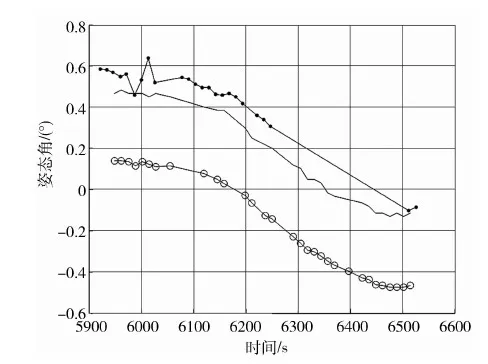
图3 滚动姿态角：星感器敏估计值(点线)、计算机姿态估计值(圈线)、滚动红外测量值(实线)

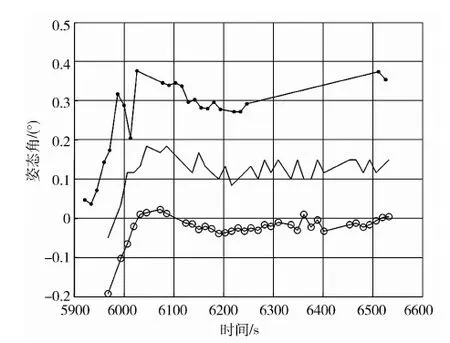
图4 俯仰姿态角：星感器敏估计值(点线)、计算机姿态估计值(圈线)、俯仰红外测量值(实线)

6 结 论

为了确保资源一号02B卫星在主份陀螺故障后卫星仍能安全可靠运行，提出了将三轴零动量控制系统转为偏置动量控制加磁控的方案.设计了相应的控制算法，通过遥控注入后，卫星成功转入俯仰偏置动量控制加磁控的控制模式，关闭了备份陀螺，姿态控制精度和姿态稳定度良好，达到了预期目的，为同类卫星控制系统的安全模式设计以及卫星在陀螺和动量轮故障下保证姿态稳定提供了一种行之有效的手段，该思想在后续的同类卫星控制系统中得到了广泛应用.

参 考 文 献

[1]王哲，姚宁，刘捷，等.资源一号卫星姿态与轨道控制系统[J].航天器工程,2008,17(增刊1):74-79

Wang Z, Yao N, Liu J, et al. CBERS attitude and orbit control system [J]. Spacecraft Engineering, 2008, 17(Supplement 1): 74-79

[2]武延鹏，黄欣，卢欣.资源一号02B卫星星敏感器[J].航天器工程, 2008,17(增刊1): 80-85

Wu Y P, Huang X, Lu X.CBERS-02B star tracker[J]. Spacecraft Engineering,2008,17(Supplement 1):80-85

[3]章仁为.卫星轨道姿态动力学与控制[M].北京：北京航空航天大学出版社，1998

[4]林来兴，潘科炎.空间飞行器控制设计准则[M].北京：科学出版社，1978

[5]Das A.The on-orbit attitude determination and control system for the Landsat-D spacecraft[C].The 20thAmerican Institute of Aeronautics and Astronautics, Aerospace Sciences Meeting, Orlando, USA, Jan. 11-14,1982