椭圆三体问题中的时间周期不变流形*

祁 瑞,徐世杰

(北京航空航天大学宇航学院，北京 100191)

相比限制性二体模型，限制性三体模型因其对空间引力资源的更深入利用，在深空探测轨道设计方面表现出巨大的应用优势.特别是平面圆型限制性三体问题(PCR3BP，planar circular restricted 3-body problem)共线平动点附近周期轨道的不变流形，以其渐近性质和运动分界特点被广泛用于平动点附近编队飞行、低能奔月以及木星多颗卫星探测等相关任务研究，并取得了一系列有价值的理论与工程实践结果[1-2].然而，这些研究只适用于自治系统PCR3BP，对于椭圆限制性三体问题(ER3BP，elliptic restricted 3-body problem )，由于不存在合适的参考系使系统摆脱对时间的显性依赖，相关研究难以推广.

对于不变流形的计算，传统的方法是用不变特征向量方向上的一条短线段来代替局部不变流形，对该线段上的点进行迭代来确定全局不变流形.然而有三方面的原因会导致数值计算出的不变流形位置不精确，时间跨度很大时尤其如此.首先，局部不变流形是利用直线段来近似的；其次，点的数值迭代有舍入误差；最后，进行高次迭代时，曲线上的点会渐渐散开.Parker和Chua[3]给出了一个较好的算法，通过沿不变流形改变点的数量，使这些点均匀分散在流形上.对于ER3BP中的时间周期不变流形，由瞬时不变集出发采用传统方法进行计算是很自然的选择.然而，Shadden等人[4]对双漩涡流场的研究结果表明，该时间周期系统的不变流形并不与瞬时不动点相连接.这说明，不变流形的传统算法在ER3BP系统中不再适用.

在流体力学领域，学者采用拉格朗日拟序结构(LCS，Lagrangian coherent structures)作为时变流场中的不变流形来研究动力系统的相空间.在较早期的文献中，LCS的定义比较模糊，给问题分析和算法设计造成不便.2001年，Haller[5]提出将LCS定义为有限时间Lyapunov指数(FTLE，finite-time Lyapunov exponent )域中的脊.有限时间Lyapunov指数是经典Lyapunov指数的变形，用于度量系统对初值的敏感依赖性，最早由Lorenz引入研究大气模型中的混沌现象.近年来，Gawlik[6]，Qi[7]等人将LCS引入天文动力学的研究并取得成功.

本文首先以单摆系统为例阐述了LCS与稳定、不稳定流形之间的关系，进而将LCS理论应用于天体力学的研究中，以质量比为0.1、偏心率为0.2的虚拟系统为例，研究了ER3BP中的时间周期不变流形，通过数值方法研究了其运动分界面本质和轨道不变特性.

1 相关的基础理论

1.1 椭圆限制性三体问题模型

假设天体M1和M2围绕其公共质心作椭圆运动，航天器在M1和M2的引力合力作用下运动，且航天器质量足够小以至于不会影响两个主天体的椭圆运动.

引入无因次量纲：长度单位DU为M2真近点角f达90°时的两主天体间距；质量单位MU为两主天体质量之和；时间单位TU为两主天体轨道周期与2π的比(本文中出现的数量，未经特殊声明，均为无因次量纲.).

建立M1-M2质心旋转脉动系：原点位于M1和M2质心；x轴由M1指向M2；y轴由x轴在轨道平面内逆时针旋转90°确定；z轴垂直于轨道面完成右手系；通过3个轴同等比例的实时伸缩，保持M1和M2质心在x轴上静止.

为了使ER3BP下的航天器运动方程与CR3BP下的方程形式相似，以f为系统自变量.在上述坐标系和无因次量纲下，容易得到航天器运动微分方程[8]：

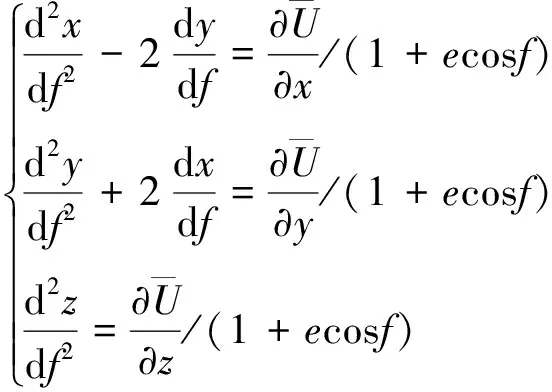
(1)

式中：

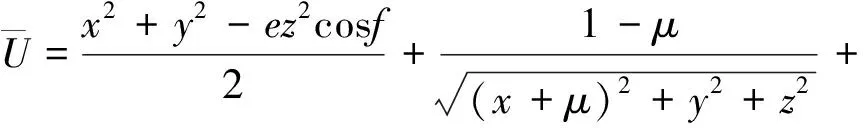
(2)

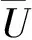
1.2 拉格朗日拟序结构

这里采用Haller的定义，将LCS定义为有限时间Lyapunov域中的脊线[5].粗略地说，FTLE就是在相流作用下，邻近的两点在有限时间内的平均最大分离速率，度量了系统对于初值的敏感依赖性.

在开区域D⊂Rn上考查动力系统：

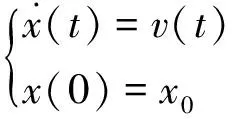
(3)

在相流映射φ的作用下，t0时刻的点x在t0+T时刻到达φ(t0+T;t0;x).假设x受到无穷小摄动δx(0)，则该摄动在t0+T时刻的变分为：

δx(T)=φ(t0+T;t0;x+δx(0))-φ(t0+T;t0;x)

(4)

只保留线性部分，得到：

(5)

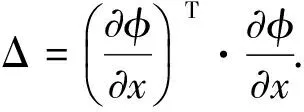
(6)

其中，λmax是矩阵Δ的最大特征值，ξ是相应于λmax的特征向量.

此时，定义有限时间Lyapunov指数为：

(7)

从而，式(6)可改写为：

(8)

对于整个定义域D，由式(7)对每一点都赋以一标量值，这就得到了FTLE域.由动力系统理论可知，不变流形位于不同侧的邻近两点会以指数速率快速分离，即不变流形对应于较大的FTLE.为此，将LCS定义为FTLE域中的脊线.分析可知，对于T>0，LCS蕴含稳定流形；对于T<0，LCS蕴含不稳定流形.

2 单摆相空间中的LCS

为了验证上述分析，考查单摆系统：

(9)

在经典的动力系统理论中，已经得到了系统(9)的相图(见图1(a)).(±π,0)是两个鞍点；(0,0)是中心.轨道a和b是连接两个鞍点的异宿轨道；轨道c是环绕中心的周期解；轨道d是旋转解.显然，异宿轨道是单摆相空间中的运动分界面，将所有轨道划分为周期解和旋转解.

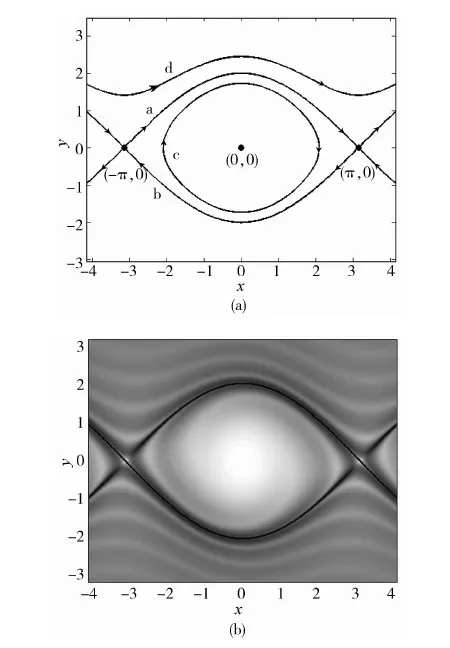
图1 单摆系统的相空间及其FTLE域(T=10)

在考查的定义域内取格点划分为300×300，T=10.对每一格点计算Lyapunov指数，并在图1(b)中以等高图绘出FTLE域.在图中可以清晰地看出脊线结构，即LCS，它们是趋近于两个鞍点的稳定流形.类似地，当取T=-10，我们可以得到不稳定流形.

3 时间周期不变流形的性质

在PCR3BP模型下，Koon等人[2]的研究表明，共线平动点附近的不变流形管作为轨道的不变集，是穿越轨道与非穿越轨道的分界面.本节将通过数值方法验证，ER3BP模型下的时间周期不变流形依然具有上述性质.

下面的数值仿真研究基于系统参数μ=0.1和e=0.2.

3.1 时间周期不变流形是运动分界面

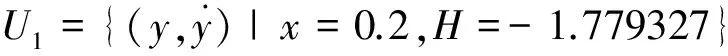
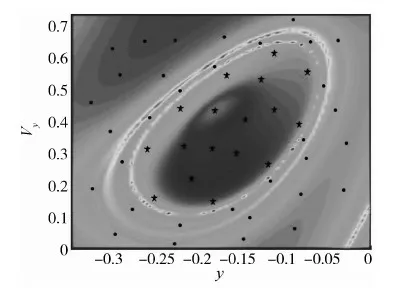
图2 U1截面处的FTLE域(T=2,f=π/2)

从上图中可以清楚地看到一条封闭脊线，即LCS，这是时间周期不变流形在U1截面上的截交线.如图所示，在该截线附近随机布置试验点阵.其中，位于不变流形截线外部的点以实心圆点表示，以其为初状态的轨道示于图3(a)；位于不变流形截线内部的点以五角星符号表示，相应的轨道示于图3(b).

从图3(a)和图3(b)中易见，由不变流形截线外部出发的轨道在M1-M2系L1点区域附近折返回M1，而由截线内部出发的轨道穿越了L1平动点区域，达到了M2附近.这说明，时间周期不变流形依然是穿越轨道与非穿越轨道的分界面.

3.2 时间周期不变流形是轨道不变集

在使用流形生长法对PCR3BP中的不变流形(以稳定流形为例)进行计算时，由Lyapunov轨道上沿稳定流形方向的微小偏移点出发，反向积分得到一条位于稳定流形上的轨道.实际上，这种处理本身已经蕴含了不变流形是轨道不变集的结论.

对于时间周期不变流形，由于难以直观地表达其整体形状，为了证明类似的结论，本文将采用一系列Poincare截面进行采样.

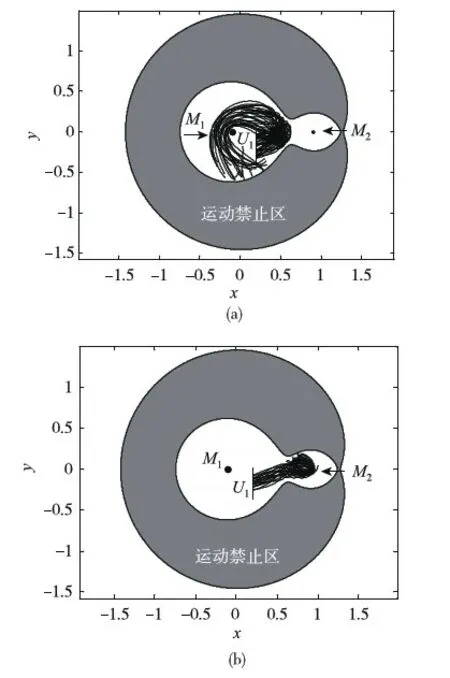
图3 非穿越轨道和穿越轨道

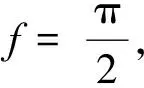
该典型轨道进入M1-M2系平动点区域，并表现出渐近收敛于准周期轨道的趋势.考察该轨道与截面x=0.3、x=0.4和x=0.5的截交，以截交点处的轨道能量确定出相应的Poincare截面：

(10)

(11)

(12)

在对应的真近点角下，各截面上的FTLE域等高图及该轨道在各截面的截交点绘于图5(a)～(c)中.

由图5(a)～(c)可以看到，在各截面上，轨道的交点恰好处于相应的LCS上.这反映出，该条轨道恰好落在时间周期不变流形上，从而表明时间周期不变流形是轨道的不变集.

图4 U1截面处的FTLE域(T=2,f=π/2)以及一条典型轨道

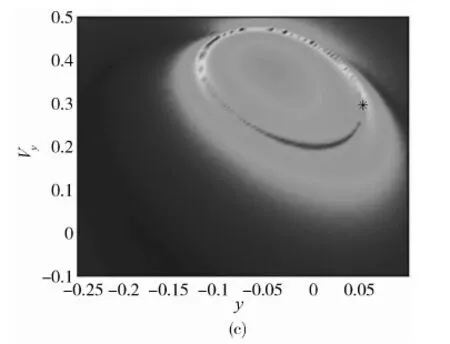
图5 U2、U3和U4截面处的FTLE域

4 结 论

本文对于椭圆三体模型中的时间周期不变流形得到了如下结论：

(1)时间周期不变流形是穿越轨道与非穿越轨道的分界面；

(2)时间周期不变流形是轨道不变集；

本文中利用LCS研究时间周期不变流形的方法可以推广到对时间任意依赖的动力系统中.

参 考 文 献

[1]Qi R, Xu S J, Xu M. Impulsive control for formation flight about libration points[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(2): 484-496

[2]Koon W S, Lo M W, Marsden J E, Ross S D. Heteroclinic connections between periodic orbits and resonance transitions in celestial mechanics[J]. Chaos, 2000, 10: 427-469

[3]Parker T S, Chua L O. Practical numerical algorithms for chaotic systems[M]. New York: Springer-Verleg, 1989

[4]Shadden S C, Lekien F, Marsden J E. Definition and properties of Lagrangian coherent structures from finite-time Lyapunov exponents in two-dimensional aperiodic flows[J]. Physica D, 2005, 212: 271-304

[5]Haller G. Distinguished material surfaces and coherent structures in three-dimensional fluid flows[J]. Physica D, 2001, 149: 248-277

[6]Gawlik E S, Du Toit P C, Campagnola S, et al. Lagrangian coherent structures in the planar elliptic restricted three-body problem[J]. Celestial Mechanics and Dynamical Astronomy, 2009, 103: 227-249

[7]Qi R, Xu S J, Zhang Y, Wang Y. Earth-to-moon low energy transfer using time-dependent invariant manifolds [C]. AIAA/AAS Astrodynamics Specialist Conference, Minneapolis, Minnesota， August 13-16, 2012

[8]Szebehely V G. Theory of orbits: the restricted problem of three bodies[M]. New York: Academic Press, 1967