基于线性协方差分析的接近天体在轨导航方法研究*

徐 超，黄翔宇，王大轶

(1.北京控制工程研究所，北京 100190；2.空间智能控制技术重点实验室，北京 100190)

对于接近深空天体的探测任务，探测器的飞行距离远、运行时间长、环境未知性较大，其导航和控制系统在实时性、精度和可靠性方面的要求更高.传统的基于地面测控网的导航与控制方法受到精度、传输时间、运行成本和可观测弧段等方面的限制，往往难以满足任务需要[1].

目前采用的接近段导航方式主要有两类：一类是结合地面无线电测量与光学成像测量的地面组合导航方式[2-3]；另一类是单纯依靠导航相机进行的光学自主导航.光学自主导航完全依赖于探测器上光学敏感器提供的观测信息，由于受光学敏感器精度、视场和目标天体光照等条件的限制，很难满足探测器对精度和可靠性的要求.融合光学信息和无线电信息的地面组合导航方式虽然满足探测器对导航精度和可靠性的要求，但其需要将光学测量信息传回地面站，再将地面站计算得到的导航信息返回探测器，这样无法满足实时性的要求.因此，为充分发挥光学和无线电导航的优势，有必要研究在轨融合光学信息和无线电信息的自主导航方法，从而提高在轨导航的精度和可靠性[4].

由于光学成像测量可以获得多种观测信息[5]，为选择合适的光学观测信息和无线电信息在轨融合，本文以火星接近段为背景结合线性协方差分析方法和基于B平面参数的误差分析方法，分析了不同光学观测信息和无线电测量信息在轨融合的自主导航方案.首先，介绍了标准的线性协方差分析方法；然后给出了接近段基于光学和无线电的导航测量模型，并给出了基于这两种测量的自主导航方案；其次，引入了B平面点位误差椭圆描述导航误差的置信度；最后，利用基于线性协方差分析的B平面参数误差分析方法对给出的自主导航方案进行了仿真分析.

1 线性协方差分析方法

线性协方差分析方法是由Geller和Stastny提出的一种新的导航控制误差分析工具，该方法只需要运行一次即可获得与蒙特卡罗仿真相似的结果从而大大节省仿真时间[6-7].

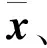
利用蒙特卡罗仿真进行导航误差分析是通过对N次仿真试验结果进行统计分析，从而得到导航误差的统计信息.真实状态偏差协方差阵Dtrue、导航状态偏差协方差阵Dnav和导航误差协方差Ptrue的计算公式分别为

(1)

假设导航系统真实状态模型为

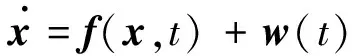
(2)

其中，w(t)为零均值的高斯白噪声序列，噪声方差为E(w(t)wT(t′))=Q(t)δ(t-t′)，Q(t)为噪声方差阵，δ(t-t′)为Dirac-δ函数.导航敏感器在tk时刻得到观测量为

zk=h(xk,tk)+vk

(3)

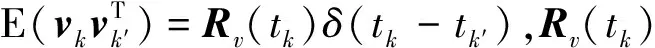
图1 状态描述

(4)

(5)

(6)

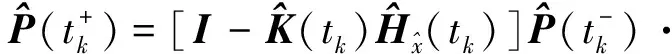
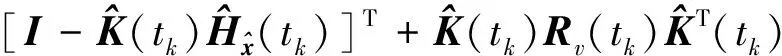
(7)

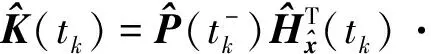
(8)

(9)

(10)

由于系统真实状态偏差δx(t)不受测量更新影响，故有

(11)

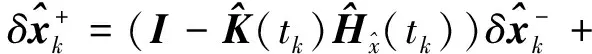
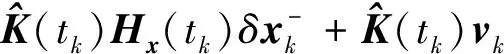
(12)

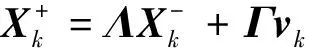
(13)

取扩展状态协方差为Θ=E(XXT)，则有

(14)

(15)

则式中各协方差阵可按下式计算:

Dtrue=E(δx(t)(δx(t))T)

=[In×n0n×n]Θ[In×n0n×n]T

=[0n×nIn×n]Θ[0n×nIn×n]T

=[In×n-In×n]Θ[In×n-In×n]T

综上，式(8)、(14)、(15)即组成线性协方差分析方法的协方差时间和测量更新方程.可看出利用线性协方差分析方法只需运行一次即可得到与蒙特卡罗仿真相似的导航性能分析结果.

对于导航问题，因为在仿真中探测器实际轨道作为已知量，因此可认为实际轨道和标称轨道相同，则上述求导航误差协方差阵的过程[8]可简化为

其中，

(17)

2 接近段导航测量

接近目标天体段，导航系统主要以目标天体为观测对象，通过导航相机获取包含背景恒星的目标天体光学图像，经过图像处理后得到天体视半径、天体中心点以及恒星点像素信息.同时通过在探测器上安装的接收机接收地面站发射的无线电导航信息，在轨获取探测器与地面站间的距离和径向速度等观测量.

2.1 基于光学信息的测量

2.1.1 目标天体中心像素信息测量

由光学导航原理可得，目标天体中心点像素的观测模型为

(18)

其中Cij(i=1,2,3;j=1,2,3)为目标天体J2000惯性坐标系到相机坐标系的方向余弦矩阵CcI中对应的元素，由姿态敏感器给出；[x,y,z]T为探测器在目标天体J2000惯性坐标系中位置；f为导航相机焦距；kx、ky为由毫米转换为像素的参数；p0、l0为导航敏感器中心像元和像线；vp、vl为观测噪声.

2.1.2 星光角距测量

通过目标天体中心点像素和多个恒星点像素信息可获得多个星光角距信息.星光角距测量是对目标天体与恒星视线夹角的测量，其观测模型为

ψsk=arccos

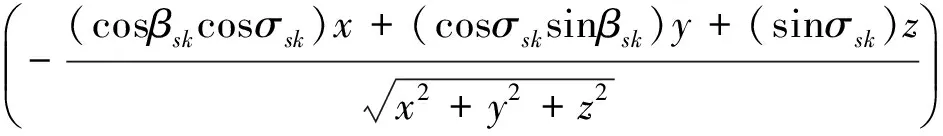
(19)

其中，(x,y,z)为探测器在目标天体J2000惯性系下位置，βsk,σsk为识别的第k颗恒星的赤经和赤纬，k=1,2,…,n，n为识别的恒星数，本文相关方案中取n=4.

2.1.3 目标天体视半径测量

通过对导航相机拍摄的目标天体图像进行处理可得到目标天体的视半径信息，其观测模型为

(20)

其中，R为目标天体参考半径，r为探测器相对目标天体中心的距离.

2.2 基于无线电信息的测量

无线电导航信息通常包含多普勒信息和距离测量信息，多普勒观测得到的是探测器与地面站之间的相对速度vr，距离测量得到的是探测器与地面站之间的距离rr.通过在探测器上安装接收机，在一定条件下探测器可接收到地面站发送的无线电信息，因此，可在轨获取探测器与地面站间的距离和径向速度信息，其观测模型为

(21)

其中

(22)

3 接近段自主导航方案

接近段自主导航系统以探测器在目标天体惯性系中的位置和速度为状态量，状态方程依据接近段轨道动力学模型建立，导航滤波算法采用扩展卡尔曼滤波.针对前述几种观测模型，给出下述6种导航方案，其中hi(i=1,2,…，6)为第i种方案对应观测量.

3.1 基于无线电测量的自主导航方案

探测器在轨接收地面站发射的无线电信息，可获取的信息主要包括探测器相对地面站的径向速度和距离信息，则基于无线电的在轨导航方案观测方程为

(23)

其中rr、vr如式(21)所示，分别为探测器相对地面站的距离和径向速度.

3.2 基于光学测量的自主导航方案

为充分利用光学导航图像获取的信息进行高精度导航，光学导航方案里应同时包含方向和距离信息，因此对上述3种光学观测量进行组合可有以下2种组合导航方式：

(24)

其中，p、l、ρ如式(18)、(20)所示，分别为目标天体中心像元、像线及目标天体视半径，ψs=[ψs1ψs2…ψsn]T为观测到的n个星光角距信息.

对于这两种基于光学测量组合的导航方案，前一种方案由观测模型可看出其需要探测器的姿态信息和敏感器的安装信息，因此其导航精度受姿态误差和敏感器安装误差的影响；而后一种方案虽也是由目标天体和恒星点像素信息得到，但在计算夹角信息时姿态误差和安装误差引起的测量误差被抵消，因此该方案不受这些因素的影响.

3.3 融合光学和无线电信息的导航方案

根据前述给出的光学导航方案，给出如下3种融合无线电和光学观测信息的在轨导航方案：

(25)

4 接近段导航B平面参数误差分析

由于建立在目标天体B平面上的参数与探测器轨道状态参数之间存在较好的线性关系，又可用来描述探测器目标轨道的散布，因此B平面参数除了可用于深空探测的轨道设计和控制外，还可用于深空接近任务段导航性能的评估.

图2 B平面及其误差椭圆

如图2所示，B平面一般定义为过目标天体中心并垂直于进入轨道的双曲线渐近线的平面.B平面坐标系定义为，以目标天体中心为原点，S轴为进入轨道渐近线方向，M为参考方向，此处取为目标天体赤道面法线方向，S与M的矢量积为T轴，R轴由S轴和T轴按右手法则确定，B矢量定义为由B平面原点指向双曲线轨道渐近线与B平面交点的矢量，记为B，其大小为双曲线短半轴长度，B平面参数BT和BR定义为B在T轴和R轴上的分量，即

BT=B·T,

BR=B·R

(26)

B平面靶点的导航不确定性可利用误差椭圆表达，有关B平面参数和误差椭圆的详细内容可参考文献[9-10].因线性协方差分析方法可获得与蒙特卡罗仿真相似的状态误差分布，因此可利用线性协方差分析方法确定的导航误差协方差阵确定B平面误差椭圆.

利用线性协方差分析方法可得到探测器在导航结束时刻tf的导航误差协方差Pf(x).由于B平面参数与探测器轨道状态参数之间有较好的线性关系，即ΔB=KΔx，其中ΔB=[ΔBTΔBR]，故有

PB=KPf(x)KT

(27)

其中K为B平面参数敏感矩阵，可通过数值方法求解，PB为B平面参数误差协方差阵.令σT、σR分别为BT、BR的误差标准差，ρRT为相关系数，则PB也可写为

(28)

对于实对称矩阵PB有

P′=UTPBU

(29)

式中，P′是以PB特征值λ1、λ2为主对角线元素的对角阵，U是由对应特征向量的标准正交基构成的矩阵.令[x′y′]T=UTΔB则有B平面误差椭圆方程如下：

(30)

当L分别取1、2、3时，得到椭圆分别为1σ、2σ、3σ误差椭圆.设λ1≥λ2，则误差椭圆长短半轴及方向角可计算如下:

(31)

式中Ui1(i=1,2)为U中对应元素.

接近天体点高度标准差可计算为

(32)

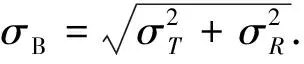
5 仿真分析

以接近火星探测任务为例，针对给出的6种接近天体在轨导航方案和基于线性协方差分析的B平面参数误差分析方法进行数学仿真.

5.1 仿真条件

1)标称轨道由STK生成，考虑火星80×80阶引力场、太阳引力、火卫星引力和太阳光压摄动；仿真采用简化动力学模型，只考虑太阳引力摄动和火星非球形J2项摄动，取系统模型误差方差阵为

Q=diag{0,0,0,10-5,10-5,10-5}

2)探测器在火星J2000惯性系下初始位置、速度：

X0=[227326.99km;-160020.36km;

126502.87km;-2.58386631km/s;

1.8939265km/s;-1.5008243km/s]

3)导航初始误差：位置各方向为100km，速度各方向10m/s.

4)观测误差：无线电距离测量误差100m(1σ)；无线电径向速度测量误差0.1m/s(1σ)；光学敏感器焦距677mm，光学观测误差0.1像素(1σ)，光学角度测量误差0.01°(1σ).

5)姿态误差各轴方向5″(1σ).

6)滤波方法EKF，滤波周期30s，导航仿真时间20h.

5.2 仿真结果及分析

图3、4分别给出了方案4由线性协方差分析方法和蒙特卡罗仿真得到的导航误差分布和B平面参数误差分布结果.图3中虚线为由线性协方差分析方法得到的状态误差标准差包络线，实线为200次蒙特卡罗仿真结果，图4中3个椭圆是由线性协方差分析方法得到的对应1σ、2σ、3σ的B平面误差椭圆，小圆圈代表1000次蒙特卡罗仿真得到的B平面打靶结果，由仿真结果可看出线性协方差分析方法得到结果与蒙特卡罗仿真结果基本一致.表1给出了无线电导航、光学导航及融合无线电和光学信息的导航方案B平面参数精度对比.图5给出了不同导航方案的B平面误差椭圆，图6比较了不同姿态误差下方案4的B平面误差椭圆与方案5的B平面误差椭圆.

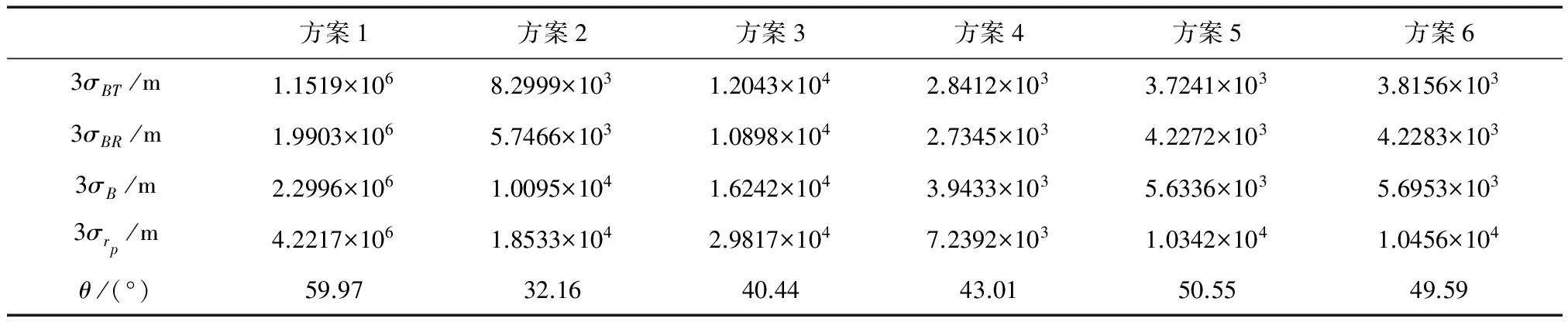
表1 不同导航方案对应的B平面参数误差

由仿真结果可看出，光学导航精度远优于无线电导航，融合光学信息和无线电信息的导航方案精度高于光学或无线电信息单独进行导航的精度；当姿态误差较小时，基于火心像素和火星视半径信息的光学导航方式优于基于星光角距和火星视半径信息的光学导航，相应的融合无线电信息后的导航精度前者也优于后者，但随着姿态误差增大，融合无线电、星光角距和火星视半径信息的导航方式精度逐渐高于融合无线电、火心像素和火星视半径信息的导航方式精度，见图6，这是由于火心像素观测信息对姿态误差极其敏感，而基于星光角距和火星视半径信息的光学导航不受姿态误差的影响，与前面分析一致；由图5的结果可看出方案5比方案6的精度稍高但并不明显，这主要是因为火星视半径信息在距火星较远时对探测器状态变化不敏感所致.

图3 线性协方差与蒙特卡罗仿真结果比较

因此当探测器姿态误差较小时，应以目标天体中心像素为主要的光学观测信息，当姿态误差较大时，则应以星光角距为主要的光学观测信息；当距离目标天体较近时，可增加目标天体视半径为主要光学观测信息.

图4 方案4的B平面误差椭圆和蒙特卡罗打靶结果

图5 不同导航方案的B平面误差椭圆

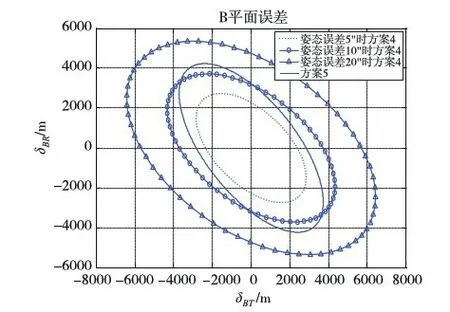
图6 在不同姿态误差下方案4与方案5 B平面误差椭圆比较

6 结 论

本文结合线性协方差分析方法和基于B平面参数的误差分析方法，分析了在轨融合无线电测量信息和光学观测信息的自主导航方法.由线性协方差分析得到的B平面参数误差表明，在轨融合无线电测量信息和光学观测信息的导航方法可有效提高预测的B平面参数和目标天体近心距精度；在考虑姿态误差影响时，选择合适的光学观测信息和无线电测量信息进行融合可提高系统导航精度和可靠性.

参 考 文 献

[1]王大轶,黄翔宇.深空探测自主导航与控制技术综述[J].空间控制技术与应用,2009,35(3):6-12

Wang D Y, Huang X Y. Survey of autonomous navigation and control for deep space exploration[J]. Aerospace Control and Application, 2009, 35(3):6-12

[2]Bhaskaran S, Riedel J E, Synnott S P, et al. The deep space 1 autonomous navigation system: a post-flight analysis[C]. AIAA/AAS Astrodynamics Specialist Conference, Denver, CO, USA, Aug 2000

[3]Ryne M, Jefferson D, Craig D, et al. Ground-based orbit determination for deep impact[C]. The 16thAnnual AAS/AIAA Space Flight Mechanics Meeting, San Diego, CA, 2006

[4]黄翔宇,王大轶.基于光学和无线电信息的接近天体在轨导航方法研究[C].全国第十五届空间及运动体控制技术学术会议,长春,2012

Huang X Y, Wang D Y. Study on autonomous navigation based on optical and radio measurements for the approach phase of interplanetary mission[C]. The 15thAcademic Conference on Space and Movement Body Control Technology, Changchun, 2012

[5]黄翔宇.深空自主导航系统的可观性分析[J].宇航学报,2006,27(3):332-337

Huang X Y. Observability analysis of deep space autonomous navigation system[J]. Journal of Astronautics, 2006, 27(3): 332-337

[6]Geller D K, Rose M B, Woffinden D C. Event triggers in linear covariance analysis with applications to orbital rendezvous[J]. Journal of Guidance Control and Dynamics, 2009, 32(1): 102-111

[7]Geller D K. Linear covariance techniques for orbital rendezvous analysis and autonomous onboard mission planning[J]. Journal of Guidance Control and Dynamics, 2006, 29(6): 1404-1414

[8]Stastny N B, Geller D K. Autonomous optical navigation at Jupiter: a linear covariance analysis[J]. Journal of Spacecraft and Rockets, 2008, 45(2): 290-298

[9]Kizner W. A method of describing miss distances for lunar and interplanetary trajectories [R]. NASA CR-63483, 1959

[10]Byron D T, Bob E S, George H B. Statistical orbit determination[M]. USA: Elsevier Academic Press, 2004, 251-261