基于Tersoff-Brenner势的航天器群图形编队研究*

曾志峰，汤一华，陈士橹，徐 敏

(1.西北工业大学航天学院,西安710072; 2.航天飞行动力学技术重点实验室,西安710072)

随着MEMS(微机电系统)技术的发展[1], 人们把更多目光投向了微小型航天器.通过近年迅猛发展，微小型航天器已然成为大型航天器的一个有力补充.相对大型航天器，微小型航天器虽结构简单、功能较单一，但其集群可在一定群控制律下虚拟成一大型航天器，从而实现甚至超越大型航天器的功用，其优点可以归结为以下几点：1)结构简单，2)鲁棒性高，3)任务适应性、拓展性强，4)经济.

一般地，航天器群任务可分为以下两种，即图形编队任务和协同任务.前者主要通过相应群控技术将群编成静态或动态(相对于轨道坐标系)目标构型，群体有序性体现在几何构型的层次；而后者，群体有序性体现在任务实施的层次，诸如协同搜救和协同攻击等任务，其几何构型不固定随时可能发生变化.基于图形编队的基础、重要性，本文着重于此展开研究.在此领域，Izzo基于人工势场法(APF, artificial potential field)开发了一名为速度平衡塑形技术(equilibrium shaping approach)的方法[2].此法能使群体成员仅在局部感知信息下自组织地编成目标空间构型，但由于此法利用几何对称性来消减方程数量求解人工势场参数，故而只能编制特定几何对称性的构型.文献[3]中，Derek采用分叉理论[4]设计全局势场，仿真结果显示，采用音叉式分叉场(pitchfork bifurcation)，群体成员可自发编成单圆、双圆及圆面均布构型，且通过更改几个分叉场参数，便可在构型间切换.与上两方法中采用简单成对指数函数构建局部势场用以避免成员相撞不同，Pinciroli等人[5]利用著名分子间相互作用力经验模型伦纳德-琼斯势[6](LJP, Lennard-Jones potential)构造局部势场，使成员在避撞同时编制成正六边形局部构型(带中心)，构型中相邻成员间距几乎一直(值为预先设定)，美中不足的是整个构型的外围形状不能精确地表现，成员较少的情况下尤是.对于以上方法，中国也进行了相关的研究，但从可以获得的文献看，大多集中在机器人编队领域，而航天领域尚处在技术移植阶段，相关文献较少.姚红、汤亚锋把常规的人工势场法扩展应用于航天器编队的协同控制[7]，指出基于人工势场法的协同控制算法计算量较小,适于多智能体的实时协同控制；分叉势场法和伦纳德-琼斯势法则尚未发现相关文献.

通过分析可知，以上各个方法均有各自的优缺点和适用范围，从本质上讲均属于人工势场法范畴，不同之处在于所用势场的类型、脚本、稳定收敛的方法以及目标构型的特点.相比之下，本文尤其关注Pinciroli C文献[5]，从中能够看到从分子动力学模拟角度进行群控研究的可能.与Pinciroli C文献不同，鉴于碳氢分子，尤其是碳元素同素异形体(诸如石墨、金刚石、石墨烯、碳纳米管及其它富勒烯)结构的优良特性(作者认为其定将在未来航天群任务中有着广阔的应用前景)，以及考虑到Tersoff-Brenner经验势模型在以上结构分子动力学模拟中的成功应用，首先将以该势模型为基础，开发出一种新颖的图形编队方法，其次通过实例仿真，验证该法在航天器群任务中的可行性，最后对该法进行总结并对其发展做一些前瞻性探究.

1 方法介绍

与文献[5]方法类似，编队过程中，成员期望控制加速度矢量u也由三部分构成，即u=g+l+d，其中g为汇聚势场加速度矢量，l为局部势场加速度矢量，d为耗散加速度矢量(为叙述方便，文中g、l等亦指相应人工势场).航天任务中，为减少能耗，可利用万有引力来汇聚成员，与文献[2]类似，将g分成两部分：远端汇聚场gfar及近端汇聚场gnear.gfar基于C-W方程[8]改造而来，自编队过程开始绝大部分时间内成员受此势场驱动，向目标构型中心汇聚；不过由于gfar临近构型中心时，会因系数阵奇异导致失效，此时成员将在近端汇聚场gnear导引下进一步向构型中心汇聚.除汇聚场g外，局部塑形场l基于Tersoff-Brenner势构建，耗散项d采用文献[5]形式.

在介绍以上各项具体形式前，先简介本文方法运行脚本.以目标构型中心为汇聚中心，可将其周边区域粗分为两大部分：远程段和近程段.远程段占编队空域绝大部分，其间成员以极小能耗自初始位置汇聚到目标构型周边，期间避免碰撞，藉此目的，此段势场由gfar及l构成.相应地，近程段目的在于进一步汇聚成员、避碰、编制目标构型并确保过程稳定收敛，故而此段势场由gnear和l组成，成员兼受耗散项d作用，并在三者共同作用下，最终自发完成图形编队任务.

以下介绍各人工势场及耗散项构造，假定成员均知道参考坐标系o-xyz下各自位置矢量r和速度矢量v.

1.1 全局汇聚势场

1)远端汇聚场gfar：设置与文献[2]类似，与之不同的是，本文建立的是力势场，不是文献[2]中的速度势场，故而文中gfar值实为基于C-W方程推导所得期望速度融合控制律所得出的控制加速度值，简要推导整理如下：

(1)

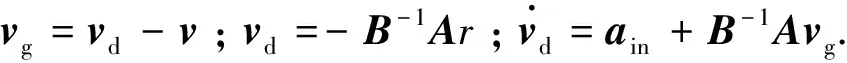
gfar=(kI+B-1A)vg

(2)

式中：k为一正实数，仿真中适当选定；ain为航天器成员由惯性力在参考坐标系中产生的加速度矢量；I为3×3单位矢量；系数矩阵A，B-1的具体形式参见文献[9].

2)近端汇聚场gnear：鉴于矩阵B-1在临近目标点时会出现奇异，为继续汇聚成员，将利用Morse势[10]构造近端汇聚场gnear以替代gfar.先介绍起纯汇聚作用的基本势场gfree，假定汇聚目标点为r0=[x0y0z0](一般为参考系o-xyz原点)，则当前位置r的成员所受该势场引起的加速度为

gfree=αf(r0-r)e-(r0-r)2/kf

(3)

式中：αf为增益参数；kf为作用范围参数.当对构型朝向相位有要求时，可在gfree基础上附加或直接替换为驻留势场gdock.通过驻留个别成员来达到朝向相位要求.gdock形式与gfree相同，r0为所选驻留点位置，增益和作用范围参数分别为αd、kd.

1.2 局部塑形场

本文采用Tersoff-Brenner经验势[11]构建的局部塑形势场，避撞的同时使临近成员编成局布构型.Tersoff-Brenner势是一种半经验多体势模型，广泛用于碳氢分子的分子动力学模拟，模拟碳碳原子间、碳氢原子间化学键作用.虽因高精度较同类型势场模型复杂，但因模型中函数均属短程函数，结果能迅速算出，故而在碳碳及碳氢系统的计算机模拟中发挥着举足轻重的作用.以下介绍Tersoff-Brenner势的具体形式.

系统中i原子的总势矢量Ei可以表示为：

(4)

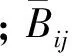
(5)

(6)

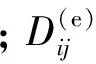
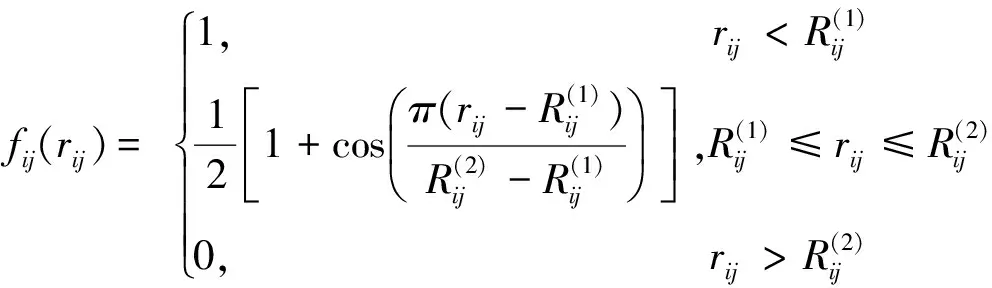
(7)

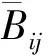
(8)

式中：

(9)

(10)

Gi(θijk)为原子i-j和i-k化学键键角函数.

通过对Ei求ri的偏导数就可以得到i原子所受其他原子的作用合力Fi，即

(11)

式中：n为原子数目.由于篇幅有限，偏导数具体形式请参见文献[12].为将Tersoff-Brermer势成功移植到航天器群任务中，将进行以下两个处理： 其一，为计算简便，常把系统的单位归一化，使R(e)等于1，作为对应，航天应用中，航天器间距值为同单位制下实际间距除以期望间距所得商；其二，引入常量μ，用以调配原子键间力量级与实际航天器动力量级之间的差别，如此之后，对于群体中的第i个成员，局部塑形势场引起的加速度矢量li可表达为：

li=μ(Fi/ms)

(12)

式中：ms为碳原子质量.方程(5)～(12)中其他参数参见文献[11].

1.3 耗散项

以上汇聚势场g和局部势场l本质上属保守势场，需引入耗散项耗散虚拟能量以确保编队收敛，这里耗散项d采用文献[5]形式，具体表达式如下：

d=-ξv

(13)

式中：ξ为耗散系数.

2 仿 真

为验证方法的有效性，作为先期研究，本文以金刚石结构单元带心正四面体为航天器群图形编队任务的目标构型，如图1限定朝向和相位.鉴于地球同步轨道(GEO)的巨大应用价值，本文将其作为参考轨道，当然本文方法也同样适用于其他行星中心开普勒轨道.

首先，在GEO上建立参考坐标系o-xyz(即轨道坐标系，见图1)，其中原点o为目标构型中心点，x轴为地心原点连线，背离地心方向；z轴与GEO轨道角动量方向保持一致，y轴与x、z轴相互垂直，三者满足右手定则.

其次，依照方法介绍部分介绍，通过设置以目标构型中心点为球心的外、中、内三个球面(见图1，其中router≫rmiddle>rinner)，将目标构型中心点周边空域由外到内进一步分为以下三个区域：

(1)借力汇聚层

范围从各航天器成员初始化(o-xyz下零初速)的外球面到gfar势场内边界.域内gfar为主要势场函数，航天器主要借助万有引力飞行.需要说明的是，gfar势场的内界包含两个：其一为中球面，用以标定gfar的空间最大延伸范围；其二为时间边界tnatural，用以标定gfar的最长作用时间.

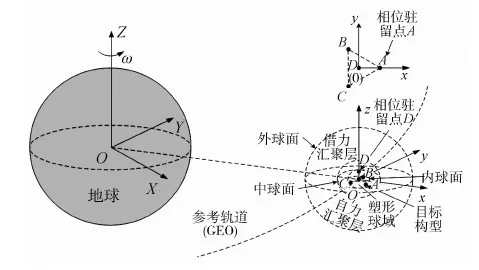
图1 仿真示意图(黑点代表目标构型，右上角视图为目标构型在xy面上投影，D、O、A分别为所选朝向与相位驻留点.)

(2)自力汇聚层

范围由gfar势场的内边界到内球面，gnear代替gfar继续汇聚成员，航天器轨迹不再是万有引力下的自然飞行轨道.

(3)塑形球域

即内球域，目标是在gnear汇聚控向基础上，通过局部塑形势场l使成员自动编制构型，并通过耗散项d确保编队过程稳定收敛.当目标构型有朝向相位要求时，可依构型特点启用gdock.

编队过程中以上三球层域全程施加局部塑形势场l避撞，耗散项d仅后两层域施加，保证快速性.

再其次，本文假定在参考系o-xyz下，各成员除知道自身位置及速度外，还可通过在轨测量或是局部通信等手段获知自身感知球(球径rsensor)内其它成员的位置.发动机采用连续小推力式，加速度大小限幅umax.

最后设定仿真参数开始仿真，表1列出了仿真中所用参数，Tersoff-Brenner 模块参数参见文献[11]中表1.为方便及减少数值误差，仿真中各参量采用无量纲形式.其中航天动力学模块无量纲化因子分别为：地球质量、赤道半径、自转角速度；Tersoff-Brenner模块则为：碳原子质量、碳原子间平衡距离及势阱深度.

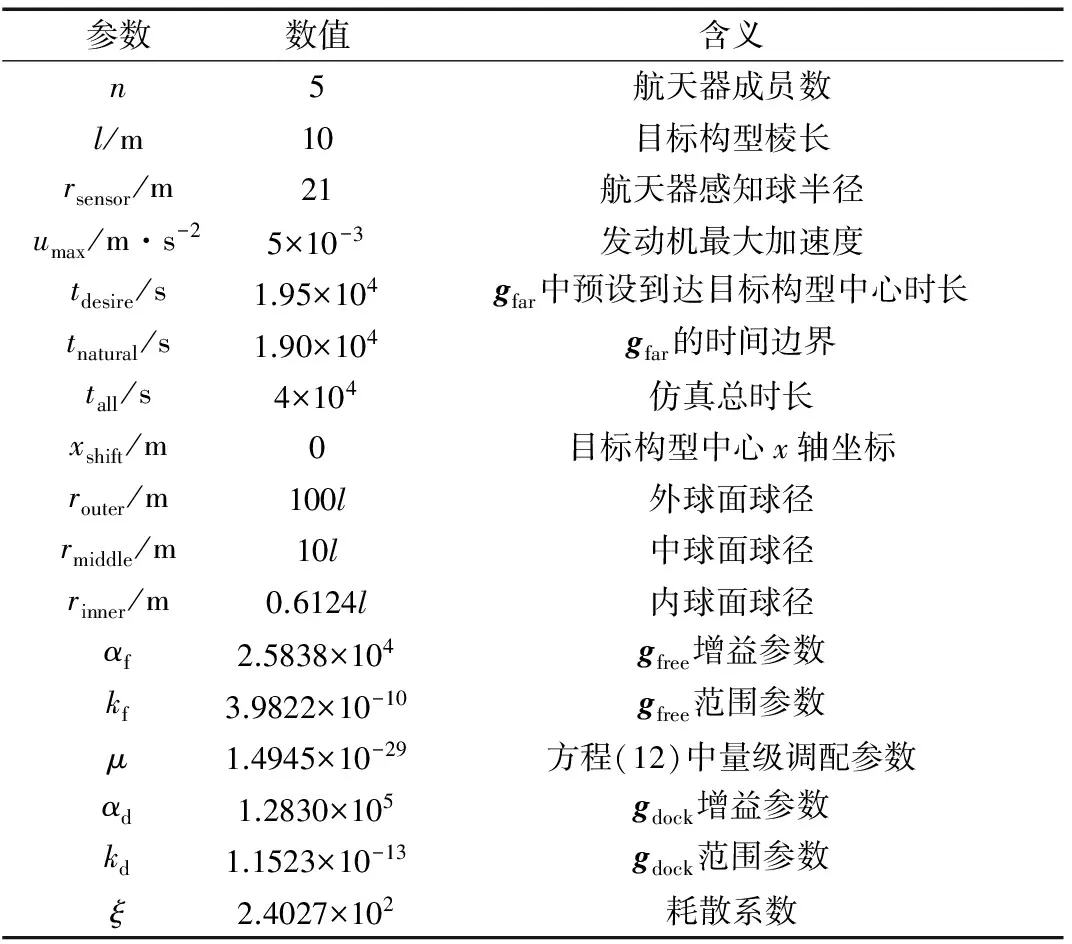
表1 仿真中所用参数

如上分析设置后，详细仿真结果及分析如下：

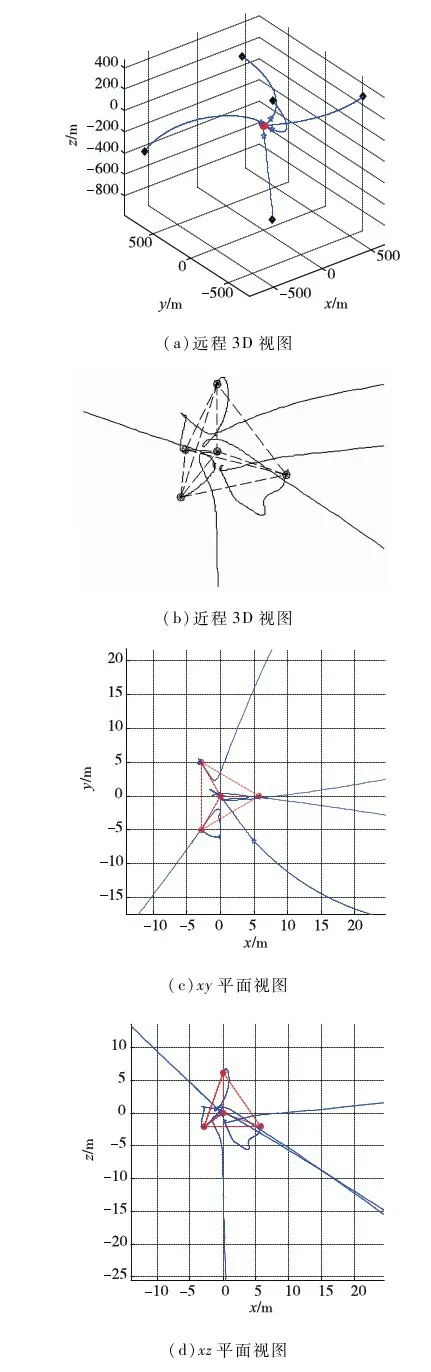
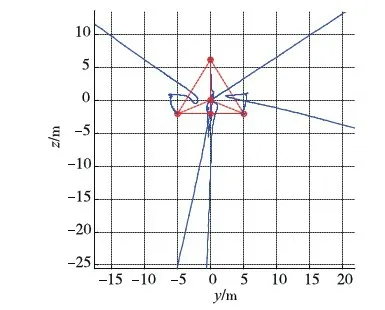
(e)yz平面视

如图2～4所示，仿真开始后不到20000s，航天器群便稳定收敛形成目标构型，中心成员位于参考系原点，朝向相位均满足要求，编队过程无成员碰撞.其中图2(a)主要显示航天器群在借力汇聚层的运行情形，此阶段汇聚势场为改造自C-W方程的gfar，航天器绝大部分时间在万有引力作用下“滑翔”运行，轨迹自然顺滑；图2(b)显示的是航天器群接近目标构型时(自力汇聚层及塑形球域)的汇聚塑形情形，该图显示在势场gnear、l及耗散项d共同作用下，成员能自组织地形成期望构型，轨迹较借力汇聚层轨迹更弯折；图2(c)～(e)依次描绘了成员终态构型在xy、xz及yz面上的投影.图3为成员速度视图，从零初速开始，在最初的约莫20s内，航天器速度在gfar作用下急剧升至“自然滑翔”轨道速度，此后成员循“滑翔”轨道滑向目标构型中心，直至约莫16880s左右gfar由gnear替代，经过一小段较大幅振荡后，在gnear、l及d联合作用下，各航天器逐步减速并近乎静止于各目标点附近，仿真结束时刻速度量级为10-5m/s.图4为各成员控制加速度图，由(a)、(b)两图可看出，整个编队过程中，能耗最大的地方主要有两处：其一就是编队开始的前约20s，发动机满偏，使成员迅速“爬”上“滑翔”轨道，其二就是在约16880s后，对应自力汇聚层和塑形球域，此时段航天器需克服万有引力，在gnear、l及d联合作用下使成员稳定收敛形成期望构型.整个编队仿真中，航天器最大速度小于0.46m/s，加速度均未超出发动机最大允许值，平均相对到位误差3.9932×10-4，即在本文仿真目标构型棱长为10m的情况下，各成员的平均到位误差仅不到4mm.

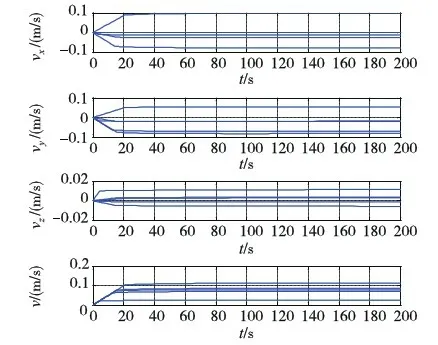
(a)前200s

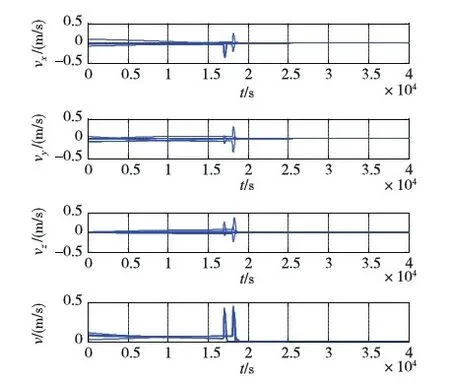
(b)仿真全程

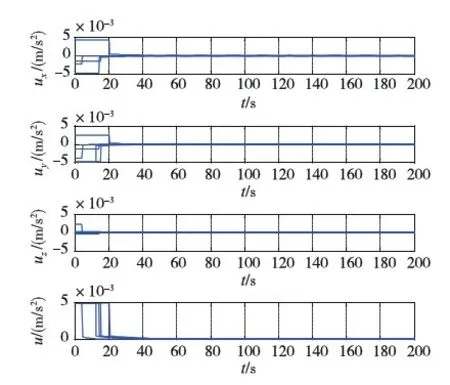
(a)前200s

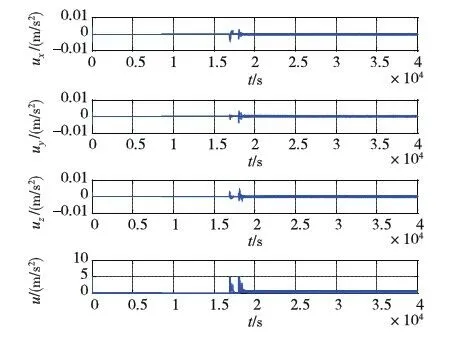
(b)仿真全程

需要说明的是，仿真中所用参数，尤其是势场参数的设置很关键，主要应满足两方面要求：其一为合理性要求，目的在于消除势场法固有的假平衡现象，其二为性能要求，目的为以最短时间最小能耗完成任务.因本文着重验证方法的可行性，为简便起见，仿真所用参数仅调整至合理值，故尔从图4b中依然可看出 后段依然有小的振荡(最大值为5.39×10-4m/s2).

由上可看出，本法能在避碰前提下自动导引航天器编成预定构型，且导引过程中各航天器仅需制导自身的位置速度，以及感应区内其它航天器的位置信息.值得说明的是，本方法同样适用于其它行星中心开普勒轨道的图形编队任务，仅需依照新的C-W方程推导出gfar置换即可.另外，方法中的目标构型除了金刚石结构单元体心正四面体之外，还可为其它基本构型和基于基本构型的组装构型.限于篇幅，仅以如下石墨结构单元正六边形为例说明.

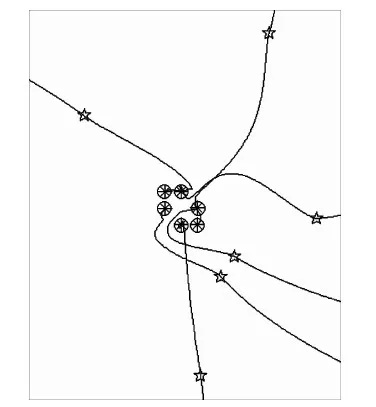
图5 正六边形构型仿真近程3D图(五角星：航天器到达gfar势场内边界时位置；圆：航天器最终稳定位置；星形：航天器目标构型位置；实线：航天器运行轨迹)

3 结束语

本文提出了一种基于Tersoff-Brenner势的自组织图形编队方法，适用于行星中心开普勒轨道上的航天器群图形编队任务.通过GEO上的该型任务仿真显示，航天器能在有限感知信息条件下，消耗少量的计算资源，自发地形成目标构型，且编队过程无碰撞.显然，此法亦可方便地移植到其它平台群任务中，诸如机器人、无人机、无人水下潜行器等.

验证完方法可行性，接下来的工作，一方面将重心放在大型拟碳氢分子空间结构的模拟上，如金刚石、石墨烯、碳纳米管、足球烯等空间结构，相信这些结构在空间任务中将发挥奇特功用；另一方面，结合分子动力学模拟最新技术成果，研究开发出基于其他势场模型的类分子结构的群控技术.通过以上努力拟将群控技术和分子动力学模拟技术二者结合起来，以期达到“分子构型打印机”的效果，为群控技术的发展提供一个全新的思路，即针对群任务，只需选取适合任务实现的分子构型，再基于分子构型的模拟势场，便可群控编队，完成任务.

参 考 文 献

[1]Osiander R, Darrin M G, Champion J L. MEMS and microstructures in aerospace application [M]. Florida: CRC Press, 2006

[2]Izzo D, Pettazzi L. Autonomous and distributed motion planning for satellite swarm [J]. Journal of guidance, control and dynamics, 2007, 30(2): 449-459

[3]Bennet D J, McInnes C R. Distributed control of multi-robot systems using bifurcating poten-tial fields [J]. Robotics and Autonomous Systems, 2010, 58: 256-264

[4]David Crawford J D. Introduction to bifurcation theory [J]. Rev. Mod. Phys., 1991, 63: 991-1037

[5]Pinciroli C, Birattari M, Tuci E, et al. Self-organizing and scalable shape formation for a swarm of pico satellites [R]. IRIDIA-Technical Report Series, Technical Report, No. TR/IRIDIA/2008-009, Bruxelles: IRIDIA, 2008

[6]Burkert U, Allinger N L. Molecular mechanics [M]. Washington D. C.: American Chemical Society, 1982

[7]姚红，汤亚锋.基于人工势场法的航天器编队协同控制 [C].中国智能自动化会议，南京，2009年9月27日

Yao H, Tang Y F. Coordinated control of spacecraft formation based on the artificial potential field [C]. Chinese Intelligent Automation Conference, Nanjing, September 27, 2009

[8]Clohessy W H, Wiltshire R S. Terminal guidance system for satellite rendezvous [J]. J. Aerospace Science, 1960, 27(9): 653-674

[9]McQuade F. Autonomous control for on-orbit assembly using artificial potential functions [D]. Glasgow: Faculty of Engineering, University of Glasgow, 1997

[10]McQuade F. Autonomous control for on-orbit assembly using artificial potential functions [D]. Glasgow: Faculty of Engineering, University of Glasgow, 1997: 89-90

[11]Brenner D W. Empirical potential for hydrocarbons for use in simulating the chemical vapor deposition of diamond films [J]. Phys Rev B, 1990, 42(15): 9458-9471

[12]何兰.微/纳米机电系统中的碳纳米管的机械性能研究 [D].西安: 西北工业大学,2004

He L. Research of the mechanical properties of carbon nanotubes in the micro/nano electrical and mechanical system [D]. Xi’an: Northwestern Polytechnical University, 2004