SDZ-8151挠性短节的动力学仿真设计及强度校核

孙 刚，张必波，郭振华

(中国电子科技集团公司第二十二研究所 河南 新乡 453003)

0 引 言

在复杂井况中，如果仪器串不能够弯曲或者弯曲不灵活，就会使仪器串在井中运行困难甚至发生卡滞遇阻，严重影响测井作业甚至发生测井事故[1]。原SDZ-8150挠性短节在使用过程中存在遇阻后被拉断的情况，在功能上已经不能很好地满足油田的测井需求。根据油田水平井测井需求，在长度、挠转角、拉伸强度以及抗扭强度等指标上对原挠性短节展开了重新设计和校核，形成了SDZ-8151挠性短节设计任务书。

根据设计任务书，初步完成了SDZ-8151挠性短节方案设计，采用动力学模型仿真分析了内径和挠性节间隙对挠转角度的影响，并以此为依据完成了挠转角设计；然后使用有限元的方法校核了挠性短节的强度，保证了SDZ-8151挠性短节的安全性和可靠性。

1 挠转角动力学仿真模型

为了得出挠性短节悬垂状态的挠转角，常采用估算挠转角的方法，其过程如下：通过PROE部件干涉分析，三维建模设计后进行挠度的测量。挠性节长度的最小化根据所需的挠度叠加挠性节的数量即可[2]。这种方法避免了建立复杂的约束方程，是利用三维软件建立实体模型后，不断地拖动挠性节使其发生边界干涉，然后估算两个挠性节轴线之间的夹角，再根据挠性节的数量乘以相应的倍数，这种方法更多地依赖于操作人员的经验，不能直观反映内径和挠性节间隙等因素对挠转角的影响。本文通过建立多组动力学模型，仿真分析了挠性节内径和挠性节间隙对挠转角的影响，根据仿真结果设计了挠转角。

为了更好地分析设计目标，将挠性短节简化为图1所示:从左到右的挠性节分别定义为A到E，挠性节E的轴线与x轴的夹角定义为挠转角α，在自然悬垂状态下α的值就是技术任务书对设计指标的要求。为了求α的值，选择在挠性节E的轴线及其延长线取两点G1和G2。事实上，在自然悬垂状态下挠性节E的轴线并不总在平面xoy，当G1G2为空间直线时，求x轴和空间直线G1G2方向向量的夹角值。

图1 挠性短节挠转角示意图

使用CAD软件建模，将相应的三维模型导入到机械系统动力学软件中，模拟挠性短节在重力下的自然悬垂状态。在模型左侧施加固定约束,通过软件材料工具库定义模型材料属性为金属。在常用的机械系统动力学软件中有两种计算接触力的方法，一种是补偿法(restitution);另一种是冲击函数法(impact)[3]。根据现有资料，金属之间的接触可以采用冲击法，在挠性节之间施加接触，系统的重力方向沿y轴负方向。

通常在机械系统动力学软件中 ,动力学仿真参数设置主要包括仿真输出步长和求解器的参数设置。仿真输出步长的参数设置主要通过仿真时间和步数来确定[4]。设置仿真时间time=5 s，仿真步数设置为step=5 000；然后挠性短节在重力的作用下，进入自然悬垂状态，如图2所示。

图2 挠性短节的悬垂仿真过程

通过标记点功能在挠性节E的中轴线上建立两个标记点G1和G2，仿真测量后得到G1和G2的坐标值,求出直线G1G2的方向向量，然后将G1G2的方向向量和x轴的方向向量Sx=(1,0,0)，带入空间直线夹角公式[5]，然后求两条直线的夹角α，可得：

(1)

2 挠转角的仿真设计

SDZ-8151挠性短节设计任务书要求如下：

仪器外径Φ89 mm；

拉断力不低于300 kN;

扭矩不低于800 N·m；

仪器长度不超过800 mm；

挠转角≥10°

根据设计任务书，将SDZ-8151挠性短节的外径尺设计为89 mm,将挠性节数量设计为5节，挠性节长度为482 mm,保证SDZ-8151挠性短节仪器的整体长度不超过800 mm。挠性节的间隙采用凸凹割线形式，在割线的拐角位置倒圆角，减小应力集中。在根据设计任务书完成了初步的方案设计以后，能影响挠转角的因素就只有内径d和挠性节间隙t,如图3所示。

图3 挠性短节方案示意图

挠性短节的内径可以从44 mm到69 mm变化，挠性节间隙可以从0.5 mm到3 mm取值，为了分析不同内径和挠性节间隙对挠转角度变化的影响，采用取值的方式建立了16个仿真模型，仿真计算不同模型下挠转角α的值，见表1。

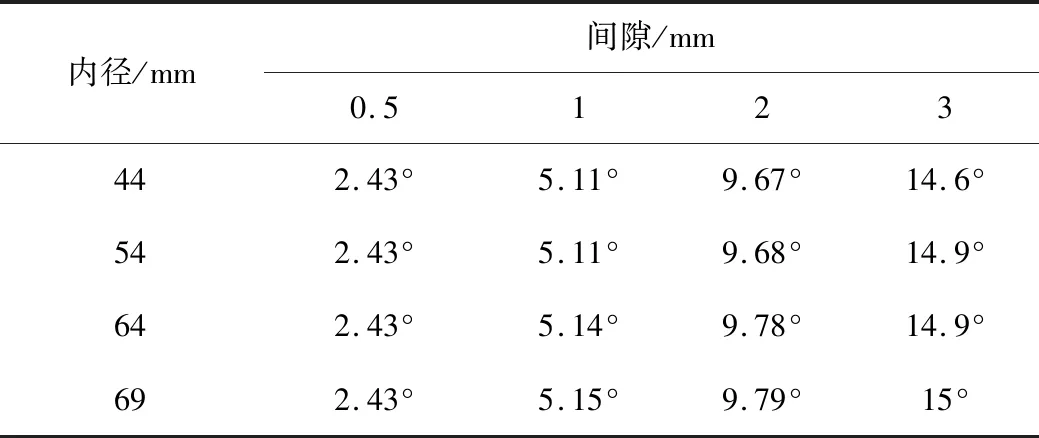
表1 不同内径和挠性节间隙时挠转角α的值

从仿真计算结果可见: 在挠性节间隙相同的情况下，内径对挠转角的影响不大;随着挠性节间隙的增大，挠转角也在增大，挠性节间隙是影响挠转角度变化的主要因素。因此，在设计挠转角时可以不考虑内径，内径可以根据实际需求来选取。当t=2 mm时，挠转角接近10°。根据任务书要求，取挠性节间隙t=2.2 mm，仿真计算挠性角是否满足设计要求。

建立挠性节间隙t=2.2 mm的模型，通过标记点功能在挠性节E的中轴线上建立两个标记点G1和G2，仿真计算后取其坐标，如图4所示。

图4 G1和G2标记点坐标值

取G1(369.8，-29.81,0.3229)和G2(480.5,-50.86,0.428)最终的坐标值, 可以计算直线G1G2方向向量SG1G2=(110.7，-21.05,0.17),x轴的方向向量Sx=(1,0,0)。

将直线G1G2方向向量SG1G2=(110.7，-21.05,0.17)和x轴的方向向量Sx=(1,0,0)，带入公式(1)，求两条直线的夹角α，可得：

通过上面的仿真计算可知，当取挠性节间隙t=2.2 mm时，挠转角α≥10°,满足设计要求。

3 挠性短节的强度校核

3.1 拉伸强度校核

在确定了挠性节的间隙以后，为了尽可能保证挠性短节的强度，内径取d=44 mm。首先校核挠性节的抗拉强度。取一段挠性节为研究对象，材料为05Cr17Ni4Cu4Nb，材料的σs=900 MPa,有限元模型用二阶四面体单元，单元类型为默认的solid187，单元大小5 mm; 施加300 kN的载荷，添加固定约束，建立有限元模型如图5示。

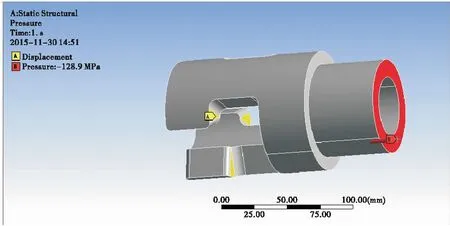
图5 拉伸状态有限元模型

经过计算，取Von-Mises应力云图，最大应力σmax=803.7 MPa，小于材料的屈服极限，可以判断在300 kN的拉力下,挠性节并未屈服，满足设计要求，如图6所示。

图6 拉伸强度的Von-Mises应力云图

3.2 抗扭转强度校核

在校核挠性节的抗扭转强度时，材料为05Cr17Ni4Cu4Nb，材料的σs=900 MPa,有限元模型用二阶四面体单元，单元类型为默认的solid187，单元大小5 mm，将载荷调整为800 N·m扭矩，并施加相应的边界约束，如图7所示。

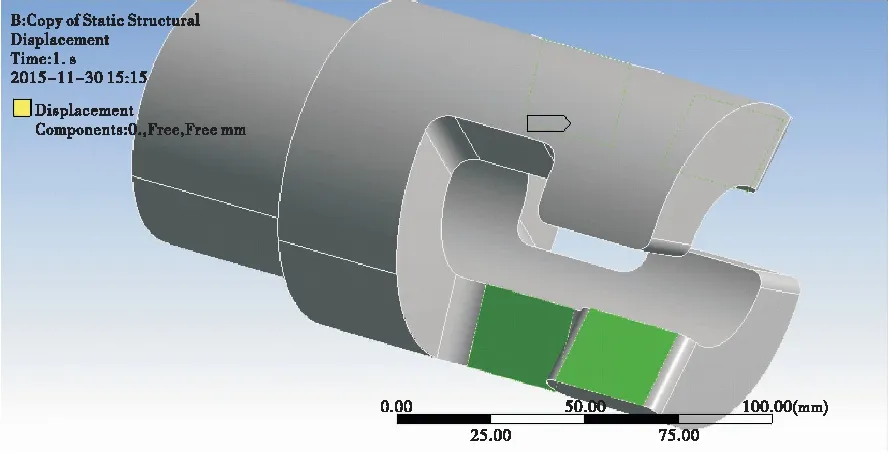
图7 受扭矩时的约束

经过计算，取 Von-Mises应力云图，最大应力σmax=104.2 MPa；小于材料的屈服极限，可以判断在800 N·m，挠性节并未屈服，满足设计要求，如图8所示。

图8 抗扭强度的Von-Mises应力云图

4 结 论

通过动力学仿真模型分析了内径和挠性节间隙对挠转角变化的影响，得出结论：在挠性节间隙相同的情况下，内径对挠转角的影响不大;随着挠性节间隙的增大，挠转角也在增大；挠性节间隙是影响挠转角度变化的主要因素。通过仿真计算完成了挠转角度的设计，采用有限元的方法校核了挠性节的拉伸强度和抗扭强度，保证了挠性短节满足设计指标要求。新研制的SDZ-8151挠性短节自2015年起在河南、新疆、陕北等多个油田的复杂水平井使用，用户反馈使用情况良好，解决了SDZ-8050挠性短节在复杂井况中被拉断的问题。