看！学生多聪明

蔡世阳

在九年级下册第27章第三节《用推理的方法研究四边形》中，例举了有关平行四边形判定的各类方法。在课后作业中，笔者布置了一道题目：“一组对边相等，一组对角相等的四边形是否为平行四边形，如果是，请加以证明，如果不是，请举反例说明。”布置这道作业题的背景是有关举反例的题目是近几年厦门市中考的热点。

本题可以用特殊的三角形进行举例说明：

①画△ABC，使∠C=90°，∠A=60°，∠B=30°；

②在BA上取BE=AC；

③以E为圆心，EB为半径，作弧，交AB于点D；

④连结DE。

在四边形AEDC中，易证∠A=∠EDC，DE=AC，但四边形AEDC并非平行四边形。

点评：本例用了特殊的三角形，具体的角度为学生所常见的，在具体操作中，以三角形为基础，所构建的四边形非平行四边形是易见的，操作过程并不困难。

引申与回味：本方法中限定的特殊角度，可以一般化，只需有∠A=2∠B，对∠C只需大于60°即可。

在2005～2006年市质检中，曾出过如下题目：

在△ABC的边AB和BC上，分别找点P和Q，使PQ=AC，∠PQC=∠A。

在当中的作答情况中，本题的得分率是全卷最低的一题，说明了学生在“举反例”这一类型的题目里思维容量是极大的，也是学生难以突破的一类题目。

以下将通过学生的几种解答方法，对本题“一组对边相等，一组对角相等的四边形是否为平行四边形，如果是，请加以证明，如果不是，请举反例说明。”做出解答：

方法一：

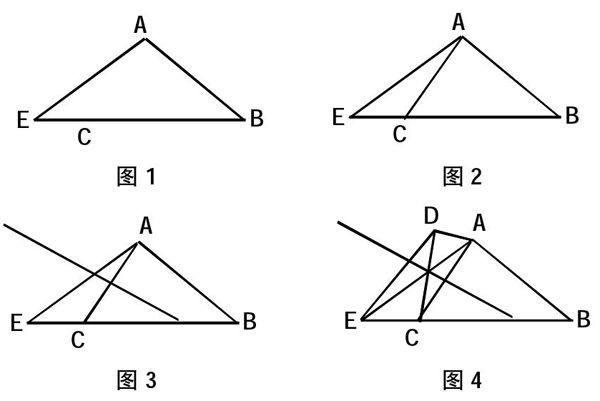
①画等腰三角形AEB，使AE=AB，如图1；

②在EB上取一点C（C不是EB中点），连结AC，如图2；

③以AC的垂直平分线为对称轴，作点E的对称点D，连结AD，如图3、4；

四边形ABCD即为所举反例。

由对称性可有：AE=CD，∠ADC=∠AEB，又∵AE=AB，∠AEB=∠B

∴CD=AB，∠ADC=∠B。

满足条件一组对边相等，一组对角相等，四边形ABCD并非平行四边形。

点评：本例中，利用等腰三角形固有的等边与等角，利用对称的形式确保边与角的不变性。顺利完成反例的列举，让人不由耳目一新。

引申与回味：①点C若为中点，则本解中四边形ABCD为平行四边形。

②对于对称边可表述为翻转△AEC，使点A、C位置互换，同样可以达到举例的效果。

③若等腰三角形的底角太小，则四边形ABCD可能作为凹四边形，只需改变等腰三角形的底角大小即可。

方法二：

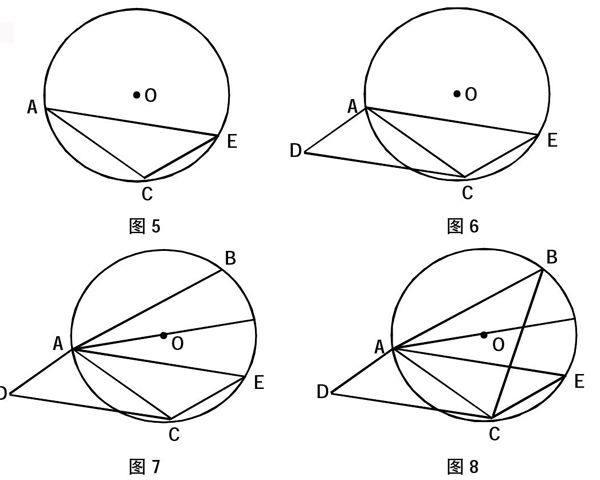
①作钝角△ACE和其外接圆O；如图5；

②作AD//CE，CD//AE，相交于点D；如图6；

③以直径AO为对称轴，作AE的对称弦AB；如图7；

④连结BC，四边形ABCD为所举反例；如图8。

四边形AECD为平行四边形。

故有AE=CD，则CD=AB，∠D=∠E=∠B，满足条件。

点评：本例在已建立的平行四边形的基础上，利用图保证边与角的不变，同时也运用了图的对称性，足以使人眼界大开。

以上的几种作答方法，是学生在考试中给出的，说明学生的思维形式并不仅仅局限于课堂所学、教师所教，教师应当在日常教学中，善于挖掘学生提供的优质素材，鼓励学生有自己独立的思考方式，千万不能低估了我们的学生，看，我们的学生多聪明！

（作者单位 福建省厦门市海沧区东孚学校）