一种基于相对钟差估计的星座自主时间同步方法*

卫星的自主导航主要包括卫星的位置计算和时钟误差(钟差)计算,即卫星自主定轨和自主时间同步.基于星间链路伪距测量的星座卫星自主导航系统实质上是一个测时—测距定位系统,星间距离测量精度与各卫星之间的时钟误差密切相关.因此,自主时间同步是基于星间链路伪距测量的星座自主导航的关键技术之一.

自主时间同步技术是随着GPS的自主导航技术的诞生而逐步发展的[1-3].目前国内外介绍自主时间同步的文献大多是针对导航星座开展研究的,并且以卫星的绝对钟差为估计参数[4-6].针对低轨区域星座自主导航的任务需求,本文提出一种基于相对钟差估计的星座自主时间同步方法.

1 自主时间同步方案

本文的研究对象是一个由3颗卫星组成的低轨区域星座,工作模式为组网工作,分为1颗主星和2颗副星.2颗副星在同一个轨道面上，分别和主星建立星间链路,可以提供伪距测量和星间通信.星座卫星示意图如图1所示.

由于缺少地面基准,用于自主时间同步计算的虚拟观测值仅包含2颗卫星的时钟相对钟差信息,不包含绝对钟差信息;而卫星之间的同步关系是由2颗卫星相对钟差估计的准确性决定的[7].因此,针对低轨区域星座本文提出选定主星0为基准星,假定其时间系统维持依靠地面进行,以副星和主星之间的相对钟差为状态变量,利用星载Kalman滤波进行实时估计,进而实现时间同步.其中,副星1与主星的相对钟差滤波过程在副星1的星载计算机上进行,副星2与主星的相对钟差滤波过程在副星2的星载计算机上进行;在时间同步过程中,主星通过星间链路将其钟差信息(由地面系统给出)传递给副星,副星利用滤波解算出的相对钟差估计值和接收到的主星钟差信息获得副星的钟差.

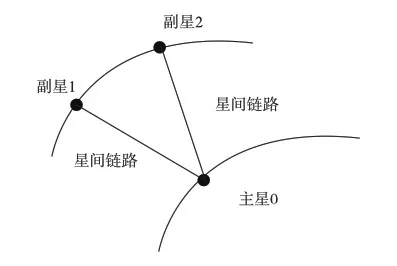
图1 星座卫星示意图

2 星座自主时间同步算法模型

2.1 时间系统状态模型

目前卫星上广泛采用的是铷钟.铷钟存在明显的频率漂移,采用钟差、频率偏差、频率漂移率描述其系统性变化.根据时钟微分方程[8],副星i(i=1,2)与主星之间的相对时钟微分方程可表示为

(1)

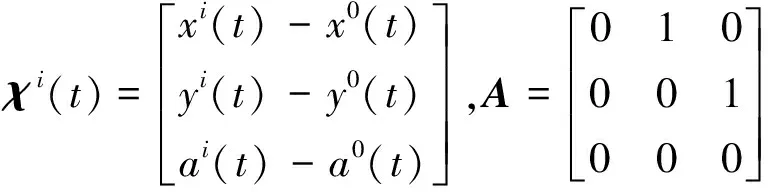
Ewi(t)(wi(t+τ))T

=qδ(τ)

(2)

式中,q=2×diag{q1,q2,q3}为系统噪声过程向量wi(t)的方差强度阵,分量q1、q2、q3具体可以通过Hadamard方差得到.

离散化的状态方程写为

(3)

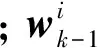
(4)

(5)

2.2 测量方程

设星座中有2颗相互可见的卫星i和卫星j,对于某一参考历元tk可以写出星间双向伪距测量方程为

(6)

(7)

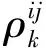
从而得到用于时间同步计算的虚拟观测值为

(8)

从式(8)可以看出时间同步虚拟观测值的特性如下：1)与卫星星历无关;2)包含2个卫星时钟相对钟差信息;3)不包含绝对钟差信息.

于是,以副星i(i=1,2)与主星的相对钟差为状态变量,相应的测量方程写为

(9)

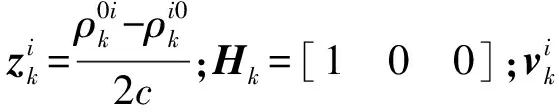
2.3 Kalman滤波基本方程

基于式(3)的时钟系统状态方程和式(9)的测量方程,问题转化为随机线性定常系统的估计问题.由于对每个星载滤波器等价,下面的公式省略上标i，可以写出下列适用于星座卫星铷原子钟时间同步的标准Kalman滤波基本方程[9]：

时间更新

(10)

(11)

测量更新

(12)

(13)

(14)

3 仿真研究

对本文所提出的基于相对钟差估计的星座自主时间同步方法进行仿真验证.在此定义副星i的时间同步误差为

(15)

(16)

仿真条件如下：

1)真实时钟由时钟微分方程积分得到.每颗卫星搭载的原子钟的初始钟差、初始频率偏差及初始频率漂移率分别为20ns、0、0,时钟噪声系数分别取q1=1.11×10-22,q2=2.22×10-32,q3=6.66×10-45;

2)状态先验初值为χ0=[5ns,2×10-12Hz,3×10-18s/s2]T,先验初始方差为P0=2×diag{(5)2,(2×10-12)2,(3×10-18)2};

3)星间等效伪距测量误差为1m；

4)仿真时间为30d,滤波周期为60s.

若30d内无任何观测对时钟钟差进行修正,则可以计算得到星座中2颗副星的时钟误差曲线,如图2所示.由于随机数的产生,每次仿真的钟差数值会有所不同,但总体趋势相同,量级基本相同.

图2 卫星钟差

由此可见,若不对钟差进行修正,则30d后其时钟误差将达到3000ns,由此产生的等效测距误差约为0.9km,这一数值对基于星间链路的星座自主导航系统的影响非常大.

根据本文所介绍的基于相对钟差估计的星座自主时间同步方法,如果利用星间双向伪距测量数据,经过星载Kalman滤波可得到副星与主星之间的相对钟差估计值.假定主星的钟差信息已知,则可计算出副星的钟差信息.通过数学仿真得到的时钟同步误差曲线见图3～5.由曲线可看出,利用本文介绍的基于相对钟差估计的时间同步方法是完全可行的,经统计其时间同步精度达2.4557ns,且同步误差不随时间积累.

4 结 论

本文针对低轨区域星座,提出了一种基于相对钟差估计的星座时间同步方法.该方法以星座成员卫星与基准星之间的相对钟差为状态变量,利用星间双向伪距测量数据,经过星载滤波器直接估计出卫星与基准星的相对钟差,因此不需要估计出各卫星的绝对钟差.仿真结果表明,基于相对钟差估计的星座时间同步方法是完全可行的,且同步误差稳定不随时间积累.

针对其他构型的区域星座,可根据实际情况选择基准星，如可将与星座中其他成员卫星都存在星间链路的卫星作为基准星；若不存在满足该条件的卫星，则选可见卫星最多的卫星作为基准星，此时，对于与基准星直接可见卫星，其相对钟差可利用本文提出的方法直接求出，对于与基准星不可见卫星，可先计算出与其他可见卫星的相对钟差，然后换算成与基准星的相对钟差.该方法的唯一缺点是：基准星的钟差信息需要地面系统给出,所以该方法不是完全自主的.

参 考 文 献

[1]Kiser K, Vaughan S H. GPS ⅡR joins the GPS constellation[C] . The 11thInternational Technology Meeting of the Satellite Division of the Institute of Navigation, Nashville, USA, September 15-18， 1998

[2]Fontana R D, Cheung W, Stansell T. The modernized L2 civil signal: leaping forward in the 21st century[J]．GPS World,2001,11(9): 28-34

[3]李孝强,杨文强.导航卫星系统自主导航技术及其发展趋势[J].中国航天, 2005(3): 33-36

[4]Ananda M P, Bernstein H. Global positioning system(GPS) autonomous navigation[C]．IEEE Position, Location and Navigation Symposium, Las Vegas, USA, March 20-23,1990

[5]帅平.导航星座的自主导航技术——卫星自主时间同步[J].飞行器测控学报, 2004, 23(4): 11-15

Shuai P. Autonomous navigation technology for navigation constellation: autonomous synchronization among satellites [J]. Journal of Spacecraft TT & C Technology, 2004, 23(4): 11-15

[6]顾亚楠,陈忠贵,帅平.基于Hadamard方差的导航星座自主时间同步算法研究[J].中国空间科学技术, 2010, 30(1): 1-9

Gu Y N, Chen Z G,Shuai P. Autonomous time synchronization algorithm on Hadamard variance among navigation satellites [J]. Chinese Space Science and Technology, 2010,30(1): 1-9

[7]徐冬梅,杨龙.利用条件平差实现导航星座自主守时方法[J].中国空间科学技术, 2006, 26(6): 18-23

Xu D M, Yang L. Auto-timing of satellite navigation system using conditional estimate [J]. Chinese Space Science and Technology, 2006,26(6): 18-23

[8]郭海荣.导航卫星原子钟时频特性分析理论与方法研究[D].郑州：解放军信息工程大学,2006

[9]秦永元,张洪钺,汪淑华.卡尔曼滤波与组合导航原理[M].西安: 西北工业大学出版社,1998,182-187