基于参数自整定速度控制器SGCMG框架伺服控制系统*

单框架控制力矩陀螺(SGCMG)框架转速的控制性能直接影响着控制力矩陀螺整机的输出力矩，是控制力矩陀螺产品最关键的特性之一.影响控制力矩陀螺控制性能的因素包括：力学或温度条件的变化，结构参数及负载特性的变化，各种扰动力矩的干扰等，这些扰动力矩包括：星体转动时产生的低频的扰动力矩，高速转子扰动力矩[1]，地面实验过程中，还会有框架角位置改变引起摩擦力矩的变化[2]，电机力矩波动[3]及轴承摩擦力矩.

在框架伺服系统控制方法方面，PID控制是较早发展起来的一种基于经典控制理论的控制策略，但传统PID控制策略难以兼顾大转速范围内的高性能动静态控制要求.文献[4]分析了PID控制性能的不足，提出了基于DSP改进的控制方法，这种方法是在系统稳定性和控制精度之间进行折中，牺牲了一定的系统稳定性来保证控制精度.文献[5]给出了抑制低速爬行的方法，阐明了低速爬行和PID控制参数的关系，但单一的参数不能满足不同负载的控制要求.文献[6-8]给出了不同的转速计算方法、扰动力矩和摩擦力矩的补偿算法，这些都是基于传统PID的改进算法，实现了对影响框架伺服系统转速控制的非线性扰动力矩的有效抑制，但仍无法彻底解决单一系统参数不能满足系统的控制要求的矛盾.

模糊控制技术是建立在模糊数学的基础上的，它是针对被控对象的数学模型不明确，或非线性模型的一种工程实用、实现简单的控制方法.在控制力矩陀螺的应用场合，需要电机在全工况下具备良好的速度控制特性.在在线计算能力有限的条件下，基于模糊逻辑的非线性控制方法是电机控制的理想选择之一[9-11].

本文针对使用无刷直流电机的单框架控制力矩陀螺框架伺服系统，设计了基于模糊控制策略及参数自整定控制器的PI控制方法.该方法使控制力矩陀螺框架伺服系统有良好的动、静态性能，且获得了更好的跟踪能力.

1 框架伺服系统及控制策略

1.1 无刷直流电机全桥功率驱动模型

低速框架电机采用无刷直流电机(BLDC, brushless DC motor)，驱动采用全桥驱动，采用任一时刻两相导通一相截止，三相六状态的120°导通方式.驱动电路等效模型如图1所示.

图1 无刷直流电机驱动系统等效模型

假定：三相绕组完全对称，气隙磁场为方波，定子电流、转子磁场分布对称；忽略齿槽、换相过程和电枢反应等的影响；电枢绕组在定子内表面均匀连续分布；忽略磁路饱和因素，不计涡流和磁滞损耗.由上述假设，可得电机状态方程

(1)

式中，eA，eB，eC为定子相绕组反电势(V)；定子各相绕组电阻相等为R(Ω)；定子各相绕组自感相等为L(H)；定子相绕组间互感LAB，LAC，LBA，LBC，LCA，LCB为常数M(H)，与转子位置无关.

电磁转矩方程

Te=(eAiA+eBiB+eCiC)/ω

(2)

框架伺服系统动力学方程为

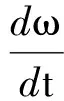
(3)

式中，J为框架轴向转动惯量；ω为电机机械角速度；Te为电磁力矩；Tf为扰动力矩；ke为电机力矩系数；i为电机电流.

1.2 框架伺服系统结构

框架伺服系统采用无刷直流电机，并通过谐波减速器来实现间接驱动，如图2所示.

图2 采用转速-电流闭环PI控制的系统结构

系统采用双闭环(速度环、电流环)控制.BLDCM及其驱动系统主要由电机本体、旋转变压器及驱动电路等组成.采用旋转变压器对框架电机转子位置进行采集，进而得到需要的电机转速.利用霍尔信号为逆变器提供相应的换相信号.

PI控制器的本质是一种线性调节器，而对于具有强非线性特性的被控对象,或对于大范围内有高性能的动静态控制要求的被控对象,传统的PI控制难以保证设计性能指标.

2 基于参数自整定速度控制器设计

针对上述分析，本文对转速、电流双闭环系统的传统PI控制进行改进，采用参数自整定模糊控制器来实现速度控制器，通过在线实时修正控制器参数，达到提高控制性能的目的.

2.1 无刷直流电机参数自整定控制器模型

无刷直流电机模糊控制的方法主要可分为标准模糊控制器、模糊PID切换控制器、优化模糊控制器和模糊预补偿控制器几大类[12]. 目前广泛采用二维模糊控制器，它以反馈误差和误差的变化作为输入量，以控制量的变化为输出变量.

本文设计了一种基于模糊推理的参数自整定控制器：利用模糊前馈补偿控制器，根据系统的实际参考输入，对PI控制器的参数进行在线自整定，得到了理想控制器参数，然后通过双闭环控制器对框架伺服系统进行控制.参数自整定控制器原理图如图3所示.

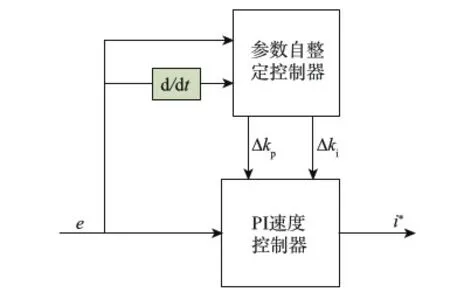
图3 参数自整定控制器原理

ki=ki0+kui×Δki

(4)

kp=kp0+kup×Δkp

(5)

其中kp0，ki0为PI参数初值，kui、kup是比例因子,实现PI参数的自整定功能.

2.2 基于模糊推理的参数自整定控制器设计

输入、输出变量的隶属度函数关系相同，均选用三角隶属函数关系，如图4所示.

图4 隶属度函数关系图

2.3 模糊控制规则与控制机理

基于上述模糊控制规则，采用如下控制机理：

1)参数自整定模糊Pl控制的速度环在外，传统PI控制的电流环在内；

3)电流调节采用传统PI控制方法进行调节.响应速度快，对电压波动起及时抗扰作用；在转速调节过程中(当负载变化时)，使电流跟随给定电压变化.

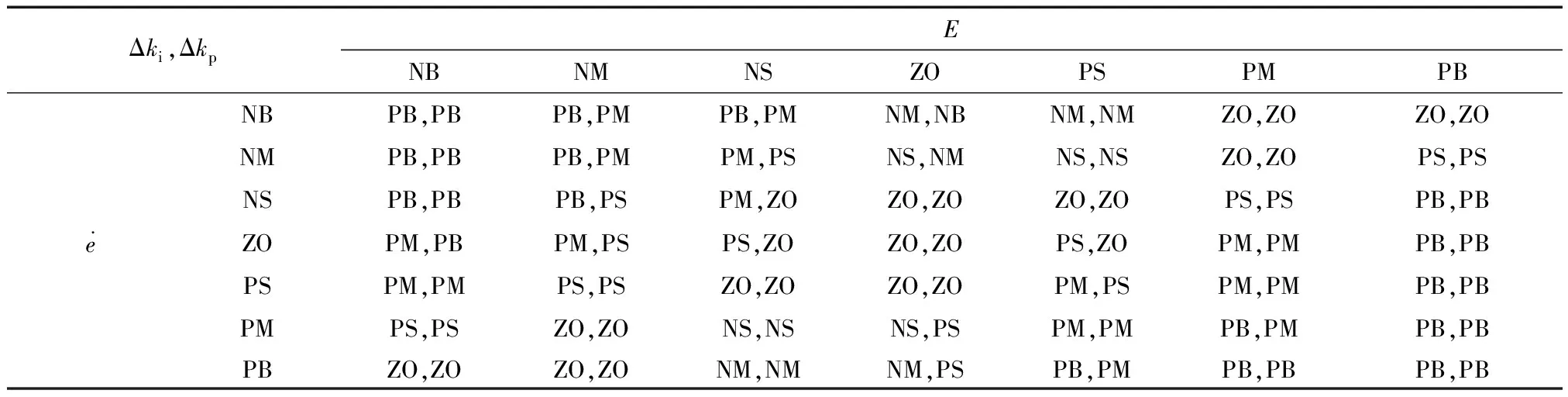
表1 模糊PI规则控制集

图5 模糊PI控制器Δkp、Δki输入输出关系曲面图

3 仿 真

在Matlab/Simulink平台上搭建框架无刷直流电机控制系统，分别对传统PI控制器和本文设计的参数自整定模糊控制行仿真研究.

仿真验证设计原则如下：

1)传统PI控制器的kp,ki与基于模糊规则的参数自整定速度控制器的kp0,ki0选择同一组参数；

2)给定转速验证两种控制器的动态性能，稳态后，改变转速，看两种控制器的跟踪性能；

3)在稳态下突加扰动，比较两种控制器的抗干扰能力及控制的鲁棒性.

仿真参数如表2所示.

仿真试验如下：1)首先给定2(°)/s的转速，在0.2s处改变框架转速，比较两种控制方法的控制效果如图6(a)所示；2)给定2(°)/s的转速，在0.2s处突加0.01N·m的负载扰动比较两种控制方法，结果如图6(b)所示.

表2 仿真实例参数说明

图6 PI控制与模糊控制转速曲线

从图6中可以看到,基于模糊逻辑的参数自整定速度控制器的控制性能相对于传统PI方法,有一定优势：转速响应速度快，上升时间较短，缩短了约60%，超调减小约20%.转速变化时，跟踪性能好；突加负载扰动时，转速脉动得到了较好抑制.基于模糊逻辑的参数自整定速度控制系统动态性能更好，跟踪性能高,稳定性好,鲁棒性强.

4 结 论

参数自整定速度控制器充分利用了模糊规则少、应用简单灵活、具有自适应能力的优势，用于在线确定控制作用的时间很短，实时性强.针对控制力矩陀螺框架伺服系统PI控制的能力不足的问题，基于模糊PI控制策略的参数自整定速度控制器与传统PI控制相比，有很好的动态性能和稳态性能，跟踪性能高，同时该控制器对框架伺服系统所受扰动有很好的鲁棒性.

参 考 文 献

[1]金磊，徐世杰. SGCMG框架伺服系统动力学建模与低速控制[J]. 中国空间科学技术，2010，30(6)：1-10

Jin L, Xu S J. Dynamics modeling and low rate control of gimbal servo system for single gimbal control moment gyro [J]. Chinese Space Science and Technology, 2010，30(6)：1-10

[2]王鹏,房建成. MSCMG框架伺服系统非线性摩擦力矩建模与实验研究[J]. 宇航学报，2007，28(3)：613-618

Wang P, Fang J C. Nonlinear dynamic modeling and experimental study of friction moment for gimbal servo system used in magnetically suspended control moment gyroscope [J]. Journal of Astronautics, 2007，28(3)：613-618

[3]吴忠, 吴宏鑫. SGCMG 框架伺服系统扰动力矩的分析与抑制[J]. 航天控制, 1998,16(4): 9-17

Wu Z, Wu H X. Analysis and attenuation of disturbance torque in SGCMG gimbal servo systems[J] . Aerospace Control, 1998, 16(4): 9-17

[4]黄体笋，魏新生，刘付成，等. 基于DSP的控制力矩陀螺框架数字伺服系统[J].计算机测量与控制，2009，17(2)：349-359

Huang T S,Wei X S，Liu F C，et al. Digital servo system for gimbal of control moment gyro based on DSP[J]. Computer Measurement & Control， 2009，17(2)：349-359

[5]张锦江，吴宏鑫，李季苏，等. 高精度伺服系统低速问题研究[J].自动化学报，2002，28(3)：431-434

Zhang J J, Wu H X, Li J S, et al. On low speed problem of high precision servo system[J]. Acta Automatica Sinica, 2002，28(3)：431-434

[6]鲁明，李耀华，张激扬，等. 控制力矩陀螺框架伺服系统的超低速测速方法[J]. 中国惯性技术学报, 2012, 20(2):234-238

Lu M, Li Y H, Zhang J Y, et al. Ultra-low speed detection method for CMG gimbal servo systems[J]. Journal of Chinese Inertial Technology, 2012, 20(2):234-238

[7]张激扬，周大宁，高亚楠. 控制力矩陀螺框架控制方法及框架转速测量方法[J]. 空间控制技术与应用，2008，34(2)：23-28

Zhang J Y, Zhou D N, Gao Y N. Gimbal control technique and gimbal rate measurement method for the control moment gyro[J]. Aerospace Control and Application, 2008, 34(2): 23-28

[8]Ming C C, Cang M L. Dynamic control and diagnostic friction estimation for an SPMSM driven satellite reaction wheel[J]. IEEE Transactions on Industrial Electronics, 2011, 58(10): 4693-4707

[9]Chen W, Xia C L. Sensorless control of brushless DC motor based on fuzzy logic[C]. IEEE Proceedings of the World Congress on Intelligent Control and Automation,DaLian, 2006

[10]Xia C L, Xiu J. Sensorless control of switched reluctance motor based on ANFIS[C]. International Conference on Neural Information Processing,HongKong, 2006

[11]Rubaai A, Ricketts D, Kankam M D. Experimental verification of a hybrid fuzzy control strategy for a high-performance brushless DC drive system[J]. IEEE Transactions on Industry Applications, 2001,37(2):503-512

[12]夏长亮.无刷直流电机控制系统[M].北京：科学出版社.