拍合式电磁阀动态响应仿真分析与试验验证*

电磁阀是航天推进系统中重要的部件之一，由阀体组件、电磁线圈、阀座、阀芯组件(包括弹簧)等组成，是航天推力器的推进剂通断控制阀门.电磁阀的开启与关闭时间会影响到航天器的控制精度，是发动机或推力器的重要指标之一.

利用计算机仿真可以得到电磁阀的响应时间等结果，在设计工作中有重要地位.文献[1-2]利用有限元方法分析了线圈匝数与非工作气隙对响应时间的影响；文献[3-4]利用AMESim中的电磁铁集成模块建模，未对磁路进行分解；文献[5]研究了负载时影响螺旋弹簧结构电磁阀响应时间的部分因素.

本文分别利用有限元方法和磁路分析法建立了拍合式电磁阀的仿真模型，对两种仿真方法进行对比.定量分析了影响电磁阀电性能的因素，包括：弹簧刚度、弹簧预变形、非工作气隙、衔铁质量及放电回路电阻，且仿真模型得到了试验验证.图1为仿真对象的结构简图.

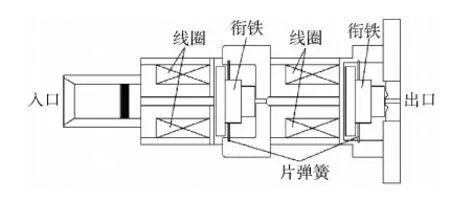
图1 电磁阀结构示意图

1 数学模型

1.1 有限元模型

已知描述空间电磁场的数学描述为：

(1)电磁感应定律

(1)

式中，e为感应电动势，Ψ为磁链，N线圈匝数，Φ为磁通量.

(2)电压平衡定律

(2)

式中，u为电压，i为线圈电流，R为线圈电阻.

(3)全电流定律

∮lH·dl=∑iN

(3)

式中，H为磁场强度向量，l为积分路径，视磁路计算的需要和方便来选取[4].

1.2 磁路模型

根据基尔霍夫磁压定律，可得磁路方程

iN=Φδ(2Rδ+Rf+ΣRm)

(4)

(5)

(6)

式中，i为线圈中的激励电流，N为线圈匝数，Φδ为工作气隙磁通量，Rδ为工作气隙磁阻，Rf为非工作气隙磁阻，Rm为磁路磁阻，δ为工作气隙，μ0为空气中磁导率，Sδ为气隙截面积，lm为导磁材料长度，μm为导磁材料磁导率，Sm为导磁材料截面积.

1.3 动力学模型

(7)

式中，FM为电磁吸力，m为衔铁质量，c为弹簧刚度，F0为初始负载力，A为受力面面积，

可见，影响电磁阀时间性能的参数主要有：线圈匝数、线圈电阻、衔铁质量、气隙、弹簧刚度和弹簧初始变形[5].

2 仿真模型的建立

2.1 有限元模型

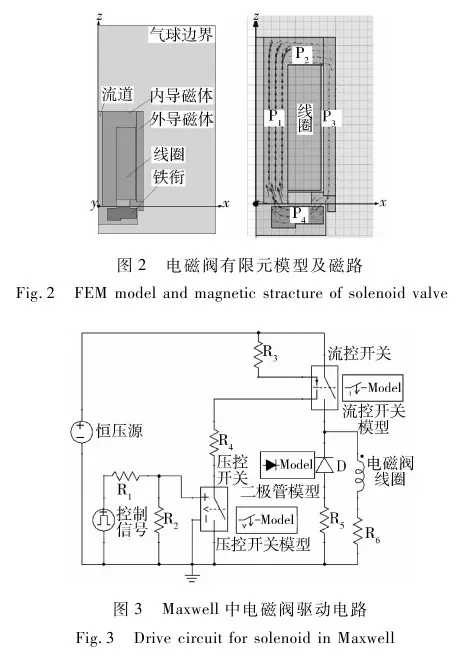
有限元仿真利用Ansoft公司的Maxwell 2D软件进行计算，计算模型及磁路分布如图2所示.根据电磁阀实际驱动电路设置外部驱动，图3所示为利用Maxwell Circuit Editor编辑的可嵌入有限元模型中的驱动电路.按照产品的初步设计参数，设置驱动电压为27V，线圈匝数2000匝，线圈电阻50Ω，非工作气隙为0.04mm，衔铁位移0.4mm，衔铁质量6g，弹簧初始变形0.3mm，弹簧刚度15N/mm，设置磁材料B-H曲线.

2.2 磁路模型

图2右栏为电磁阀磁路示意图.根据电磁阀的结构特点，将其分为P1、P2、P3、P4及线圈共5个部分.根据电磁铁的实际结构尺寸及材料建立磁路模型如图4所示.参数设置与有限元模型一致.

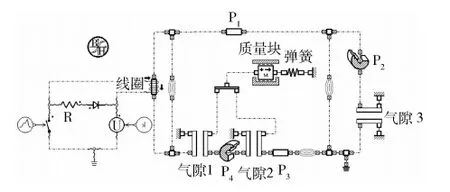
图4 AMESim电磁阀仿真模型

3 影响参数分析

3.1 弹簧刚度及初始变形

从电磁阀的电性能考虑，弹簧的刚度与预紧力越小，开启时间就越短，但关闭时间则越长；从阀门的密封性能(在密封比压范围内)来考虑，弹簧的刚度与预紧力越大，密封性就会越好.所以，为了保持电磁阀的整体性能，需选择一个合适的刚度和预紧力.改变弹簧刚度及预变形，可得到对应的响应时间，如表1所示.

表1 不同弹簧刚度下的弹簧预变形与时间的关系

可以看出弹簧刚度越大，则开启时间越长、关闭时间越短；预变形量越大，则开启时间越长、关闭时间越短.

3.2 衔铁质量

衔铁组件是电磁阀中的运动部件.当衔铁截面积不变，即电磁力一定时，衔铁质量的大小影响阀门开关响应时间，如图5所示.可见，衔铁质量越小，开启与关闭时间均会缩短，而且会减小电磁阀整体质量.

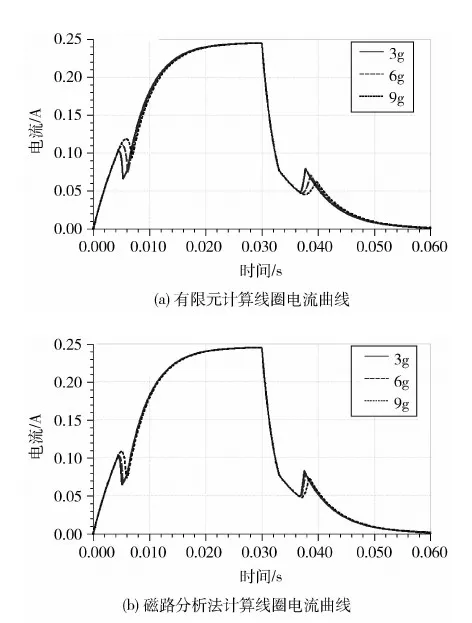
图5 衔铁质量与响应特性的关系

3.3 放电回路电阻

驱动电路为电磁阀提供电源.打开时，提供恒定电压；断电时，为了达到迅速关闭的目的，需有一个合适的放电回路，使线圈中的电能得到释放.放电回路中电阻的大小对电磁阀关闭时间有一定影响，如图6所示.放电回路电阻只影响关闭时间.当需单独调节关闭时间时，可以调节电阻R的大小.

3.4 非工作气隙

为了有效消除导磁材料剩磁对释放时间的影响，一般都有意识的增加一个固定的非工作气隙.仿真时通过增加外导磁体与线圈骨架的间隙，发现随着间隙的增大，开启时间会增加，关闭时间会显著缩短，这是由于电磁力减小造成的.电磁阀设计允许的非工作气隙范围为0.032mm～0.105mm之间.保持其他参数不变，设置不同的非工作气隙，可得出它对电磁阀时间特性的影响.

从图7可以看出，非工作气隙越大，开启时间越长，关闭时间越短.通过控制零件尺寸公差，可以选择合适的开启与关闭时间.

3.5 线圈匝数

线圈匝数决定了线圈的电感、电阻与磁路中磁势的大小.改变线圈匝数，电阻不变，进行仿真，结果如图8所示.可以看出，线圈匝数越多，开启/关闭电流越小，开启/关闭时间越长.

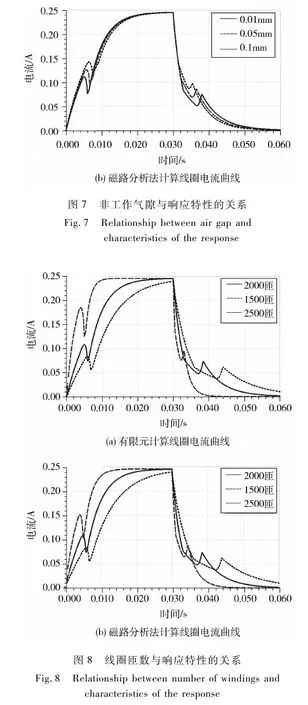
线圈匝数的改变会影响磁路磁势，从而影响衔铁受到的电磁力，如图9所示.线圈匝数越多，电磁力越大.可见，线圈匝数增多后，电磁力的增加不足以克服电感增加引起的电流上升速度的减小对响应时间的影响.所以，在保证电磁吸力满足设计指标的情况下，可选取较少的匝数以缩短开启/关闭时间.

图9 线圈匝数与电磁吸力的关系

3.6 结果分析

综合以上计算结果发现，各参数与响应时间之间均近似为线性关系.以电磁阀的设计参数，即仿真计算的初始设定值为基础，当开启/关闭时间每增加0.1ms时，各参数的变化率如表2所示.

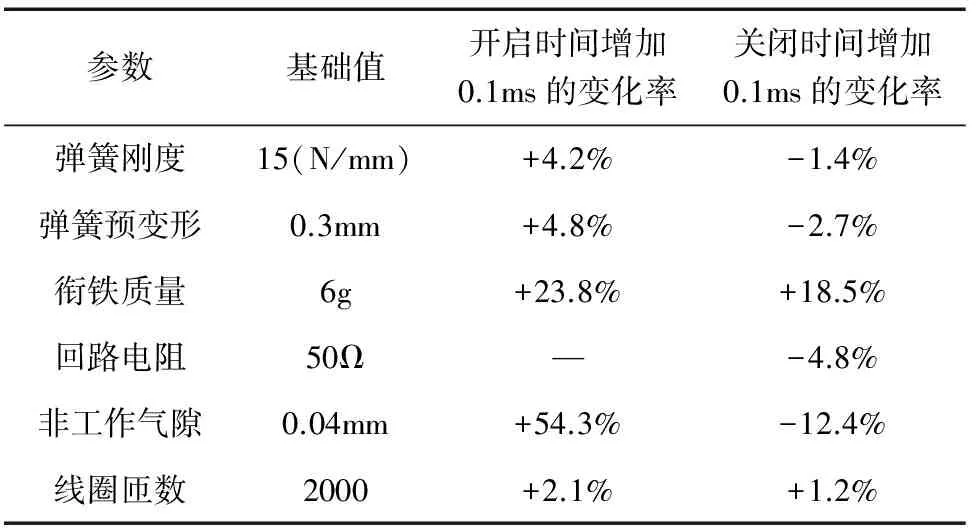
表2 各参数对时间性能的影响程度

产品研制时，衔铁质量、线圈匝数控制相对容易；片弹簧刚度、弹簧预变形量、非工作气隙等量不易控制.因此，电磁阀在设计时应综合考虑加工与装配条件，合理选择关键零件的上下公差，使响应时间满足设计指标.

4 两种仿真计算及试验结果对比

共对6台电磁阀做了电性能测试，开启时间5.98ms～6.84ms，平均为6.41ms，有限元仿真结果为6.4ms；磁路仿真计算结果为6.2ms；关闭时间7.42ms～9.28ms，平均为8.41ms，有限元仿真结果为8.4ms；磁路仿真计算结果为8.6ms.两种仿真计算结果与试验结果一致性均较好.图10为试验结果的平均值与设计参数下的仿真计算结果.

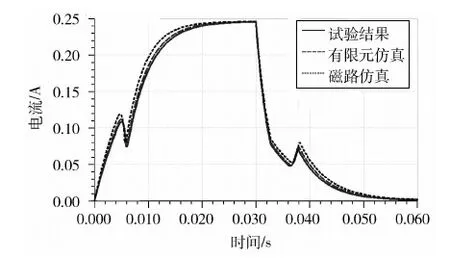
图10 电磁阀电流曲线

为研究各参数的影响程度，将进行完电性能测试后响应时间有较大差异的2台电磁阀进行了解剖，测量出产品的可测参数值如表3所示，可见，弹簧的实际刚度值会在设计值附近上下波动.将测得参数值输入仿真模型，结果如表4所示.可以看出，仿真结果与试验结果的变化趋势保持一致，验证了仿真模型的准确性.

表3 阀门各参数测量值

表4 试验结果与仿真结果对比

虽然有限元法计算速度慢，但从整体上看，计算结果更接近试验结果.因此，磁路模型可用在电磁阀设计工作的前期，进行快速的方案论证；有限元模型则可在对设计参数的微调时使用.

5 结 论

(1)本文为一种拍合式电磁阀建立了带有外部驱动电路的有限元模型与磁路模型，仿真计算结果与试验结果有较好的一致性.

(2)定量分析了影响电磁阀响应时间的因素：弹簧刚度、弹簧预变形、非工作气隙、衔铁质量、放电回路电阻及线圈匝数，可以为以后的设计工作提供借鉴.

(3)为了加快设计速度，前期可用磁路分析模型进行方案论证，后期可用有限元法微调设计参数.

(4)综合考虑到生产加工时的可控性及表2所示结果，弹簧刚度在影响电磁阀电性能的因素中占有重要地位，在设计、生产工作中应予以重视.

参 考 文 献

[1]张榛.电磁阀动态响应特性的有限元仿真与优化设计[J]. 空间控制技术与应用，2006，34(5)：53-56

Zhang Z. FEA simulation of dynamic response of solenoid valve and it’s optimal design [J]. Aerospace Control and Application，2006，34(5)：53-56

[2]张功晖，黎志航，周志鸿.基于Maxwell方程的电磁阀开启过程动态特性仿真研究[J].液压气动与密封，2010,30(11):22-25

Zhang G H, Li Z H, Zhou Z H. Simulation research of dynamic character of solenoid valve’s opening process based on Maxwell equation[J]. Hydraulics Pneumatics & Seals,2010,30(11):22-25

[3]袁洪滨，张民庆，孙彦堂.基于AMESim的直动式电磁阀动态仿真研究[J].火箭推进，2011，37(5)：30-35

Yuan H B，Zhang M Q，Sun Y T. AMESim-based simulation analysis of dynamic characteristics of direct-acting solenoid valve [J].Journal of Roket Propulsion，2011，37(5)：30-35

[4]王扬彬，徐兵，刘英杰.基于Ansoft及AMESim的电磁铁动态特性仿真分析[J].机床与液压，2008，36(9):104-108

Wang Y B, Xu B, Liu Y J. Simulation analysis of the dynamic characteristics of the solenoid based on Ansoft and AMESim[J]. Machine Tool & Hydraulics,2008,36(9):104-108

[5]Viktor S，Janos V. Computational and experimental investigation on solenoid valve dynamics[C]. International Conference on Advanced Intelligent Mechatronics Proceedings，Como，Italy,July 8-12，2001

[6]李泉凤. 电磁场数值计算与电磁铁设计[M]．北京：清华大学出版社，2002

[7]朱宁昌. 液体火箭发动机设计[M]．北京：中国宇航出版社，1994