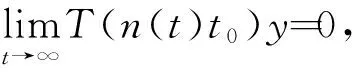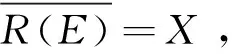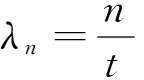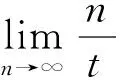广义算子半群渐近行为及其强弱稳定性

仓定帮，陈 藏，葛世刚

(华北科技学院,北京 101601)

自1942年，为了解决偏微分方程的初值问题，以Hille与Yosida为代表的一些数学家提出了Banach空间上强连续C0半群理论。此后，算子半群理论得到了不断的充实与发展。根据不同应用背景，C半群、积分半群等理论不断被提出[1-5]，在解决偏微分方程领域起着非常重要的作用。分布参数控制系统，现代航天技术等工程领域中引人注目的问题的数学模型均为其有力的背景。

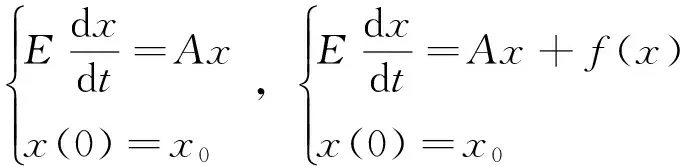
1 定义与引理

定义1[6]设E是Banach空间上的有界线性算子，A是闭线性算子，称ρ(E,A)={λ:λ∈C,(λE-A)-1是Banach空间上的线性算子}为算子A的广义预解集，ρ(E,A)的余集称为A的E广义谱集，记为σ(E,A)。对λ∈ρ(E,A)，称R(λE,A)=(λE-A)-1为A的E广义预解式。

定义2[6]设X是Banach空间，B(X)是X上的有界线性算子全体，设单参数算子{T(t)}t≥0∈B(X)，E是一个有界线性算子，若T(t+s)=T(t)ET(s),∀t,s≥0，则称{T(t)}t≥0是由E引导的广义算子半群，简称广义算子半群。

定义3[6]设A是X中的闭稠定线性算子，{T(t)}t≥0是强连续有界线性算子，且存在M>0，ω0∈R，使得‖T(t)‖≤Meω0t成立，E是一个有界线性算子，若下面的式子成立

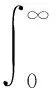
此时{T(t)}t≥0称为由E引导的以A为生成元的指数有界的广义算子半群。

引理1 若{T(t)}t≥0称为由E引导的以A为生成元的指数有界的广义算子半群，则下面的结论成立：

(i)T(t)T(s)=T(s)T(t)，∀s,t≥0;

下面证明(ii)，∀x∈D(A),Reλ>ω0有

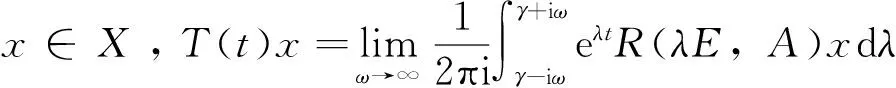
引理3[6]设{T(t)}t≥0称为由E引导的以A为生成元的强连续广义算子半群，则∀x∈X有

并且上述的极限在t的任何有界区间上是一致的。

2 广义算子半群的渐近行为

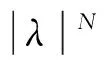
定理1 设{T(t)}t≥0为由E引导的以A为生成元的指数有界的广义算子半群，Reσ(E,A)≤-σ<0。若预解式增长阶假设对N≥2成立，则存在μ>0，0<μ<σ，K(μ)>0，使得‖A-(N+2)T(t)E(N+2)x‖≤K(μ)e-μt‖x‖成立。

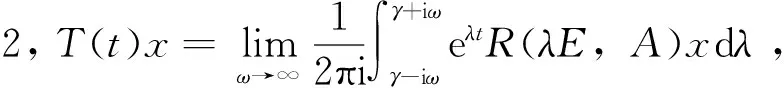
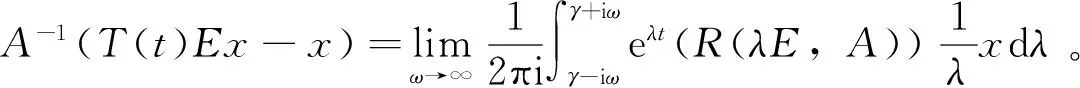
因为{T(t)}t≥0是指数有界的，经过简单的计算有

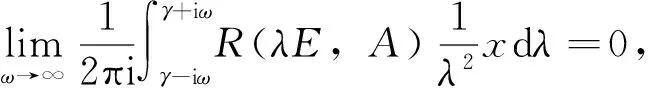
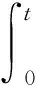
A-2T(t)E2x-A-2Ex-A-1tx=

继续积分可得

(2)

令-σ<-μ<0，使得当-μ≤Reλ≤γ时预解式增长阶假设成立。定义曲线C=Γ1+Γ2+Γ3+Γ4，其中Γ1={γ+iy;-ω≤y≤ω}，Γ2={x+iy;-μ≤x≤γ}，Γ3={-μ+iy;-ω≤y≤ω}，Γ4={x-iω;-μ≤x≤γ}。因为

也即

3 广义算子半群的强弱等价性

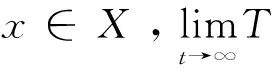
一般来说，指数稳定，强稳定与弱稳定不等价，指数稳定可推出强稳定，强稳定可推出弱稳定。下文主要研究了广义算子半群的强弱稳定性等价的条件。

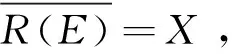
证明假设{T(t)}t≥0是弱稳定的，则根据题设条件和一致有界定理可知‖T(t)‖≤M，t0>0。

且T(nt0)E=T(t0)ET(t0)E…T(t0)E=ET(nt0)。∀t>t0，令t=n(t)t0+α(t)，n(t)∈N，0≤α(t)

则n(t)t0=t-α(t)>t-t0→∞，t→∞。

‖T(t)Ey‖=‖T(α(t))ET(n(t)t0)Ey‖

≤M‖E2T(nt0)y‖=M‖E2T(nt0)y‖，∀y∈X

(i) 存在λ0∈ρ(E,A)使得ER(λ0E,A)=R(λ0E,A)E；

(ii)EA⊂AE；

(iii) ∀λ∈ρ(E,A)，ERn(λE,A)=Rn(λE,A)E，n∈N；

(iv)ET(t)=T(t)E。

有(i) ⟹ (ii) ⟹ (iii) ⟹ (iv)。

证明 (i) ⟹ (ii) ∀x∈D(A)，令(λ0E-A)x=y，则x=R(λ0E,A)y，从而有

Ex=ER(λ0E,A)y=R(λ0E,A)Ey∈D(A)

进一步计算可得

EAx=λ0E2x-E(λ0E-A)x=

λ0R(λ0E,A)E2y-Ey=

[λ0E-(λ0E-A)]R(λ0E,A)Ey=AEx

即可证得：EA⊂AE。

(ii) ⟹ (iii) ∀λ∈ρ(E,A)，∀x∈X，令R(λE,A)x=z，则z∈D(A)，并且

E(λE-A)z=λE2z-EAz=

λE2z-AEz=(λE-A)Ez

即得R(λE,A)E=ER(λE,A)，进而可知Rn(λE,A)E=ERn(λE,A)。

(i)存在λ0∈ρ(E,A)，使得R(λ0E,A)Ex=ER(λ0E,A)x；

(ii)EA⊂AE。

则{T(t)}t≥0的强弱稳定性等价。

证明由定理3可知，上述条件之一成立时定理2的条件成立，从而根据定理2可知{T(t)}t≥0的强弱稳定性等价。

参考文献：

[1] TANAKA N, MIYADERA I. Exponentially boundedC-semigroups and integrated semigroups [J]. Tokyo J Math, 1989, 1: 99-115.

[2] NEUBRANDER F. Integrated semigroups and application to the abstract Cauchy problem [J]. Pacific J of Math, 1988, 135(1): 111-155.

[3] ZHENG Q. Application of integrated semigroups to higer order abstract Cauchy problem [J]. Systems Science&Mathematical Sciences, 1992, 5(4): 316-327.

[4] RALPH DELAUBENFELS.C-semigroups and strongly continuous semigroups [J]. Israel Journal of Mathematics, 1993, 1: 227-255.

[5] 郑权，雷岩松. 关于积分C半群[J]. 华中理工大学学报, 2000, 4(20): 181-187.

[6] 葛照强，朱广田，冯德兴. 广义算子半群与广义分布参数系统的适定性[J]. 中国科学:数学, 2010, 40(5): 477-495.

[7] JODER L, FEMANDEZ M L. An implicit difference methods for the numerical of solution of coupled system of partial differential equations [J]. Appl Math Comput, 1991, 46:127-134.

[8] LEWIS F L. A review of 2-D implicit systems [J]. Automatic, 1992, 28:345-354.

[9] HU Y, PENG S G, LI X J. Maximum principle for optimal control problem of nonlinear generalized systems-infinite dimensional case [J]. Acta Math Appl Sin, 1992, 15: 99-104.

[10] TRAZSKA Z, MARSZALEK W. Singular distributed parameter systems [J]. IEEE Control Theory Appl, 1993, 40:305-308.

[11] ADRENT W. Vector-valued Laplace transforms and Cauchy problems [J]. Israel J of Math, 1987, 59: 327-352.

[12] MARSHALL S. Asymptotic behavior ofC0-semigroups as determined by the spectrum of the generator [J]. Indiana University Mathematics Jouranl, 1976, 25(8): 782-793.

[13] ZHANG L P. Characteristic conditions for eventually normed continuous semigroup on a Hilbert space [J]. Acta Mathematica Sinica, 2003, 46(3): 439-444.

[14] SONG G Z. A problem of exponential stability for semigroups on Hilbert space [J]. Chinese Annals of Mathematics, 1992, 13A(5): 648-652.

[15] BENCHIMOL C D. Feedback stabilizability in Hilbert space [J]. Appl Math Optim,1978, 4: 225-248.