一种多级数据嵌入的信息隐藏方法研究

蔡龙飞，赵慧民

(1.广东工程职业技术学院，广东 广州 510520;2.广东技术师范学院,广东 广州 510665)

信息隐藏技术是实现保密通信和数字版权保护的一种有效方法，已成为多媒体信息安全研究领域持续发展的一个研究焦点。目前，基于小波变换的信息隐藏方法是实现信息隐藏的焦点技术[1-5]。

小波较 Fourier 分析更擅长的是表示局部奇异特征，但是严格采样的小波分析在表示多维信号时存在两大不足：变换不具备平移不变性；对具有方向性的几何奇异特征表示不稀疏。近年来，为了克服以上缺陷，同时保持小波多尺度分析和局部化时频分析能力，Daubechies[6], Vetterli[7], Mallat[8], Donoho[9]等国际权威小波研究专家提出了一系列全新的多尺度分析方法，由于这些方法和理论均具有小波的重要特征，我们称之为新型小波理论。

2000年，E Le Pennec和Stéphane ,Mallat提出了Bandelet变换[8]。Bandelet变换是一种基于边缘的图像表示方法，能自适应地跟踪图像的几何正则方向。Bandelet基并不是预先确定的,而是优化最终的应用结果来自适应的选择具体的基的组成。Pennec和Mallat给出了Bandelet变换的最优基快速寻找算法[8]。初步实验结果表明，与普通的小波变换相比，Bandelet变换在去噪和压缩方面体现出了一定的优势和潜力[10-11]，其压缩方法可以达到比JPEG2000 等主流方法更好的压缩效果。根据Bandelet变换的性质,文献[12]提出了一种基于Bandelet变换采用零水印思想的全频域无损水印算法,该算法检测了载体图像特征,但没有应用隐藏技术。文献[13]提出了基于第2代Bandelet变换的认证水印算法，利用了图像几何矢量线方向流特征，但该算法没有充分利用水印图像的边缘正则性和水印信息不同分布特性，因此，信息隐藏提取与认证精度有限。

目前，Bandelet变换通过自适应处理设计各向异性的基函数，建立了各向异性基函数字典，因此，可以实现对图像中的边缘进行稀疏表示。由于Bandelet变换具有边缘信息稀疏表示的能力，本文从一个新的角度来研究数字水印，即通过研究数字水印的边缘(特征信息)的稀疏表示，设计出一种对特征信息和一般信息采用不同隐藏策略的多级数据调制嵌入的数字水印算法，并建立了数字水印特征级检测和识别的数学模型，从而达到增加水印信息量，提高数字水印抗攻击能力和检测识别的准确性的目的。

1 Bandelet 理论及其应用的研究

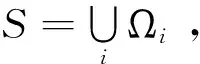
图1 JPEG, JPEG 2000, Bandelet三种变换编码思想图示Fig.1 Transform coding base principle of JPEG and JPEG 2000 as well as Bandelet

2 基于Bandelet的特征级数字图像水印算法

目前国内外鲜有应用Bandelet变换实现水印特征多级隐藏和检测的研究的报道。从对Bandelet变换的性质的介绍，我们知道其克服了经典小波变换的弊端(不具备平移不变性；对具有方向性的几何奇异特征表示不稀疏)。利用Bandelet变换对水印图像(尤其是数字指纹图像)几何边缘的稀疏表示能力，可以预见其应用于数字水印特征信息的提取和检测具有良好的性能。

2.1 基于Bandelet变换的图像几何特征条件分割

(1)

(2)

这样图像的统计形式就是一种Bandelet 变换模型。这种关系为把图像数据分割后局部和全局系数之间的几何特征统计关系提供了一个基本Bandelet 变换数据链。

2.2 基于Bandelet特征数据多级结构水印形式

根据Bandelet变换系数的不同分布及其不同重要性，本文提出一种基于Bandelet变换结构的多级数据调制嵌入的信息隐藏实现方法。这种多级结构是把相同空间位置和几何方向上的不同频率系数划分为同一组并构成一个“父-子”树结构的多级形式，它把数字水印图像特征点的不同数据按照Bandelet变换“父-子节点”关系的不同分解成不同能量的数字水印向量基，在多级结构的不同节点自适应生成不同强度的水印信息。

G={x1,x2,…,xn},xj∈{0,1},j∈N

(3)

E={e1,e2,…,en},ei=aj,

j·cr≤i≤(j+1)·cr,cr>1,i,j,cr∈N

(4)

Sk={k1,k2,…,kn},ki∈{0,1},i∈N

(5)

ai1,…,iL={m1,m2,…,mN-1},mi=ei·ki,i∈N

(6)

结合Bandelet变换分割和Bandelet变换树结构的多级数据调制嵌入，设信号X按照Bandelet变换几何特征分割进行统计，并实现了图像分割后，在Bandelet变换树中有N个可嵌入的子带系数，水印数据向量基{a}具有同样的长度和能量，则按照多级“父—子节点”的关系，在树的第i个节点上(即对应第i个子信道，1≤i≤L)嵌入的水印数据形式为：

(7)

Y(i)=αX(i)+W(i)

(8)

2.3 数字水印数据的多级调制嵌入与检测处理

这里，水印图像的几何特征数据呈现的状态X对编码而言是一种非因果关系，它由信源信息分布、攻击数据、和失真补偿组成。因此，按照2.2水印多级数据结构，本文采取的技术实现方案如图2,图3所示。对应的实现方案，数字水印嵌入过程如下。

图2 多级数据嵌入的信息隐藏实现方案(发送端)Fig.2 A information hiding scheme based multi-level data embedding at transmission

图3 多级水印数据恢复的信息隐藏实现方案(接收端)Fig.3 A information hiding scheme based multi-level data embedding at receiving

1)将待嵌入的水印图像进行Bandelet变换，得到一维不同子带的指纹数据和不同重要性的特征数据。

2)对载体图像S用多小波变换进行4级分解，对小波系数进行重排，并把相同空间位置和方向上的不同频率子带系数划分为同一组作为多小波树的“父—子节点”分支树。

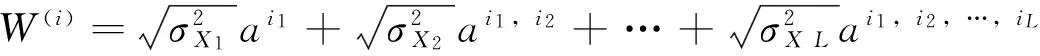
5)对嵌入水印数据后的多小波系数做反变换，得到含数字水印的混合图像。

对应图3的实现方案，数字水印检测与提取过程如下：

1)对含水印的混合图像用Bandelet变换进行4级分解，重排系数，得到Bandelet变换树及其分组。

2)对每个多级树结构的子带系数计算奇偶，提取嵌入的水印数据m。

3)相似度测量：用归一化相关系数定义如下：

(9)

如果η>T(设置的门限)，则指纹图像数据已经检测出来。显然，η越接近1越好。

3 实现结果及其性能分析

图4 Lena图像，指纹图像，混合图像和检测恢复的指纹图像Fig.4 Lena image，fingerprint image, stero-image and received fingerprint image(a)Lena载体图像, PSNR=38.37 dB;(b)指纹水印图像，PSNR=36.31 dB；(c) 多级嵌入后Lena图像, PSNR=35.28 dB; (d) 多小波变换嵌入图像, PSNR=34.69 dB; (e) Bandelet变换检测恢复的指纹; (f) 多小波变换检测恢复的指纹图像，PSNR=28.21 dB.

4 结 论

以Bandelet变换理论和算法研究为主线，本文从基于Bandelet变换的数字水印图像分割和几何信息特征描述表示出发，建立了一种有效的树结构多级水印数据分配模型。和基于小波变换的单级信息隐藏算法比较，实验结果说明了本文方法的有效性。未来，借鉴Bandelet变换的多级数据处理，我们将从指纹水印信息的特征提取、隐藏、检测等算法构造一种密钥密码实现技术，为数字水印的电子信息技术作为实际应用背景展开深入地研究。

参考文献：

[1] 赵耀.基于小波变换的抵抗几何攻击的鲁棒视频水印[J].中国科学E辑，2006, 36(2):137-152.

[2] EDWARD J, WONG P W, DITTMANN J, et al. Security, forensics, steganography, and watermarking of multimedia contents X (proceedings volume)[DB/OL].SPIE Digital Library, April 2008.

[3] VOLOSHYNOVSKIY S, PEREIRA S, PUN T. Attack modeling: Towards a second generation watermarking benchmark[J]. Signal Processing, Special Issue on Information Theoretic Issues in Digital Watermarking, June 2010,90(6): 1177-1214.

[4] 赵慧民，张惠乐，胡学骏. 一种基于树结构的高斯分布扩频指纹嵌入技术的方法研究[J]. 中山大学学报：自然科学版，2006，45(1):42-45.

[5] 赵慧民，康显桂，黄继武. Laplacian信源分割及其并行Gaussian信道传输的信息隐藏技术研究[J].中山大学学报：自然科学版,2008，47(4):29-34.

[6] DAUBECHIES I, HAN B, RON A,et al. Framelets: MRA based construction of wavelet frames[J]. Applied Comput Harmon Anal, 2004, 14(1):1-46.

[7] DO M N, VETTERLI M. Contourlets, beyond wavelets[C]. G V Welland ed, Academic Press, 2003.

[8] PENNEC E L, MALLAT S. Image compression with geometrical wavelets[C]. In Proc. of ICIP'2000.Vancouver, Canada, September, 2000: 661-664.

[9] DONOHO D, HUO X. Beamlets and multiscale image analysis, multiscale and multiresolution methods[J]. Springer Lecture Notes in Computational Science and Engineering, 2002(20):149-196.

[10] PENNEC E L, MALLAT S. Bandelet representations for image compression[C].Proceedings. 2001 International Conference on Volume 1,2001:12.

[11] PENNEC E L, MALLAT S. Sparse geometric image representations with bandelets[J]. IEEE Trans. Image Processing, 2005, 14(4):423-438.

[12] 杨岳湘，罗永，叶昭辉. 基于Bandelet与自适应矩阵范数的全频域无损水印方法[J].计算机研究与发展，2007，44(12)：1996-2003.

[13] 刘绪崇，罗永，王建新，等.基于第二代Bandelet变换的图像认证水印算法[J].通信学报，2010，31(12)：123-130.

[14] 赵慧民，郭一缜，丁晓艳. 一种数字图像和指纹水印位平面合成的优化方法[J].中山大学学报：自然科学版，2010,49(6)：64-67.