基于灰色关联分析的lasso法在区域用水经济效益系数中的应用*

屈国栋，楼章华，王 磊

(1.浙江大学水文与水资源工程研究所，浙江杭州 310058;2.浙江大学电气工程学院，浙江杭州 310027）

水资源优化配置是指在流域或特定区域内，通过工程或非工程措施对有限的水资源进行空间、时间上的调配，尽量满足各区域的用水需求，促进流域及区域经济的持续、稳定发展和生态环境的健康、稳定［1］。水资源可持续利用的基本手段之一就是水资源优化配置［2］，水资源优化配置是解决区域水资源短缺，提高用水经济和社会效益的重要和有效途径之一，而各用水户用水经济效益系数的确定则是优化配置的关键。当前，确定经济效益系数的方法主要有两种:直接确定法和层次分析法。直接确定法是通过分析经济效益系数的物理意义，利用现有的一些实际数据直接确定。例如:工业用水经济效益系数可取用水定额 (工业万元产值取水量)的倒数;农业灌溉用水经济效益系数按灌溉后的农业增产效益乘以水利分摊系数确定［3］。赵得军等［4］在水资源配置模型中，把不同形式水源的用水效益系数看作是时间的函数，利用遗传算法优化效益系数。沈军等［5］将水资源优化配置问题模拟为生物进化问题，通过遗传算法来求解经济效益系数。现有的方法都存在一些问题，如直接确定法虽然可以在一定程度上反映实际情况，但是由于需要确定的影响参数较多，量化比较困难，很难运用到模型求解中［6］。

本文在前人研究的基础上，首先运用灰色关联分析法的优势，初步确定影响经济效益系数的主要影响因子，然后根据历史用水数据，引入LASSO套索回归，作为量化的统计方法，对用水经济效益系数进行量化。

1 灰色关联分析法辨识经济效益系数影响因子

本文选用灰色关联分析方法，辨识影响因子，该方法是在灰色系统理论基础上的一种方法，可以分析系统中各个因素的关联程度。通过各因子的关联度比较，可以确定出主次因素，得出影响某变量的主要因子。

灰色关联分析的基本思想是根据序列曲线几何形状的相似程度来判断其联系是否紧密，曲线越接近，相应序列之间的关联度就越大，反之就越小［7］。

各影响因子与需水量的关联系数与关联度计算公式如下［8］。

关联系数￡:

其中:XO(k)和Xi(k)，k=1，2，… ，n，i=1，2，…，m，分别为各个用水部门的用水量时间序列和相应的影响因子时间序列。ρ为分辨系数，值处于0～1之间，通常取0.5。

2 lasso方法介绍

LASSO套索估计方法用于逼近线形模型，LASSO最小化受约束的残留平方和误差，由于这一约束的本质特性，LASSO可以使得一些系数严格为零，从而能够给出可解释的模型［9］。Volker［10］提出了一个称为广义LASSO的稀疏核回归模型，它是LASSO方法的非线性形式。由于解的极度稀疏性，广义LASSO的性能优于支持向量机。

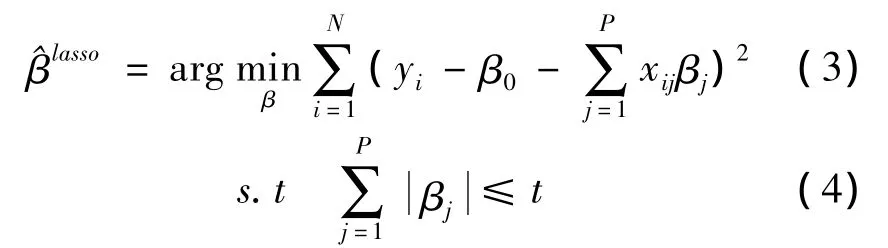
其中，yi是归一化的目标函数真实值，β0是线性分类函数的截距。L1套索罚的约束使得解在yi上为非线性，并使用二次规划来计算它们［11］。由于该约束的特征，使得t充分小将导致某些系数恰好为0。这样，套索做了某种连续的子集选择。通过自适应的选择t，极小化期望预测误差估计，得到βj的估计。

3 基于灰色关联分析的lasso法求解经济效益系数

3.1 研究区域概况

周口市位于河南省东南部，面积1.19万km2，耕地82.6万hm2，人口1090万人。辖八县一市一区和一个省级经济开发区。周口地势平坦，土地肥沃，是国家重要的粮、棉、油、肉、蛋、奶生产基地，有“中原粮仓”之称;2010年粮食产量达72.35亿kg，居河南省第一位。周口市多年平均水资源总量为26.10亿m3。全市人均水资源量244 m3，为河南省人均水资源量500 m3的48.8%;亩均水资源量204 m3，为全省亩均水资源量395 m3的51.6%。周口市属于水资源严重缺乏地区。

近年来，由于加快中原经济区建设，城市化进程不断推进，周口市水资源短缺问题日益显现，加之水污染和水环境问题的加剧，尤其是水质性缺水问题引人注目。由水资源而引发的各种问题，对经济发展的约束已经凸显，水资源的数量和质量已经难以承载当地经济社会的可持续发展。因此，准确的量化用水经济效益系数，实现合理的配置有限的水资源，势在必行。

本文根据行政区域，将周口市十个县市分为十个子区，根据《周口市水资源公报》、《周口市统计年鉴》等资料得到相关数据，运用各子区2010年的实际用水情况等数据，对所建模型进行拟合，确定出周口市各子区工业、农业用水的经济效益系数。

3.2 基于灰色关联分析的lasso法经济效益系数求解

3.2.1 经济效益系数影响因子灰色关联分析法辨识 分析研究区域实际用水状况，首先定性确定经济效益系数影响因子，依据实际数据，按照前文所述灰色关联分析方法，分别求出各用水部门的实际用水经济效益与各影响因子的关联系数，进一步计算出关联度。通过关联度的排序可初步确定主要影响因子。得出周口市各用水部门实际用水经济效益主要影响因子如表1所示。可初步确定与经济效益系数关联性较高的因子。

表1 周口市各用水部门经济效益系数影响因子灰色关联分析法计算结果Table 1 Results of effecting factors identified by gray relational analysis method foreconomic efficiency coefficient of Zhoukou

3.2.2 基于lasso的经济效益系数求解 在运用灰色关联分析法初步确定各子区各部门用水经济效益系数的主要影响因子后，分析周口市工业、农业两个用水部门的数据，引入LASSO套索估计，分别量化每个部门中的各子项的效益系数。以每个行业中总体经济指标为标准，计算出各个影响因素的效益系数。

其中，Y为总体经济指标，Ej是影响因素，ki是效益系数，L0为截距。使用Matlab(The MathWorks，Inc.R2009b)，利用开源软件包 glmnet package，实现了凸优化方法自适应估计Ki，具体算法参见Koh K 等的文献［12］。

根据《周口市统计年鉴》、《周口市水资源公报》等资料，进行数据的初步统计分析，得到2010年周口市各行政分区工业、农业经济效益系数主要影响因子的值如表2、3所示。

运用前述理论，对表2、3中的数据，以工业总产值和农业总产值为总体经济指标，用lasso回归分析，得到线性回归函数:

表2 2010年周口市各行政分区工业经济效益系数主要影响因子值Table 2 The effecting factors value of industrial economic efficiency coefficient of Zhoukou in the year 2010

表3 2010年周口市各行政分区农业经济效益系数主要影响因子值Table 3 The effecting factors value of agricultural economic efficiency coefficient of Zhoukou in the year 2010

由式 (6)、(7)可知，在以工业、农业总产值最大为目标的情况下，影响总产值最大的影响因子及其值如表4所示。

表4 2010年周口市工业、农业用水经济效益影响因子及其系数值Table 4 The effecting factors of industrial and agricultural water use economic efficiency coefficient and the coefficient of Zhoukou in the year 2010

由表4可知，工业用水方面，对工业总产值影响较大的有火电用水量和地下水用水量，因此，为了提高工业用水经济效益，可以通过提高火电用水量，增加工业用水中地下水的比例，以此提高工业用水经济效益。农业用水方面，对农业总产值影响较大的是菜田用水量和农田灌溉用水量，可以通过适当增加菜田种植面积，以及在可能的情况下，通过提高农田灌溉用水量来增加农业用水经济效益。根据表4中的影响因子及其系数值，可对区域合理的利用水资源提供参考，为水资源的合理配置提供对策和建议。

4 结语

本文运用灰色相关分析方法，初步分析区域用水经济效益系数的主要影响因子，然后运用lasso方法求解，以区域总产值最大作为目标，综合考虑各个县市的用水收益情况，得出各影响因素的效益系数，这些效益系数可以作为当年和时间较临近的年份的参考依据。其他年份的数据采用本文中的方法，可以得到相应的效益系数集合。因为每年的效益系数是动态变化的，所以采用本文中的方法能够动态地计算每年的效益系数，再据此做进一步的优化。本文为水资源优化配置模型中经济效益系数的确定提供了一种更加精确和量化的方法。为区域水资源管理和水资源的合理配置提供了依据。

［1］孙志林，夏珊珊，许丹，等.区域水资源的优化配置模型［J］.浙江大学学报:工学版，2009，43(2):344－348.

［2］王海政，仝允恒.可持续发展视角下的区域水资源优化配置模型［J］.清华大学学报:自然科学版，2007，47(9):1531－1536

［3］冯耀龙，韩文秀，王宏江，等.面向可持续发展的区域水资源优化配置研究［J］.系统工程理论与实践，2003(2):133－138.

［4］赵得军，洪 林，李远华，等.效益系数年际动态变化的水资源合理配置［J］.中国农村水利水电，2004，22(9):34－36.

［5］沈军，刘勇键.水资源优化配置模型参数识别的遗传算法［J］.武汉大学学报:工学版，2002，35(3):13 －16.

［6］陈夺峰，黄岁樑.改进遗传算法确定水资源优化配置模型经济效益系数［J］.水资源保护，2008，24(2):6 －9.

［7］刘思峰，党耀国，方志耕等.灰色系统理论及其应用［M］.北京:科学出版社，2005.

［8］王艳菊，王珏，吴泽宁.基于灰色关联分析的支持向量机需水预测研究［J］.节水灌溉，2010，10(4):49 －52.

［9］TIBSHIRANI，R.Regression shrinkage and selection via the lasso［J］.Jounal of the Royal Statistical Society.1996，58(1):267 －288.

［10］VOLKER R.The generalized LASSO［J］.IEEE Transactions on Neural Networks，2004，15(1):16 －28.

［11］李霞，刘超.基于收缩机制的若干回归模型比较研究［J］.统计与决策，2008，5:30－32.

［12］KOH K，KIM S J，BOYD S.An interior-point method for large-scale L1-regularized logistic regression［J］.Journal of Machine Learning，2007(8):1519－1555.